Bei­spie­le für Übungs­auf­ga­ben in Sto­chas­tik

Ver­tieft ver­ständ­nis­ori­en­tier­te Übungs­auf­ga­ben aus der Sto­chas­tik

Auf­ga­be 1

Ge­ge­ben sind die An­tei­le drei­er Typen von PKW unter den Neu­zu­las­sun­gen in einem Land in den Jah­ren 2018, 2019 und 2020.​Im Jahr 2018 wur­den in die­sem Land 300 000 PKW neu zu­ge­las­sen.

1. In einer Zei­tung steht fol­gen­de Aus­sa­ge: „Der An­teil der neu­zu­ge­las­se­nen Die­sel- PKW in den Jah­ren 2018 und 2019 ins­ge­samt ist grö­ßer als der An­teil der neuzu ge­las­se­nen Ben­zin- PKW im glei­chen Zeit­raum.“ Ent­schei­den Sie ob, diese Aus­sa­ge wahr sein kann und be­grün­den Sie ihre Ent­schei­dung.
2. Be­stim­men Sie die Min­dest­an­zahl an PKW, die in die­sem Land im Jahr 2019 neu zu­ge­las­sen wor­den sind, wenn die Aus­sa­ge aus a) falsch ist.
3. Im Jahr 2019 wur­den in die­sem Land 240 000 PKW neu zu­ge­las­sen. Der An­teil der Elek­tro/Hy­brid- PKW die ins­ge­samt in den drei Jah­ren neu zu­ge­las­sen wor­den sind be­trägt 12%. Be­stim­men Sie den pro­zen­tua­len An­stieg der An­zahl der Elek­tro/Hy­brid- PKW vom Jahr 2019 zum Jahr 2020.

Auf­ga­be 2

Um nach­zu­wei­sen, ob eine Per­son eine be­stimm­te Krank­heit hat, wurde ein Test ent­wi­ckelt. Die Wahr­schein­lich­keit, dass eine tat­säch­lich in­fi­zier­te Per­son auch vom Test als in­fi­zier­te Per­son er­kannt wird (Test: po­si­tiv) be­trägt 99%.Die Wahr­schein­lich­keit, dass eine tat­säch­lich nicht in­fi­zier­te Per­son auch vom Test als nicht in­fi­zier­te Per­son er­kannt wird (Test: ne­ga­tiv) be­trägt 98%.

1. In einem Land sind 5% der Ein­woh­ner in­fi­ziert (In­fi­zier­ten­ra­te). Be­stim­men sie die Wahr­schein­lich­keit, dass eine ne­ga­tiv ge­tes­te­te Per­son tat­säch­lich nicht in­fi­ziert ist.
2. In einem an­de­ren Land be­trägt die Wahr­schein­lich­keit, dass eine po­si­tiv ge­tes­te­te Per­son tat­säch­lich in­fi­ziert ist, 50%. Be­stim­men Sie die In­fi­zier­ten­ra­te in die­sem Land.

Auf­ga­be 3

In einem Vol­ley­ball­ver­ein sind die Spie­ler in drei Grup­pen ein­ge­teilt wor­den. Die Durch­schnitts­grö­ße der Spie­ler in Grup­pe A be­träg­t1,98 m, in der Grup­pe B 1,92 m.

1. Falls ein Spie­ler X aus Grup­pe A in die Grup­pe B wech­selt dann steigt in bei­den Grup­pen die Durch­schnitts­grö­ße der Spie­ler. Geben Sie an, wie groß die­ser Spie­ler sein kann
2. Die Durch­schnitts­grö­ße in der Grup­pe C be­trägt auf Zen­ti­me­ter ge­run­det 1,97 m. Ein Spie­ler Y mit der Größe 2,05 m kommt neu in diese Grup­pe. Da­durch än­dert sich die auf Zen­ti­me­ter ge­run­de­te Durch­schnitts­grö­ße nicht. Be­stim­men Sie die Min­dest­an­zahl der Mit­glie­der in Grup­pe C, bevor die­ser Spie­ler Y hin­zu­kam.

Auf­ga­be 4

Ein Kar­ten­spiel be­steht aus Kar­ten der vier Far­ben blau, rot, grün und oran­ge. Von jeder Farbe gibt es genau 20 Kar­ten, von denen jede genau mit einer Zahl von 1 bis 20 be­schrif­tet ist. In jeder Farbe kommt dabei jede Zahl genau ein­mal vor.

a) Aus die­sem Kar­ten­spiel wer­den zu­fäl­lig drei Kar­ten mit einem Griff ge­zo­gen. Be­stim­men Sie je­weils die An­zahl der Mög­lich­kei­ten für fol­gen­de Er­eig­nis­se:

A: Die drei Kar­ten haben alle eine ver­schie­de­ne Farbe.

B: Alle drei Zah­len sind gleich.

C: Man er­hält drei Kar­ten einer Farbe, deren Zah­len un­mit­tel­bar auf­ein­an­der

fol­gen (Drei­er­se­quenz: z.B. 6 ; 7 ; 8)

b) Ein Spiel wird mit vier Spie­lern ge­spielt. Jeder Spie­ler er­hält dabei alle 20 Kar­ten einer Farbe. In jeder Spiel­run­de wählt jeder Spie­ler genau eine Karte zu­fäl­lig aus und legt diese auf Tisch. Sind alle vier Zah­len ver­schie­den, dann ge­winnt der Spie­ler mit der höchs­ten Zahl diese Runde. Kommt eine Zahl mehr­fach vor, dann ge­winnt nie­mand diese Runde. Be­rech­nen Sie die Wahr­schein­lich­keit, dass je­mand die erste Runde ge­winnt.

c) Das Spiel wird ab­ge­bro­chen, so­bald eine Spiel­run­de kei­nen Ge­win­ner hat. Sei X die An­zahl der Spiel­run­den, die einen Ge­win­ner hat. Geben Sie eine mög­li­che Kar­ten­fol­ge an, damit X = 20 gilt.

d) Jetzt wählt nur der Spie­ler mit den roten Kar­ten seine Kar­ten zu­fäl­lig aus und legt sie nach­ein­an­der auf den Tisch bis eine Se­quenz un­ter­bro­chen wird.

Bei­spie­le: 12; 13; 14; 8 (Drei­er­se­quenz)

3; 4; 5; 6; 7; 8; 17 (Sech­ser­se­quenz)

Be­stim­men Sie die An­zahl aller Mög­lich­kei­ten eine Fün­fer­se­quenz zu er­hal­ten.

Auf­ga­be 5

Ein Pa­lin­drom ist eine na­tür­li­che Zahl, die ihren Wert nicht än­dert, wenn man ihrer Zif­fern in um­ge­kehr­ter Rei­hen­fol­ge auf­schreibt. (Bei­spiel: 2 772)

a) Be­stim­men Sie so­wohl die An­zahl aller drei­stel­li­gen als auch die An­zahl aller vier­stel­li­gen Pa­lin­dro­me.

b) Ein Zu­falls­ge­ne­ra­tor lie­fert jede der Zif­fern 0 bis 9 mit der glei­chen Wahr­schein­lich­keit. Mit Hilfe die­ses Zu­falls­ge­ne­ra­tors wer­den vier­stel­li­ge Zah­len er­zeugt. Dabei wird zu­erst die Füh­rungs­zif­fer der Zahl so zu­fäl­lig er­zeugt, dass die Zif­fern 1 bis 9 je­weils mit der glei­chen Wahr­schein­lich­keit auf­tre­ten. Be­stim­men Sie die Wahr­schein­lich­keit dafür, dass die vier­stel­li­ge Zahl ein Pa­lin­drom ist.

c) Sei n eine un­ge­ra­de na­tür­li­che Zahl. Be­grün­den Sie, dass die Wahr­schein­lich­keit mit dem Zu­falls­ge­ne­ra­tor ein Pa­lin­drom mit n Stel­len zu er­hal­ten, grö­ßer ist als die Wahr­schein­lich­keit ein Pa­lin­drom mit n + 1 Stel­len zu er­hal­ten.

d) Die Wahr­schein­lich­keit mit dem Zu­falls­ge­ne­ra­tor ein Pa­lin­drom mit n Stel­len zu er­hal­ten be­trägt

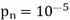
Geben Sie an wel­che Werte für n in Frage kom­men.

e) Be­stim­men Sie die An­zahl der fünf­stel­li­gen Pa­lin­dro­me, bei denen die ers­ten drei Zif­fern ver­schie­den von­ein­an­der sind.

f) Be­stim­men Sie die An­zahl der sechs­stel­li­gen Pa­lin­dro­me, die nur ge­ra­de Zif­fern be­sit­zen, wobei die ers­ten bei­den Zif­fern ver­schie­den von­ein­an­der sind.

g) Be­stim­men Sie die An­zahl der sie­ben­stel­li­gen Pa­lin­dro­me, deren ers­ten drei Zif­fern eine an­stei­gen­de Se­quenz di­rekt auf­ein­an­der fol­gen­der Zif­fern sind.

(Bei­spiel: 3 451 543)

h) Be­grün­den Sie, dass es keine sechs­stel­li­gen Pa­lin­dro­me mit der Quer­sum­me 21

gibt.

i) Be­stim­men Sie die An­zahl der fünf­stel­li­gen Pa­lin­dro­me mit der Quer­sum­me 13.

Auf­ga­be 6

Ge­ge­ben sind zwei Urnen A und B. 20 rote und 20 weiße Ku­geln wer­den zu­fäl­lig auf die bei­den Urnen so ver­teilt, dass sich am Ende in bei­den Urnen je­weils 20 Ku­geln be­fin­den.

Immer wenn aus der Urne A eine Kugel ge­zo­gen wird, dann wird diese so­fort in die Urne B ge­legt. Immer wenn man eine Kugel aus der Urne B zieht, dann wird diese so­fort in die Urne A ge­legt.

1. Be­stim­men Sie die An­zahl der Mög­lich­kei­ten die 40 Ku­geln auf die bei­den Urnen zu ver­tei­len.
2. Die Wahr­schein­lich­keit beim ers­ten Zug aus Urne A eine rote Kugel zu zie­hen be­trägt 40%. Be­stim­men Sie je­weils die An­zah­len der je­wei­li­gen Ku­gel­far­ben in den bei­den Urnen bevor zum ers­ten Mal ge­zo­gen wird.
3. Sei X die An­zahl der roten Ku­geln zu Be­ginn in der Urne A. Man zieht nach­ein ander aus bei­den Urnen, wie oben be­schrie­ben, zu­fäl­lig je eine Kugel. Ge­ge­ben ist das Er­eig­nis E:“ Beide Ku­geln haben die glei­chen Farbe.“ Be­stim­men Sie die Wahr­schein­lich­keit von E in Ab­hän­gig­keit von X.
4. Zei­gen Sie, dass diese Wahr­schein­lich­keits­ver­tei­lung be­züg­lich X sym­me­trisch ist.
5. Jetzt gilt X = 10. Es wird, wie oben be­schrie­ben, zu­nächst aus Urne A, dann aus Urne B, dann er­neut aus Urne A und zu­letzt aus Urne B zu­fäl­lig eine Kugel ge­zo­gen. Be­stim­men Sie die Wahr­schein­lich­keit, dass sich an­schlie­ßend in bei­den Urnen er­neut je­weils 10 rote Ku­geln be­fin­den.