Be­we­gung einer Pleu­el­stan­ge

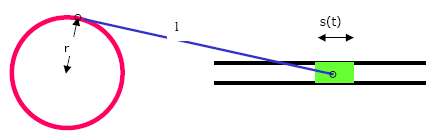
Zei­gen Sie, dass für die Weg-Zeit-Funk­ti­on des Kol­bens gilt:

Er­gän­zen Sie die Funk­ti­ons­glei­chung.
Geben Sie die Funk­ti­on s(t) in das CA-Sys­tem ein. (r=5, l=20)

Be­rech­nen Sie mit Hilfe des CAS dar­aus die

• Ge­schwin­dig­keits-Zeit – Funk­ti­on und die
• Be­schleu­ni­gungs-Zeit - Funk­ti­on

Zeich­nen Sie die drei Schau­bil­der mit dem CAS.

Die Ab­wei­chun­gen von der Si­nus­form wer­den im Ge­schwin­dig­keits-Zeit- Dia­gramm deut­lich, noch deut­li­cher im Be­schleu­ni­gungs-Zeit-Dia­gramm.

Ver­än­dern Sie das Ver­hält­nis von Ra­di­us zu Länge der Stan­ge (z.B. r=5, l= 12) und be­ob­ach­ten Sie die Ver­än­de­run­gen.

Be­schrei­bung

An die­ser Sta­ti­on sol­len Schü­le­rIn­nen

• er­fah­ren, wie man mit CAS Ab­lei­tungs­funk­tio­nen be­stim­men und zeich­nen kann.
• wel­che Zu­sam­men­hän­ge zwi­schen Funk­tio­nen und Ab­lei­tungs­funk­tio­nen be­ste­hen.
• wel­che Be­deu­tung Funk­ti­ons­wer­te, Ab­lei­tungs­wer­te in einem an­wen­dungs­be­zo­ge­nen Bei­spiel haben.
• dass Ab­lei­tungs­funk­tio­nen sehr sen­si­bel ge­gen­über klei­nen Än­de­run­gen in der Funk­ti­on sind.
• dass beim Dif­fe­ren­zie­ren „Schwan­kun­gen“ der Funk­ti­on deut­lich her­vor­tre­ten, wäh­rend beim In­te­grie­ren „Schwan­kun­gen“ ge­glät­tet wer­den.

• „Dif­fe­ren­zie­ren“ -	„Un­ter­schie­de her­vor­he­ben“
  „In­te­grie­ren“ -	„Un­ter­schie­de auf­he­ben“

  sprach­lich:
  

Ar­beits­auf­trag

1. Ver­set­zen Sie Sich in die Schü­ler­rol­le und be­ar­bei­ten Sie das Ar­beits­blatt „Be­we­gung einer Pleu­el­stan­ge“.

2. Im Maple-works­heet „pleu­el­stan­ge.mw“ müs­sen Sie – im Ge­gen­satz zu den Schü­lern die Ein­ga­ben mit ENTER be­stä­ti­gen.
   Zur Ver­än­de­rung der Länge der Pleu­el­stan­ge än­dern Sie bitte im works­heet die Zeile 3.

3. Be­trach­ten Sie das App­let „lan­ge_kur­ze_­Pleu­el­stan­ge.swf“.
   http://​www.​invo.​fh-​kon­stanz.​de/​flash/​lan­ge_​kur­ze_​ple​uels​tang​e.​swf