Achill und die Schildkröte

Der Philosoph Zenon von Elea (495-430 v. Chr.) behauptete, dass Achill, der
schnellste Läufer der Griechen eine Schildkröte niemals überholen
könnte, wenn diese eine Vorsprung von 100 Fuss bekommt.
Was meinst Du zu dieser Behauptung?
| Achill: | Ha, lächerlich, 100 Fuss bin ich Null Komm Nichts gelaufen. |
| Schildkröte: | Dein Problem besteht darin, dass du diese Strecke eben nicht in Null Komma Nichts schaffst, sondern auch Zeit brauchst und in dieser Zeit bin ich auch ein Stück vorangekommen nämlich 10 Fuss. |
| Achill: | Pah, 10 Fuss, gar nichts. |
| Schildkröte: | Nicht sofort, auch dafür brauchst Du Zeit und in dieser Zeit bin ich wieder ein Stückchen weiter, nämlich 1 Fuss. |
|
Und so weiter und so weiter und so weiter und so weiter und
so weiter und so weiter und so
... |
Was meist Du zur Argumentation der Schildkröte?
Übersetzen wir die Sache in die Sprache der Mathematik: Die Strecke setzt
sich aus immer kleiner werdenden Teilstrecken zusammen.
![]() .
.
Wir wollen uns dem Problem anhand eines Blatt Papiers nähern:
Nimm zwei Blätter Papier. Falte eines in der Mitte und reiße es an
der Faltlinie auseinander.
Lege eine Hälfte auf den Tisch und halbiere die andere Hälfte wieder.
Lege wiederum eine Hälfte auf den Tisch und halbiere die andere.
Fahre solange damit fort, bis Du nicht mehr halbieren kannst.
Übersetze Dein Vorgehen in die Sprache der Mathematik.
Wenn Du nun alle Rechtecke aus Papier zusammen auf den Tisch legst, was kannst Du dann über die Anzahl der Blätter sagen?
Was würde geschehen, wenn wir technisch in der Lage wären, die Blätter unendlich oft zu teilen und anschließend aufsummieren?
Was würdest Du der Schildkröte nun als Argument entgegensetzen.
Erstell in Excel eine Tabelle:
Tipp: In der ersten Spalte multiplizierst Du immer mit dem entsprechenden Faktor,
in der zweiten addierst Du auf.
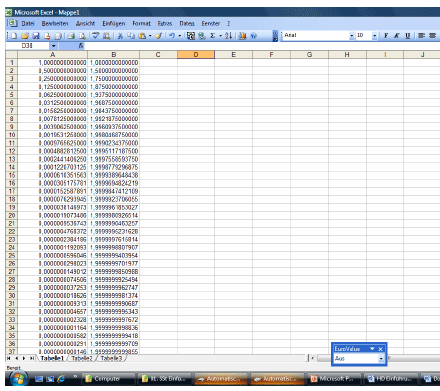
Nach welcher Strecke holt Achill die Schildkröte ein?
