Origami: Flächenformeln beweisen
Flächeninhaltsformel eines Dreiecks mit Origami
Hinweise für die Lehrkraft
Anhand dieses Arbeitsblatts erarbeiten die Schülerinnen und Schüler mit Hilfe von Origami die Flächeninhaltsformel für Dreiecke. Der haptische Zugang fördert das Verständnis für die Formel.
Neben der Umsetzung von Text trainieren die Schülerinnen und Schüler das räumliche Vorstellungsvermögen. Außerdem bereitet diese Übung auf die Beweise von weiteren Flächenformeln mit Hilfe von Origami vor, wie die von Parallelogramm, Trapez, Raute oder Drache.
Um die Schülerinnen und Schüler auf diese Art der Flächenbeweise einzustimmen, eignen sich sehr gut die Aufgaben der Kopfgeometrie aus den Handreichungen für die Klasse 8:
lehrerfortbildung-bw.de/u_matnatech/mathematik/bs/6bg/6bg1/6geometrie/1kopfgeometrie/
Vorbereitung
Die Schülerinnen und Schüler brauchen ein A4-Blatt und eine Schere. Sie teilen das Papier in vier A6-Blätter, mit denen im Anschluss weitergearbeitet wird.
Flächeninhaltsformel eines Dreiecks mit Origami
-
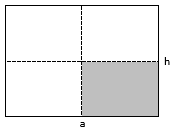 Nimm ein Blatt im Format A6. Es stellt ein Rechteck mit den Seiten a und h dar. Der Flächeninhalt dieses Rechtecks ist
A
1
=a*h.
Nimm ein Blatt im Format A6. Es stellt ein Rechteck mit den Seiten a und h dar. Der Flächeninhalt dieses Rechtecks ist
A
1
=a*h.
- Falte das A6-Blatt einmal entlang einer Mittellinie. Wie groß ist das Rechteck jetzt? Drücke den Flächeninhalt A 2 mit Hilfe von a und h aus.
- Gib den Flächeninhalt A 3 des Rechtecks an, das entsteht, wenn du das Rechteck aus 2. ein weiteres Mal entlang der anderen Mittellinie des Ausgangsblatts faltest. a
-
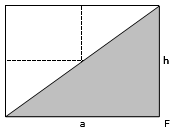 Nimm ein zweites A6-Blatt und falte es diagonal. Du erhältst zwei Dreiecke. Schneide eines dieser Dreiecke ab. Drehe das andere Dreieck so wie das graue Dreieck in der Abbildung nebenan und markiere die Seiten mit a und h.
Nimm ein zweites A6-Blatt und falte es diagonal. Du erhältst zwei Dreiecke. Schneide eines dieser Dreiecke ab. Drehe das andere Dreieck so wie das graue Dreieck in der Abbildung nebenan und markiere die Seiten mit a und h.
Falte nun die beiden Ecken auf die Ecke F (F ist Fußpunkt der Höhe). Das gefaltete Dreieck sieht dann wie folgt aus:
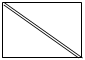 Vergleiche den Flächeninhalt des gefalteten Dreiecks mit dem Flächeninhalt des Rechtecks aus Nr. 3. Erkläre anhand deiner Faltfigur, warum der Flächeninhalt des Dreiecks
Vergleiche den Flächeninhalt des gefalteten Dreiecks mit dem Flächeninhalt des Rechtecks aus Nr. 3. Erkläre anhand deiner Faltfigur, warum der Flächeninhalt des Dreiecks
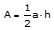 ist.
ist.
-
Nimm ein neues A6-Blatt und schneide ein Dreieck aus, das nicht rechtwinklig ist.
Die Höhe h und die Grundseite a
sollen
gleich lang sein wie oben.
Bestimme die Lage der Höhe durch Falten und lege das Blatt wieder auseinander. Falte nun die Ecke, bei der die Höhe endet, auf den Fußpunkt der Höhe. Falte die anderen beiden Ecken auch zu dem Fußpunkt der Höhe.
Wie groß ist die Fläche des gefalteten Dreiecks? Welche Folgerung ergibt sich daraus für den Flächeninhalt eines beliebigen Dreiecks?
- Schneide jeweils ein Parallelogramm, ein Trapez, eine Raute, einen Drachen aus und versuche mit Hilfe des geschickten Faltens zu einem Rechteck, bei dem das Papier überall doppelt liegt, die Flächenformeln zu entdecken bzw. zu begründen.
Flächeninhaltsformel eines Dreiecks mit Origami

703_p_flaecheninhaltsformel_ab_origami_de
Herunterladen
[doc] [125 KB]
703_p_flaecheninhaltsformel_ab_origami_de
Herunterladen
[pdf] [37 KB]
