Lehrplaneinheit (LPE) 4 Funktionen und ihre Schaubilder, zugehörige Gleichungen
Wiederholung der Mittelstufenthemen
-
der Funktionsbegriff
- war Wahlthema oder
- wird neu eingeführt
-
Gerade und Parabel nach dem Stand der Mittelstufe
- wiederholen
- festigen
Hauptziel
- Themenvertiefung zur Erleichterung des Übergangs in das 1BKFH
Weitere Ziele
-
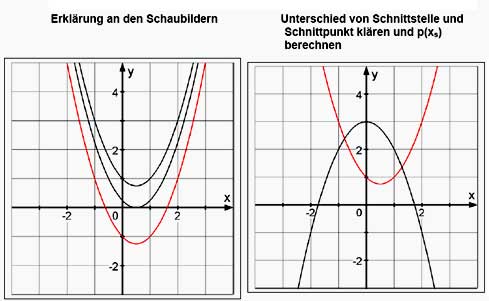
An Alltagsbeispielen, Grafiken, Wertetabellen und Textaufgaben wird der
Funktionsbegriff und das Schaubild K eingeführt.
Für viele Schüler ist die Funktionsschreibweise (siehe LP) unbekannt und bedarf einiger Übung. -
Die Sprache in der Mathematik hat in LPE 4 einen hohen Stellenwert.
Beispiele aus dem Berufsalltag führen die Schüler/innen zu Kostenfunktionen oder Bewegungsgesetzen. - Die verschiedenen Darstellungsmöglichkeiten von Funktionen wie Grafiken, Wertetabellen, Schaubild K der Funktion f sollen ausführlich geübt werden.
Funktionen und ihre Darstellung
| durch eine Wertetabelle |
|
| durch eine Gleichung |
|
| Schreibweise : |
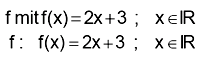
|
| K ist das Schaubild von |
|
-
durch ein Schaubild
-
 durch
die Sprache
durch
die Sprache
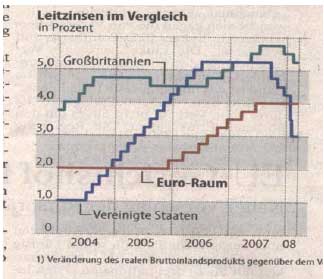
Das neben skizzierte Diagramm zeigt die Entwicklung der Leitzinsen in verschieden Regionen. Demzufolge blieb der Leitzins im Euroraum bis Mitte des Jahres 2005 konstant bei 2,0 % und stieg dann gleichmäßig bis Mitte des Jahres 2007 an auf 4,0 %, um auf diesem Wert konstant zu bleiben. Beschreiben Sie die Entwicklung der Leitzinsen für die Vereinigten Staaten und Großbritannien .
Lineare Gleichungen (LPE 4 S.7) integrativ
Beispiel.: Für
![]() sind die Funktionen g, h, k gegeben durch:
sind die Funktionen g, h, k gegeben durch:
h : h ( x ) = 2/3 x + 2
k : k ( x ) = - 2 x - 3
g : g ( x ) = - 2 x + 1
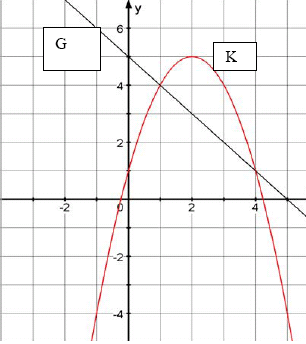
G, H, K sind die Schaubilder der Funktionen
Lösung:
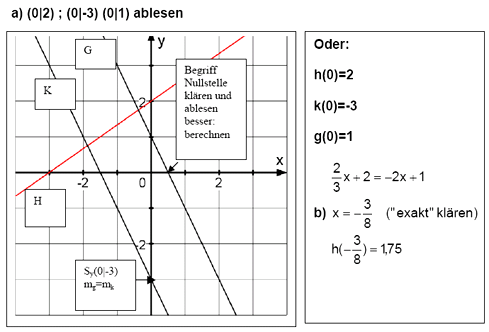
c) Die Schaubilder sind parallel / Steigung der Geraden ist gleich, damit
besitzen G und K keinen gemeinsamen Punkt .
- 2x - 3 = -2x +1
- 3 = +1 falsche Aussage
quadratische Gleichungen (LPE 4 S.8) integrativ
Beispiel:

-
Welche der Funktionen besitzt zwei, eine oder keine Nullstelle(n)?
Berechnen Sie die Nullstellen. -
Für
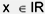 ist die Funktion p gegeben durch: p : p(x) = -x^2 + 3
ist die Funktion p gegeben durch: p : p(x) = -x^2 + 3
Ihr Schaubild ist P. Berechnen Sie die Schnittpunkte von P und F 1 .
Lösung: quadratischen Gleichungen lösen .......