Massendefekt: Lösung
Die Leistung der Sonne pro m² nennt man Solarkonstante S0, sie ist abstandsabhängig und beträgt im Erdabstand S0 = 1367 W/m².

Einstein hat mit seinem Energie-Masse-Äquivalent (E = mc²; c: Lichtgeschwindigkeit) gezeigt, dass Masse in Energie umgewandelt werden kann und damit erst die Prozesse im Sonneninneren verstehbar gemacht. Im Sonnenkern findet bei der Kernfusion von Wasserstoff- zu Heliumkernen die Umwandlung von Masse in Energie statt.
(1) Berechnen Sie mithilfe der Solarkonstanten die Masse, die im Sonneninneren in jeder Sekunde in Energie umgewandelt wird und damit den sekündlichen Massenverlust der Sonne.
Die Oberfläche der gedachten Kugel mit dem Radius r = 1AE beträgt:
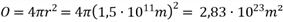
Die Gesamtleistung der Sonne beträgt also (das entspricht der Leistung durch die Gesamtfläche):
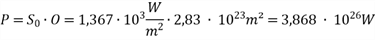
Nach Einstein gilt also mit E = mc² für die in Energie umgewandelte Masse in jeder Sekunde:
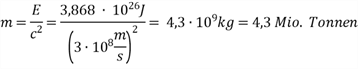
(2) Die Sonne hat zur Zeit eine Masse von 1,9889 ∙ 1030 kg.
Die Sonne beendet ihr Dasein in etwa 5 Mrd. Jahren.
Berechnen Sie das Verhältnis der bis dahin in Energie umgewandelten Masse zur Sonnenmasse unter Annahme, dass der Fusionsprozess konstant bleibt.
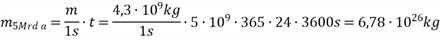
Für das Verhältnis gilt also:
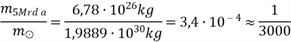
Massendefekt: Lösung: Herunterladen [docx][101 KB]
Massendefekt: Lösung: Herunterladen [pdf][123 KB]
Weiter zu Schwarzschildradius
