Zur Hauptnavigation springen [Alt]+[0] Zum Seiteninhalt springen [Alt]+[1]

GeoGebra: Bestimmen der Kreiszahl

Bestimmung der Kreiszahl π – GeoGebra 1

Hinweis für die Lehrkraft

Archimedes errechnete 260 v. Chr. für die Kreiszahl  die Abschätzung

Formel 1 .

Hierzu fügte er ein regelmäßiges 96-Eck in einen Kreis mit Radius r = 1 ein und berechnete dessen Flächeninhalt.

Die Schülerinnen und Schüler vollziehen dies mithilfe von GeoGebra und dem Programm Kreisberechnung_Exhaustion_3.ggb (siehe Bild unten) nach.

GeoGebra, eine dynamische Geometriesoftware, kann für nicht kommerzielle Zwecke kostenlos genutzt werden und ist über www.geogebra.org/cms/de/ erhältlich.

Vorgehensweise

Kreiszahl

An den PCs wird GeoGebra gestartet und das Programm
Kreisberechnung_Exhaustion_3.ggb geladen.

Die Funktionen der Software werden mit den Schülerinnen und Schülern besprochen. 2

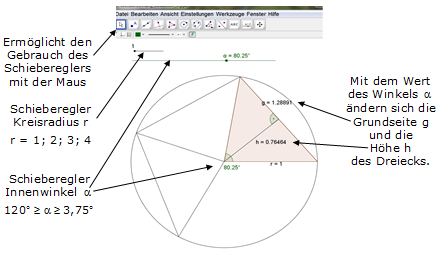
Kreiszahl


Bestimmung der Kreiszahl π – GeoGebra

Lade das Programm Kreisberechnung_Exhaustion_3.ggb. Stelle die Schieberegler auf r = 1 und = 120°. In dem abgebildeten Kreis ist ein gleichschenkliges Dreieck einbeschrieben, das aus drei kongruenten Teildreiecken besteht. Die Grundseite eines Teildreiecks ist g und die Höhe h. Mit Hilfe dieser Angaben kann der Flächeninhalt und der Umfang des gesamten Dreiecks berechnet werden. Siehe hierzu die Zeile für n = 3 in der ersten Tabelle.

Stelle den Radius auf r = 1 ein und verändere den Winkel α. Bei den in der Tabelle genannten Winkelwerten können kongruente Teildreiecke so in den Kreis gezeichnet werden, dass ein regelmäßiges n-Eck entsteht. Notiere in der Tabelle die Werte von g und h auf fünf Nachkommastellen genau.

Berechne dann den Flächeninhalt und den Umfang der n-Ecke. 

r = 1 LE

n

Winkel

h in LE

g in LE

Flächeninhalt in FE

Umfang n·g
in LE

Dreieck

n-Eck

3

120°

0,50000

1,73205

0,43301

1,29904

5,19615

6

60°

         
 

30°

         
 

15°

         
 

7,5°

         
 

3,75°

         

Betrachte die Entwicklung der Werte für den Flächeninhalt und den Umfang. Welche Werte könnten sich für n = 1000 ergeben? Trage sie ein:

   

Stelle den Radius mit dem Schieberegler auf r = 2.

r = 2 LE

n

Winkel

h in LE

g in LE

Flächeninhalt in FE

Umfang in LE
n·g

Dreieck

n-Eck

3

120°

         

6

60°

         
 

30°

         
 

15°

         
 

7,5°

         
 

3,75°

         

Betrachte die Entwicklung der Werte für den Flächeninhalt und den Umfang. Welche Werte könnten sich für n = 1000 ergeben? Trage sie ein:

   

Stelle den Radius mit dem Schieberegler auf r = 3.

r = 3 LE

n

Winkel

h in LE

g in LE

Flächeninhalt in FE

Umfang in LE
n·g

Dreieck

n-Eck

3

120°

         

6

60°

         
 

30°

         
 

15°

         
 

7,5°

         
 

3,75°

         

Betrachte die Entwicklung der Werte für den Flächeninhalt und den Umfang. Welche Werte könnten sich für n = 1000 ergeben? Trage sie ein:

   

Fasse Deine Ergebnisse für große Werte von n, also für n = 1000, zusammen.

Kreiszahl5

Es gibt eine irrationale Zahl, die einen eigenen Namen hat. Es ist die Zahl π (Pi) mit dem Wert  π = 3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 …

Stelle eine Vermutung für die Berechnung des Umfangs und des Flächeninhalts eines Kreises auf:

A =

u =


Bestimmung der Kreiszahl π – GeoGebra – Lösung

r = 1 LE


n 		 

h in LE

g in LE

Flächeninhalt in FE

Umfang n·g
in LE

Dreieck

n-Eck

 

3

120°

0,50000

1,73205

0,43301

1,29904

5,19615

6

60°

0,86603

1,00000

0,43302

2,59808

6,00000

12

30°

0,96593

0,51764

0,25000

3,00001

6,21168

24

15°

0,99144

0,26105

0,12941

3,10580

6,26520

48

7,5°

0,99786

0,13081

0,06527

3,13260

6,27888

96

3,75°

0,99946

0,06544

0,03270

3,13944

6,28224

Betrachte die Entwicklung der Werte für den Flächeninhalt und den Umfang. Welche Werte könnten sich für n = 1000 ergeben? Trage sie ein:

3,14

6,28

r = 2 LE


n 		 

h in LE

g in LE

Flächeninhalt in FE

Umfang n·g
in LE

Dreieck

n-Eck

3

120°

1,0000

3,46410

1,73205

5,19615

10,39230

6

60°

1,73205

2,00000

1,73205

10,39230

12,00000

12

30°

1,93185

1,03528

1,00000

12,00003

12,42336

24

15°

1,98289

0,52210

0,51763

12,42320

12,56040

48

7,5°

1,99572

0,26161

0,26105

12,53041

12,55728

96

3,75°

1,99893

0,13088

0,13081

12,55776

12,56448

Betrachte die Entwicklung der Werte für den Flächeninhalt und den Umfang. Welche Werte könnten sich für n = 1000 ergeben? Trage sie ein:

12,56

12,56

r = 3 LE


n 		 

h in LE

g in LE

Flächeninhalt in FE

Umfang n·g
in LE

Dreieck

n-Eck

3

120°

1,5000

5,19615

3,89711

11,69134

15,58845

6

60°

2,59808

3,00000

3,89712

23,38272

18,00000

12

30°

2,89778

1,55291

2,25000

26,99995

18,63492

24

15°

2,97433

0,78316

1,16469

27,95252

18,79584

48

7,5°

2,99358

0,39242

0,58737

28,19378

18,83616

96

3,75°

2,99839

0,19631

0,29431

28,25347

18,84576

Betrachte die Entwicklung der Werte für den Flächeninhalt und den Umfang. Welche Werte könnten sich für n = 1000 ergeben? Trage sie ein:

28,25

18,86

Ergebnis

Radius r

Durchmesser d

Flächeninhalt A

 

Umfang u

 

1 LE

2 LE

3,14 FE

3,14

6,28 LE

3,14

2 LE

4 LE

12,56 FE

3,14

12,56 LE

3,14

3 LE

6 LE

28,25 FE

3,14

18,86 LE

3,14

Vermutung:

Kreiszahl 6

Ergänzung        
Sind die trigonometrischen Funktionen bekannt (siehe Lehrplaneinheit 12 Trigonometrie), so kann der Flächeninhalt eines regelmäßigen n-Ecks wie folgt berechnet werden. Die Bestimmung des Grenzwertes für  ist jedoch mit den Mitteln der Schulmathematik nicht möglich. 

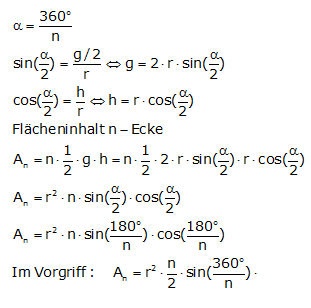
Kreiszahl

 

1   © International GeoGebra Institute, 2013; www.geogebra.org

2   Screenshot © International GeoGebra Institute, 2013; www.geogebra.org ; CC BY NC SA 3.0


100a_kr_bestimmen_kreiszahl_gg_ju: Herunterladen [doc][687 KB]
100a_kr_bestimmen_kreiszahl_gg_ju: Herunterladen [pdf][326 KB]
100a_kr_kreisberechnung_exhaustion_3: Herunterladen [ggb][9 KB]

Weiter zu Fehlersuche: Möndchen des Hippokrates