Forschungsaufträge: Volumen einer Pyramide
Schnelle Gruppen bestimmen noch die Oberfläche „ihrer“ Pyramide.

Foto: C.Uhl
Gruppe A: Plexiglas-Modelle
Vergleiche das Volumen der Pyramide mit dem Volumen des Prismas.

Foto: C.Uhl
Gruppe B: Holz-Modelle
Vergleiche das Volumen der Pyramide mit dem Volumen des Prismas.

Foto: C.Uhl
Gruppe C: Gläserpyramide
Baue aus den Trinkgläsern eine Pyramide auf und vergleiche die Anzahl der benötigten Gläser mit der Anzahl an Gläsern, die du für einen gleich hohen Turm benötigen würdest, der in der untersten Schicht die gleiche Anzahl an Gläsern besitzt.

Foto: C.Uhl
Gruppe D: Mosy
Schneide aus dem Quader eine Pyramide aus, die in Höhe und Grundfläche mit dem Quader übereinstimmt. Welchen Anteil des Quaders hast du abgeschnitten?

Foto: C.Uhl
Gruppe E: Drei Pyramiden
Vergleiche das Volumen der Pyramiden mit dem Volumen des Prismas.
Begründungsaufträge: Volumen einer Pyramide
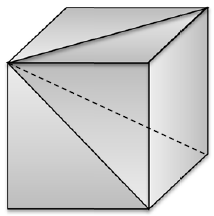
Abb.: C.Uhl
Begründungsauftrag 1:
Begründe, dass die drei Pyramiden, aus denen der Würfel zusammengesetzt ist, in allen Maßen übereinstimmen.
Leite daraus das Volumen einer Pyramide ab und erläutere die Formel
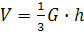
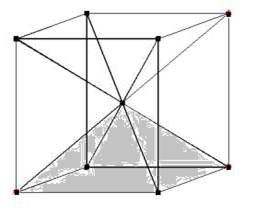
Abb.: C.Uhl
Begründungsauftrag 2:
Begründe, dass die sechs Pyramiden, aus denen der Würfel zusammengesetzt ist, in allen Maßen übereinstimmen.
Leite daraus das Volumen einer Pyramide ab und erläutere die Formel
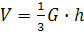
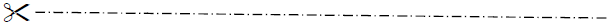
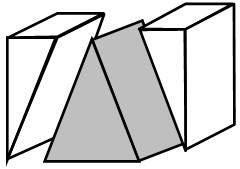
Abb.Schritt 1: C.Uhl
Begründungsauftrag 3:
Begründe, dass im ersten Schritt die Hälfte des Quaders abgeschnitten wurde.
Welchen Volumenanteil hat demnach der Teilkörper I?
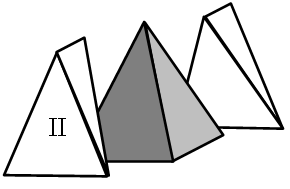
Abb. Schritt 2: C.Uhl
Im zweiten Schritt werden die beiden Teilkörper II so abgeschnitten, dass eine Pyramide entsteht.
Welchen Volumenanteil hat der Teilkörper II?
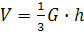
Forschungsaufträge: Volumen einer Pyramide: Herunterladen [pdf][196 KB]
Weiter zu Volumen und Oberfläche der Kugel
