Expertengruppen
Expertengruppe 1
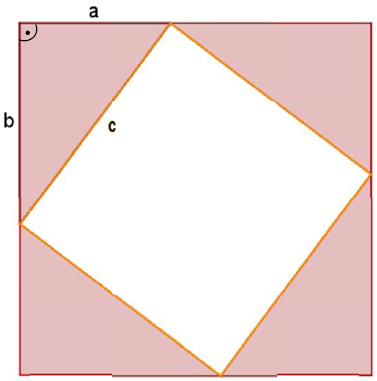
Beweis über Flächenvergleich
Vier kongruente rechtwinklige Dreiecke werden so angeordnet, dass sie ein Quadrat „mit Loch“ bilden.
TIPP:
Für den Flächeninhalt des Quadrats (samt „Loch“) lassen sich zwei unterschiedliche
Terme aufstellen.
Expertengruppe 2
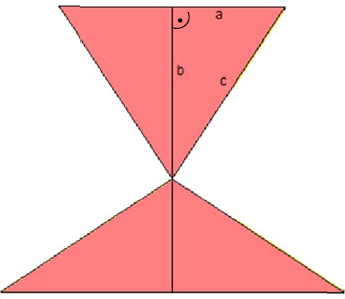
Beweis über Flächenvergleich
Mithilfe der nebenstehenden Figur kann der Beweis zum Satz des Pythagoras geführt
werden.
Die roten Dreiecke sind kongruent und rechtwinklig.
TIPP: Im Verlauf des Beweises wird die Formel für den Flächeninhalt eines Trapezes benötigt:
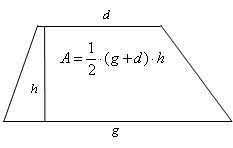
Expertengruppe 3
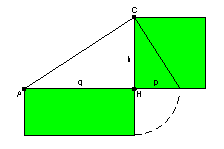
Beweis mit Hilfe des Satzes von Thales
Nutze als Voraussetzung den Höhensatz:
In einem rechtwinkligen Dreieck ist das Quadrat über der Höhe des Dreiecks flächengleich zu dem Rechteck aus den beiden zugehörigen Hypotenusenabschnitten:
.
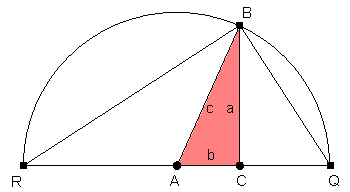
Ein rechtwinkliges Dreieck wird gemäß nebenstehender Abbildung in einen Halbkreis mit Radius c eingepasst.
Expertengruppe 4

Beweis mit Hilfe der Ähnlichkeit
Ein rechtwinkliges Dreieck lässt sich durch seine Höhe in zwei Teildreiecke zerlegen, die zueinander und zum Ausgangsdreieck ähnlich sind.
TIPP:
- Begründet die Ähnlichkeit der Dreiecke ABC, CAH und BCH.
- Durch Aufstellen entsprechender Seitenverhältnisse können die Kathetensätze
beweisen werden.
Kathetensätze:
b2 = c×q
a2 = c×p
Gruppenpuzzle „Pythagoras-Beweise“: Herunterladen [pdf][476 KB]
Weiter zu Beweisinspirationen
