Interaktive Objekte

1. Punkte als "Ansatz"

Definiert man einen Punkt im Koordinatensystem, kann er jederzeit mit dem Mauszeiger versetzt werden. Es lassen sich auch Punkte auf Geraden oder auf Kreisen definieren, welche beim Versetzen nur auf der Geraden oder auf dem Kreis bleiben. Dies funktioniert bei jedem Objekt. Schon bei den einfachen Figuren hat man gesehen, dass sich Objekte verändern, wenn man einen Punkt bewegt.

Beispiel aus der Geometrie

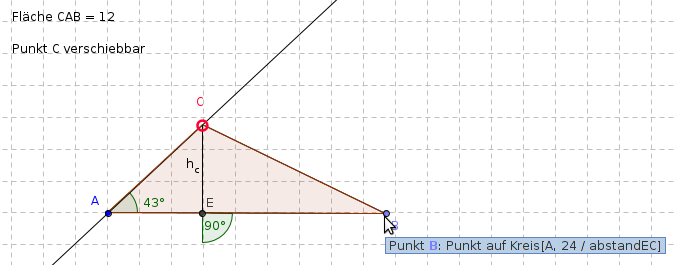
Das in Abbildung 1 gezeigte Beispiel wurde mit GeoGebra erstellt. Es enthält einen interaktiven Punkt C, welchen man auf der angezeigten Geraden verschieben kann.

Abbildung 1: Punkt B ist abhängig von der Position von Punkt C

Beim Verschieben des Punktes C auf der Geraden wird der Abstand des Punktes B vom Punkt A jeweils angepasst. Blau gekennzeichnet ist zu erkennen, wie der Punkt B definiert ist. Er wurde in Abhängigkeit von der Höhe (Abstand des Punktes E vom Punkt C) des Dreiecks festgelegt und das genau so, dass der Flächeninhalt 12 ergibt - daher rührt die 24 in der Berechnung.
Zur genaueren Betrachtung: ggb-Datei [8 kb] bzw. html-Datei [11 kb] .

Beispiel aus der Differenzialrechnung

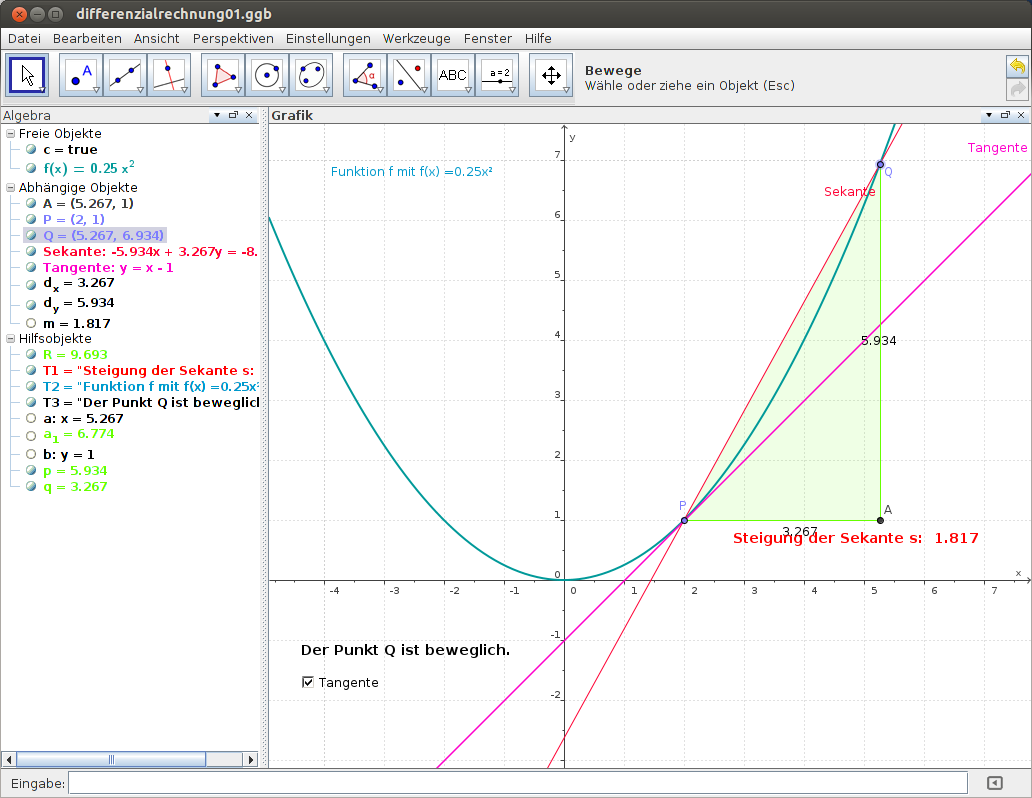
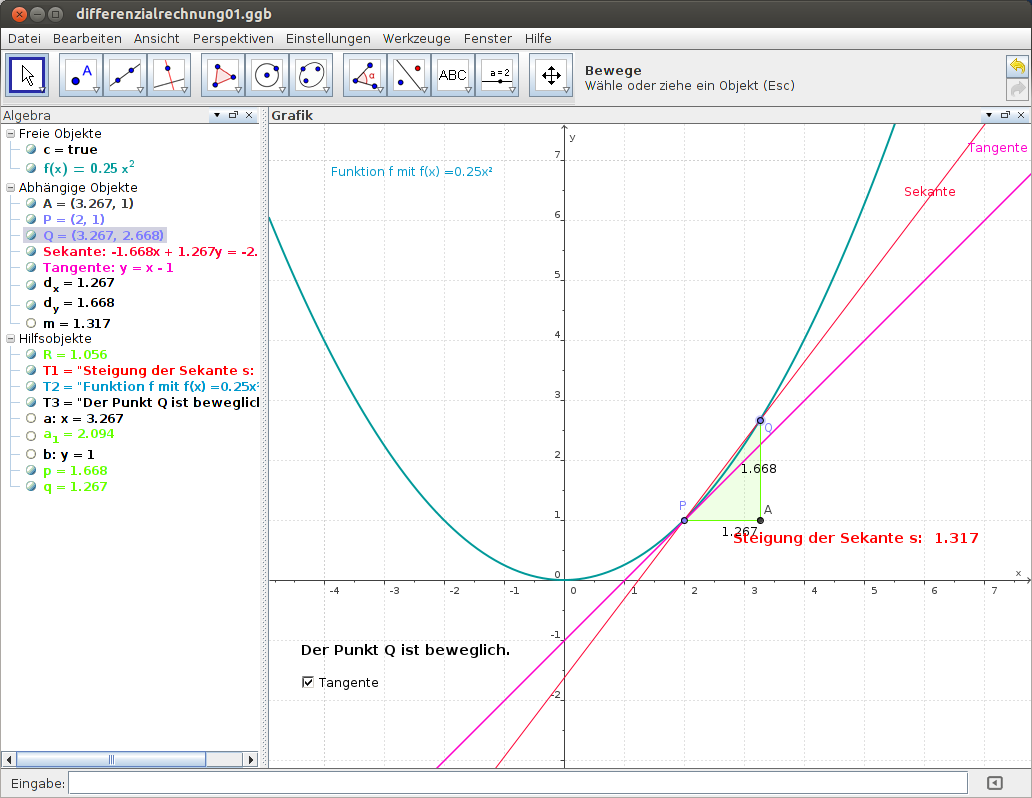
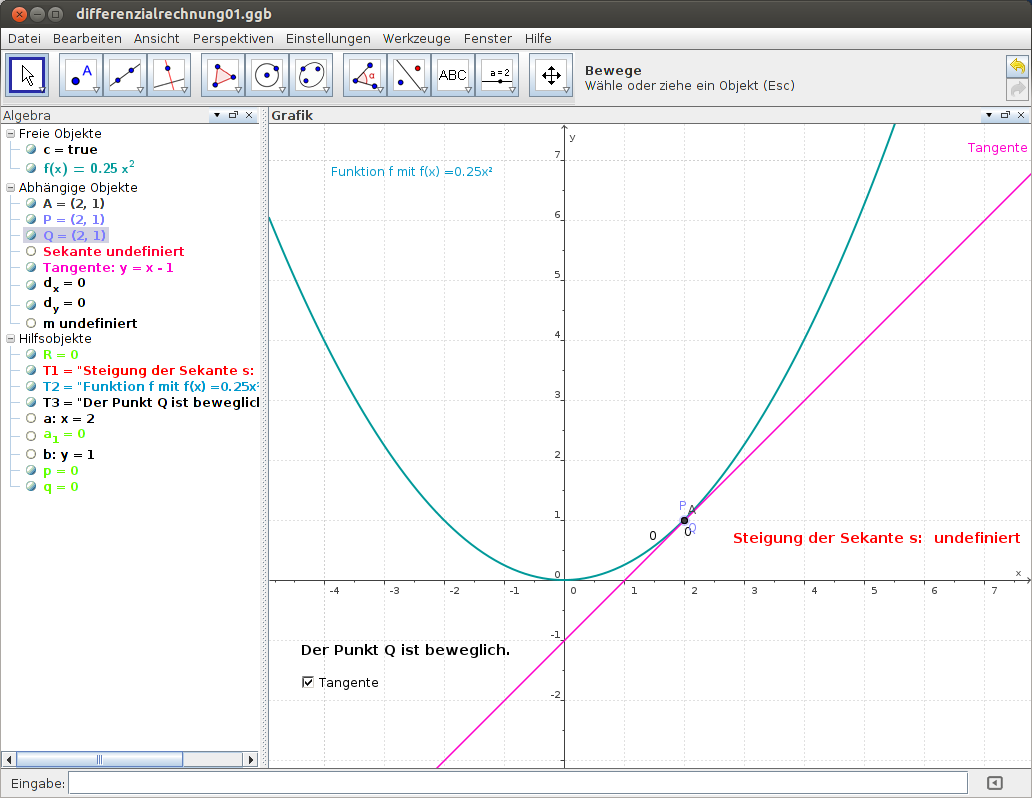
Bei der Einführung der Differenzialrechnung ist es immer wichtig, sich auf bildhafte Weise der Thematik zu nähern. Anhand dieser Grafik erkennt man: je kleiner der Abstand zwischen den Punkten P und Q ist, desto ähnlicher werden die Steigungen der Tangente bzw. Sekante. Fallen P und Q schließlich zusammen, so sind die Steigungen gleich bzw. die Sekante wird zur Tangente (vgl. Abbildung 4).

Abbildung 2: Sekante und Tangente	Abbildung 3: Sekante und Tangente

	ggb-Datei [9 kb] html-Datei [11 kb]
Abbildung 4: Sekante und Tangente fallen zusammen

2. Schieberegler

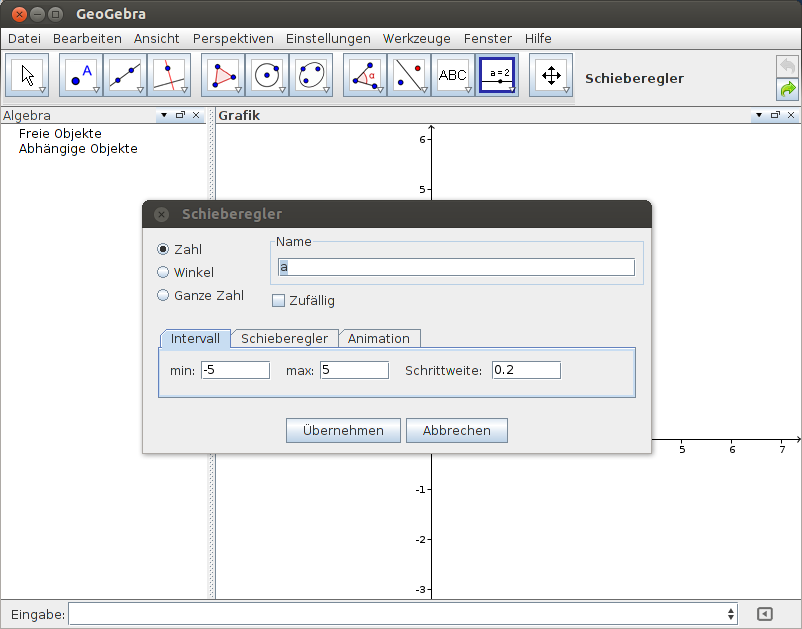
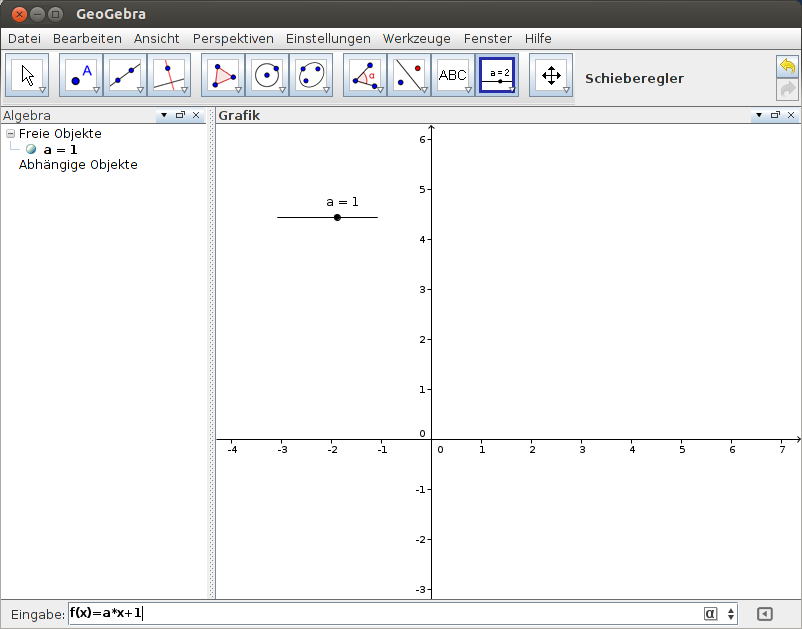
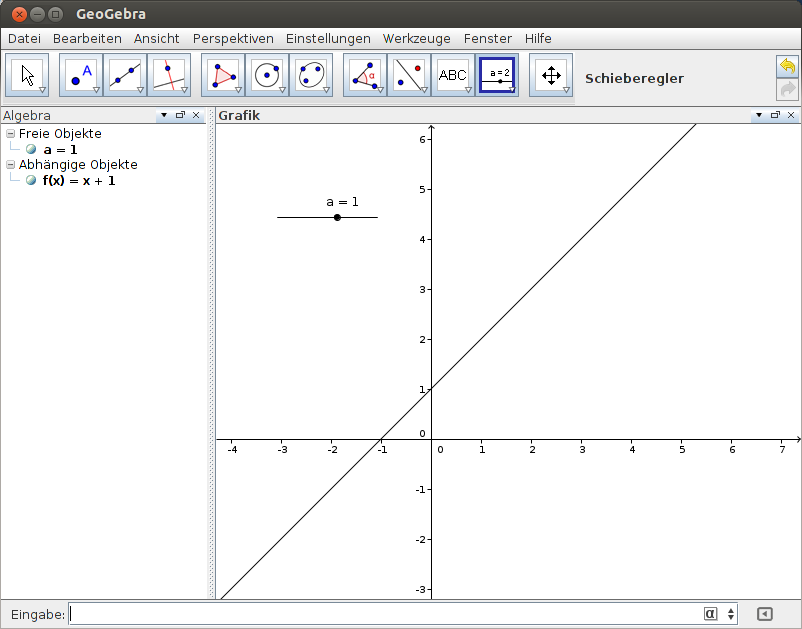
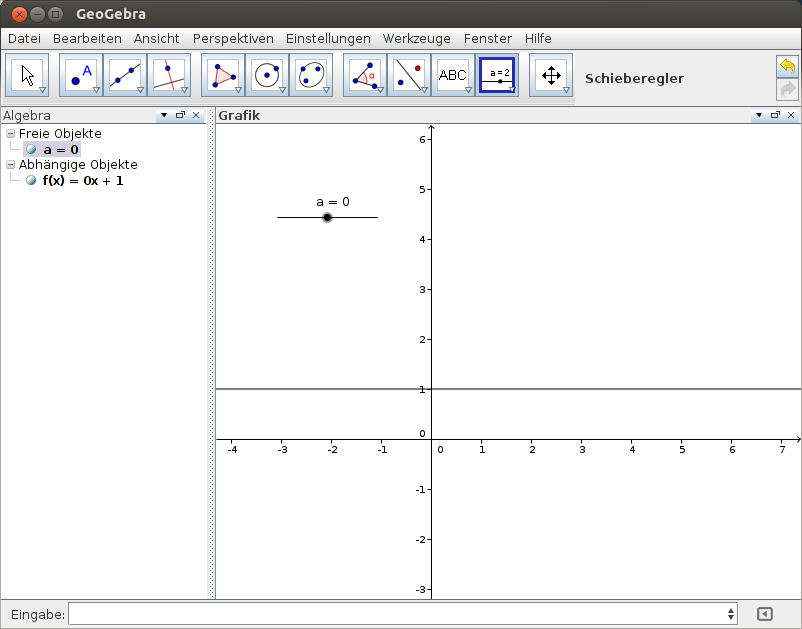
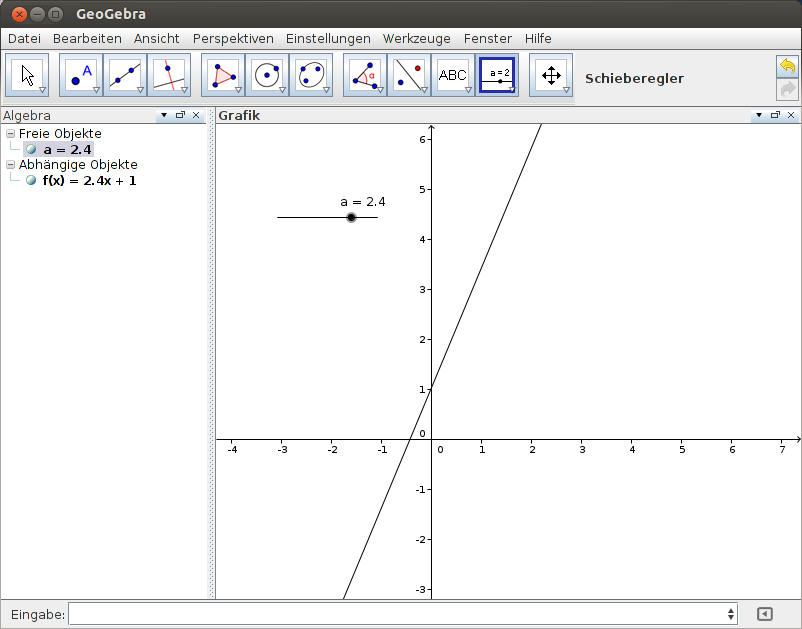
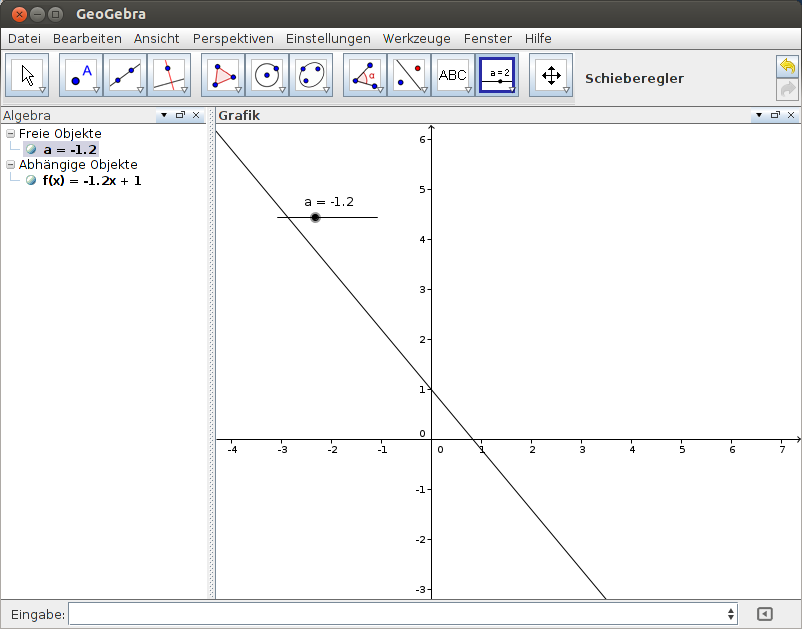
Effektiver, aber etwas anspruchsvoller, sind Schieberegler. In der Werkzeugleiste sind sie ganz rechts untergebracht. Schieberegler sind im Grunde nichts anderes als Variablen, die in einzelnen Formeln verwendet werden können. Im Beispiel in Abbildung 5 heißt der Schieberegler a . Er wird in einem separaten Fenster definiert und kann auch später noch verändert werden. Wird er als Steigung für eine lineare Funktion (vgl. Abbildung 6) verwendet, so führt man ihn einfach als Variable in der Eingabezeile an. Mit dem Schieberegler kann man anschließend verschiedene Variationen der Funktion betrachten (vgl. Abbildungen 7 - 10).

Abbildung 5: Schieberegler definieren	Abbildung 6: Funktion definieren

Abbildung 7: Schieberegler anwenden	Abbildung 8: Schieberegler anwenden

Abbildung 9: Schieberegler anwenden	Abbildung 10: Schieberegler anwenden

Beispiel aus der Integralrechnung

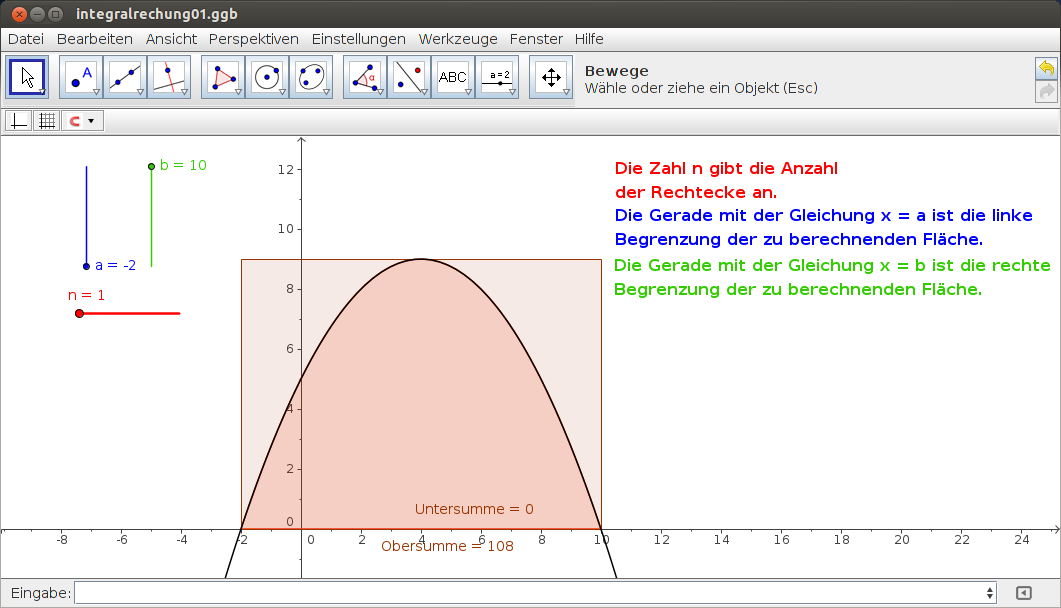
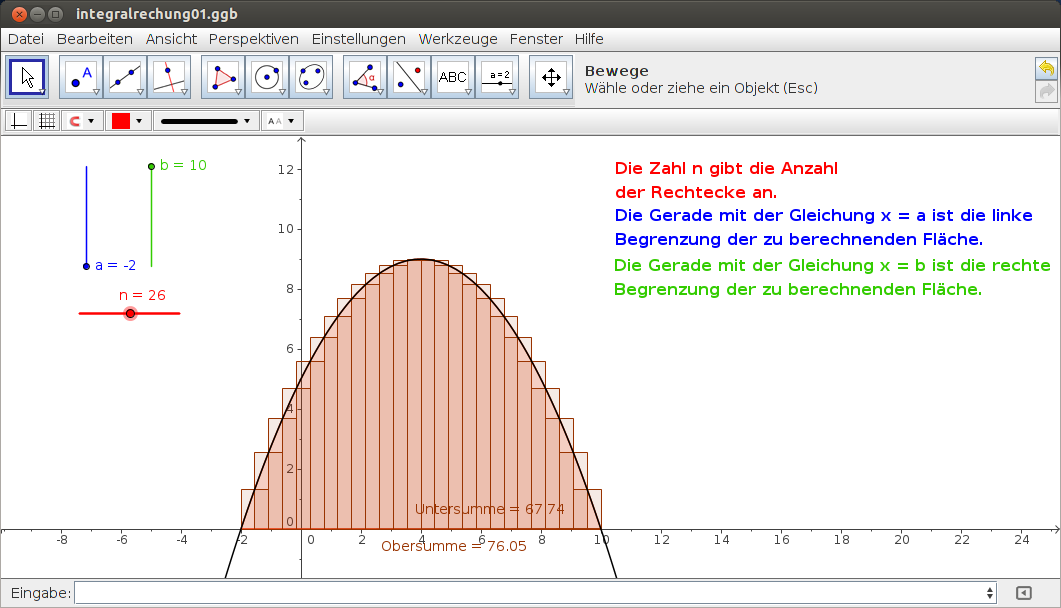
Sehr anschaulich ist auch dieses Beispiel aus der Analysis, bei dem der Flächeninhalt unter einer Kurve mit Rechtecken angenähert wird. Die Schrittweiten lassen sich einstellen, genauso wie die untere und obere Grenze a und b.

Abbildung 11: Fläche durch 1 Rechteck angenähert	Abbildung 12: Intervallverkleinerungen

	ggb-Datei [6 kb] html-Datei [11 kb]
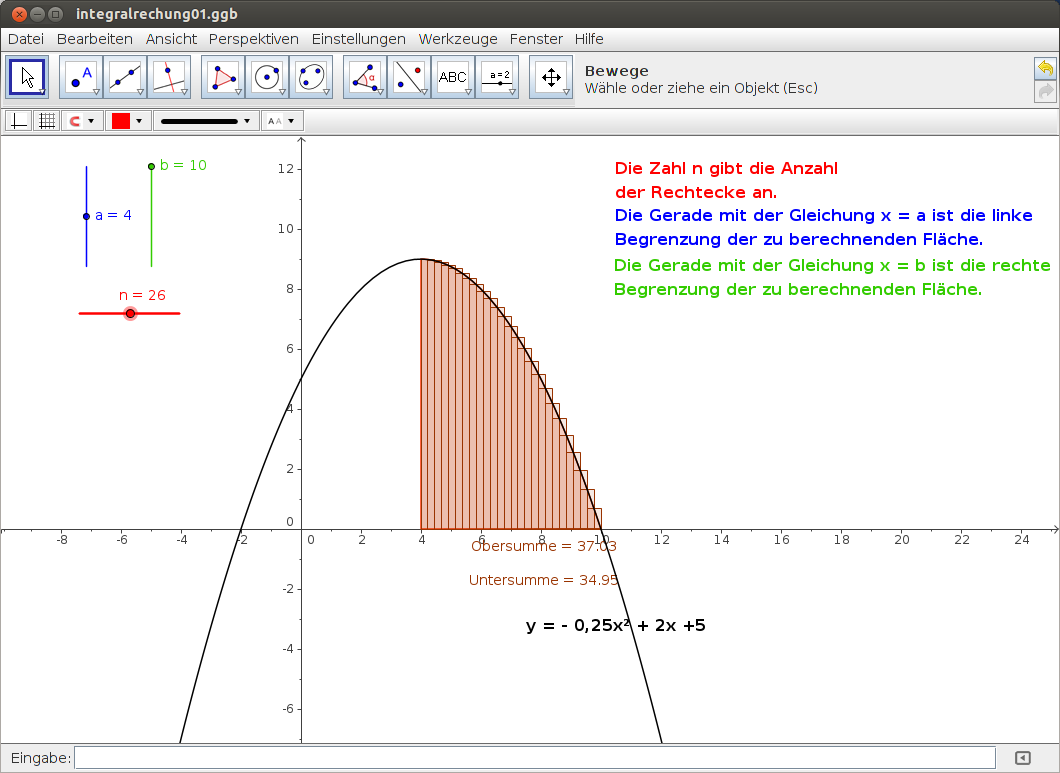
Abbildung 13: untere Grenze wird angepasst

Weiter mit Export von Objekten