Berechnen und Messen

Die in der Schule gebräuchlichen Anwendungen bezüglich geometrischer Berechnungen und Messungen beschränken sich auf Flächeninhalte, Abstände und Winkel.

Bei den unten stehenden Abbildungen kann man durch einen Maus-KLICK auf das Bild jeweils eine größere Darstellung betrachten.

1. Berechnen von Flächeninhalten

Flächeninhalte können nur von Vielecken, Kreisen oder Kegelschnitten berechnet werden. Bei Funktionen können auch Flächen unterhalb eines Funktionsgraphen angezeigt und berechnet werden.
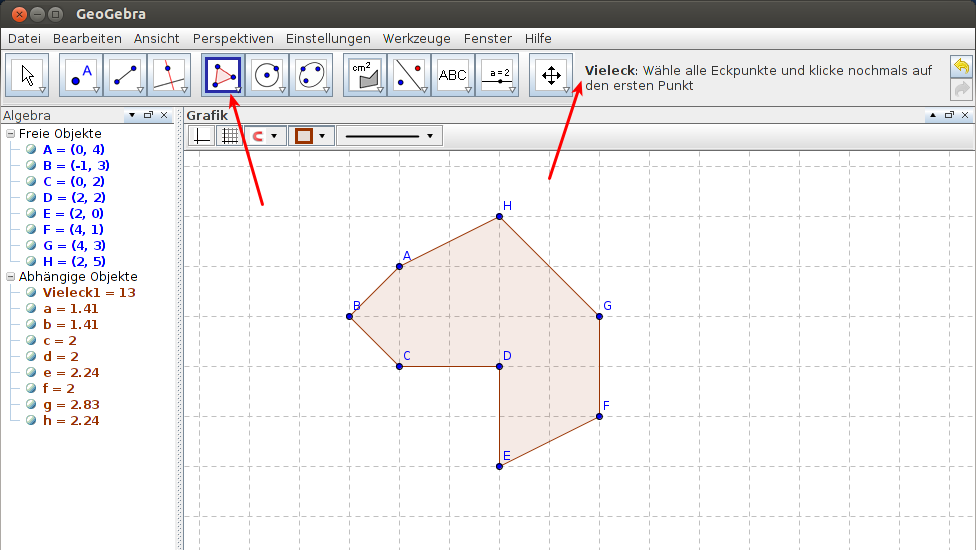
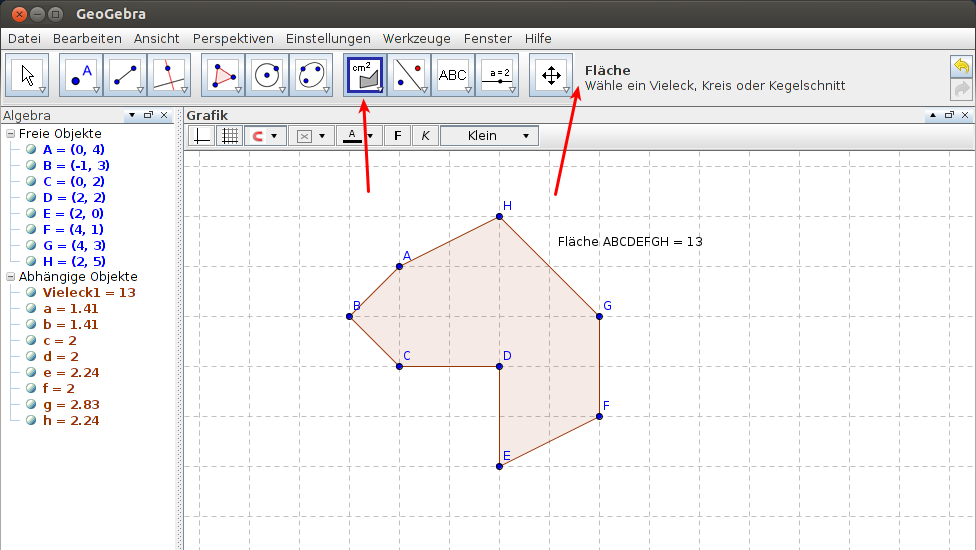
Hier im Beispiel (vgl. Abbildungen 1 + 2) ist ein beliebiges 8-Eck zu sehen, welches mit dem "Vieleck"-Werkzeug gezeichnet wurde. Der Flächeninhalt wird automatisch mit dem entsprechenden Werkzeug berechnet, dabei muss das Objekt nicht erst in kleinere Objekte (Dreiecke, Rechtecke,...) unterteilt werden, sondern wird einfach nur angeklickt. Der angezeigte Flächeninhalt kann beliebig im Grafik-Menü verschoben werden.

Abbildung 1: beliebiges 8-Eck	Abbildung 2: Benutzen des Flächen-Werkzeugs

2. Messen von Abständen

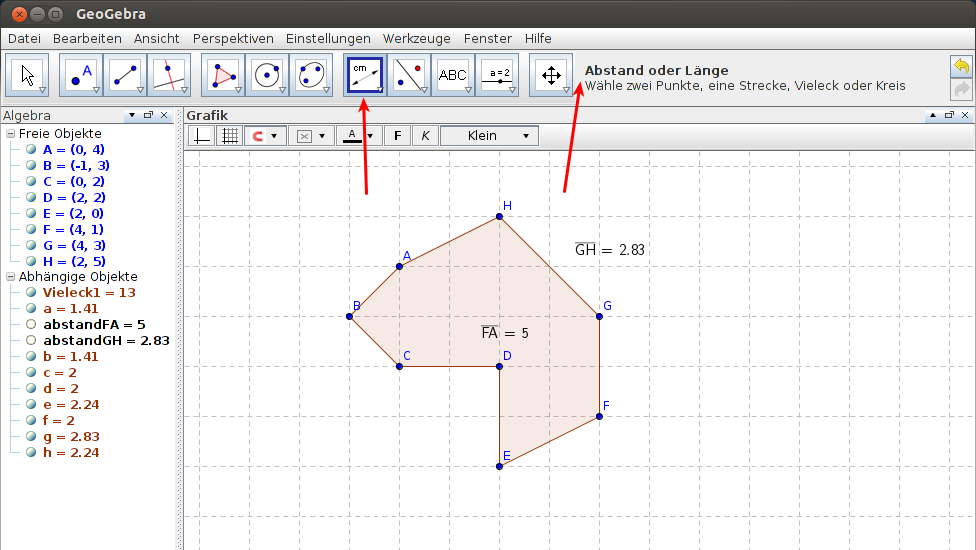
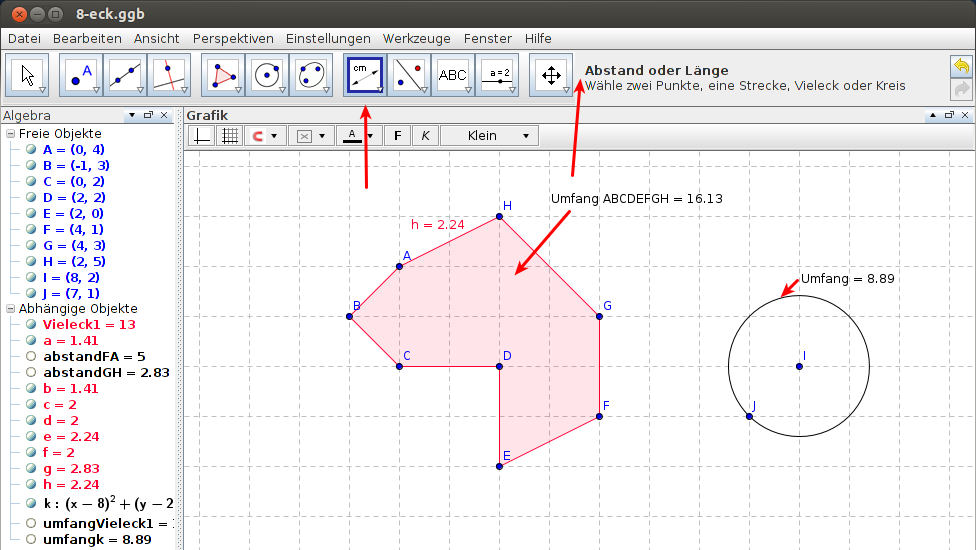
Bei Abständen sind mindestens zwei Punkte oder eine geschlossene Strecke nötig. Im gleichen Beispiel wie zuvor kann der Abstand zwischen zwei beliebigen Punkten gemessen werden, indem man die Punkte nacheinander anklickt. Die Länge einer Strecke misst man mit einem Klick auf dieselbe (vgl. Abbildung 3). Bei Formen oder Figuren kann auch der Umfang bestimmt werden, ohne zuvor alle Einzelstrecken aufsummieren zu müssen. Bei Figuren muss man dabei in die Figur klicken, als würde man den Flächeninhalt bestimmen wollen. Bei Formen, wie beispielsweise einem Kreis, muss man auf die Kreislinie klicken, da innerhalb des Kreises keine Fläche erkannt wird (vgl. Abbildung 4).

Abbildung 3: Abstand zweier Punkte	Abbildung 4: Umfang und Strecken

3. Messen von Winkeln

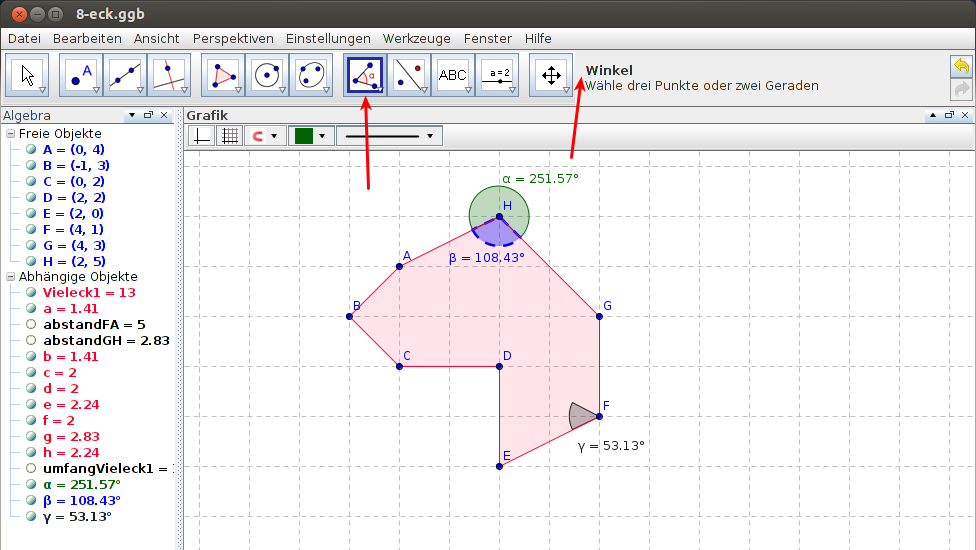
Winkel werden entweder zwischen zwei Strecken oder mittels dreier Punkte bestimmt. Dabei muss darauf geachtet werden, dass man die Strecken (Schenkel) bzw. Punkte entgegen des Uhrzeigersinns auswählt, ansonsten erhält man den entgegengesetzten Winkel. Im Beispiel (vgl. Abbildung 5) ist der Winkel α der Winkel zwischen den Strecken GH und HA (bzw. den Punkten G, H und A), der Winkel β liegt dagegen zwischen den Strecken AH und HG, also genau anders herum. Der Winkel γ liegt zwischen den Punkten D, F und E.

Abbildung 5: Winkel-Werkzeug

Weiter mit Konstruktionen