Konstruktionen

Konstruiert man ein Objekt, so meint man damit, dass einem nur ein Zirkel und ein Lineal zur Verfügung stehen. Das heißt, ein regelmäßiges Dreieck oder Quadrat darf somit nicht mit dem Werkzeug für regelmäßige Vielecke gezeichnet werden. Man geht also genau so vor, als würde man das Objekt von Hand zeichnen bzw. konstruieren. Möchte man bestimmte Maße für Seiten oder Winkel haben, so kommt man um eine derartige Konstruktion sowieso nicht herum. Ist das Dreieck erstmal fertig gestellt, so kann man zu weiteren Konstruktionen auch die Werkzeugkisten benutzen.

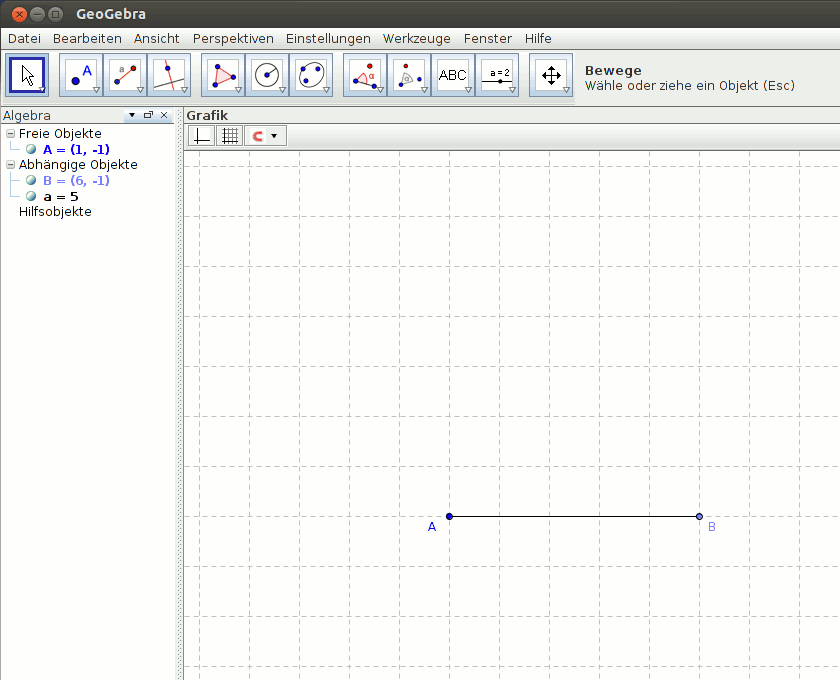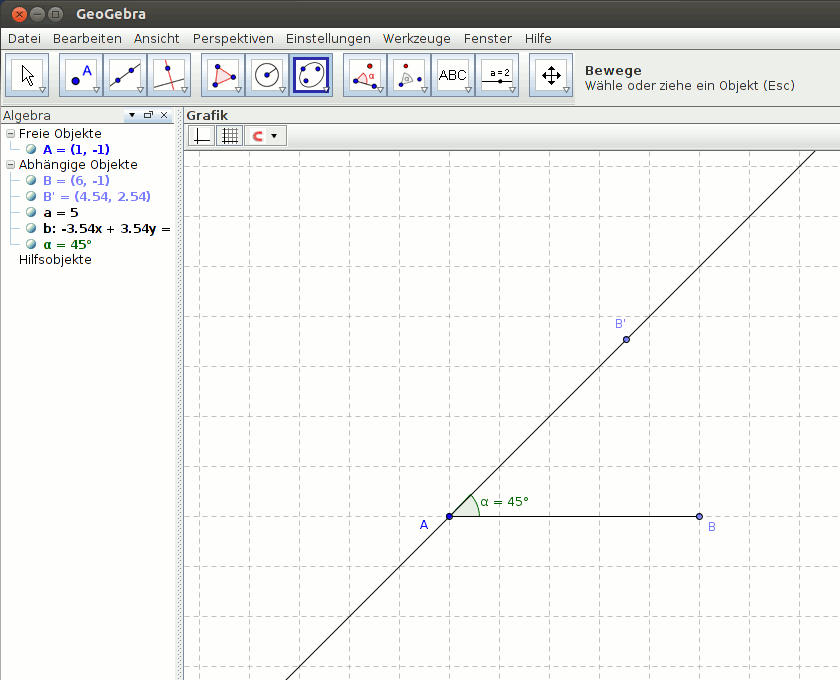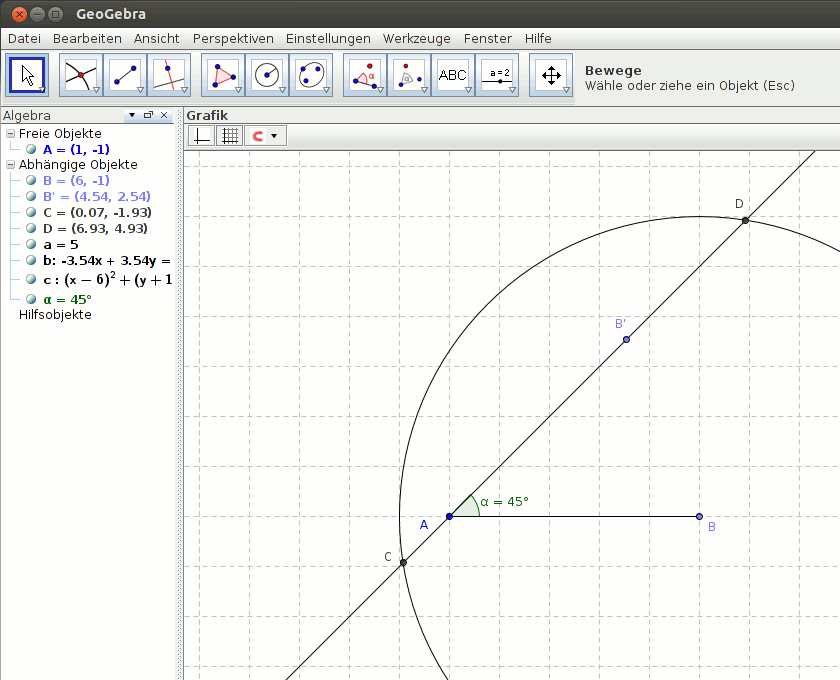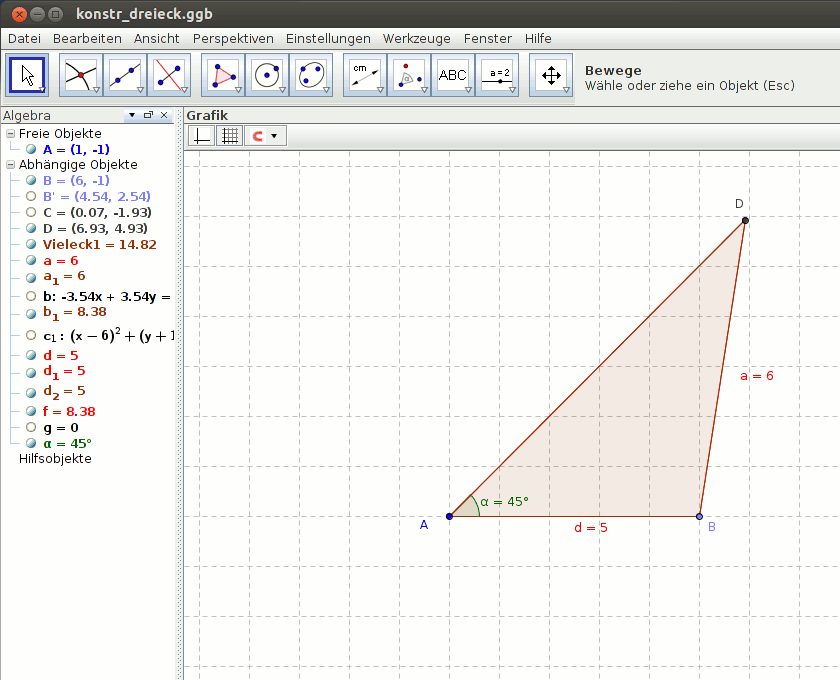
Im folgenden Beispiel wird ein Dreieck mit den Seitenlängen AB = 5cm, α = 45° und BC = 6cm gezeichnet. Anschließend wird der Schwerpunkt (Schnitt der Seitenhalbierenden) und in einem weiteren Schritt der Inkreismittelpunkt (Schnitt der Winkelhalbierenden) des Dreiecks bestimmt.

Abbildung 1: Konstruktion des Dreiecks

Konstruktion des Schwerpunktes:

Ausgangspunkt ist das fertiggestellte Dreieck von Abbildung 1. Die Mitte einer Dreiecksseite bestimmt man mit dem Konstruktionswerkzeug "Mittelsenkrechte" und erhält so die Punkte F und G. Diese verbindet man jeweils mit der gegenüberliegenden Ecke des Dreiecks und erhält so den Schwerpunkt des Dreiecks.

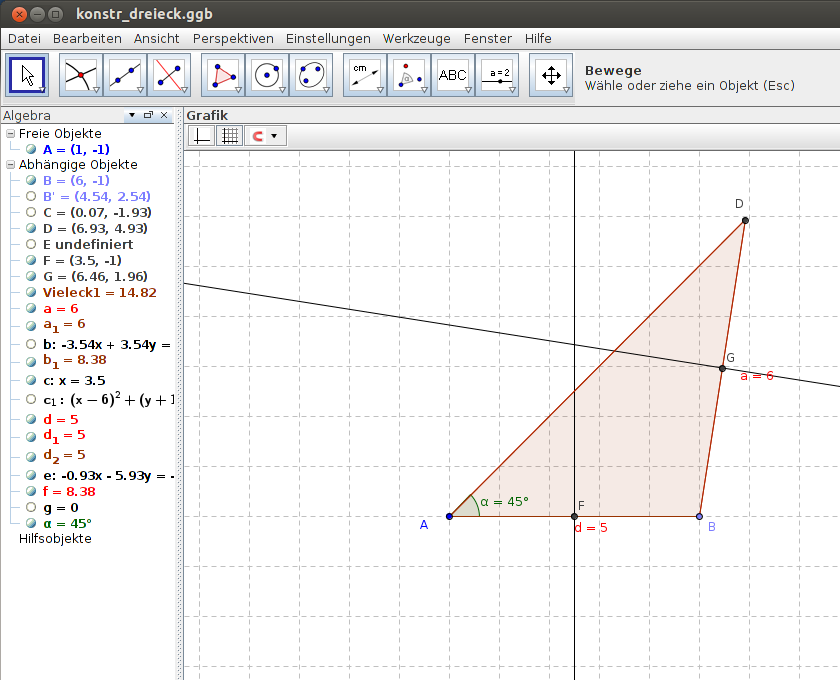
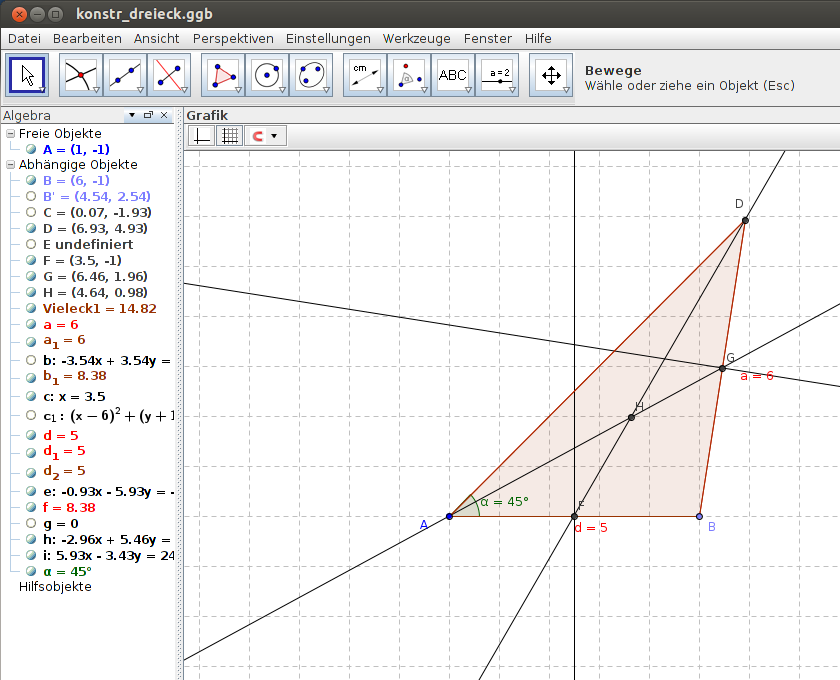
Abbildung 2 + 3: Konstruktion des Schwerpunktes

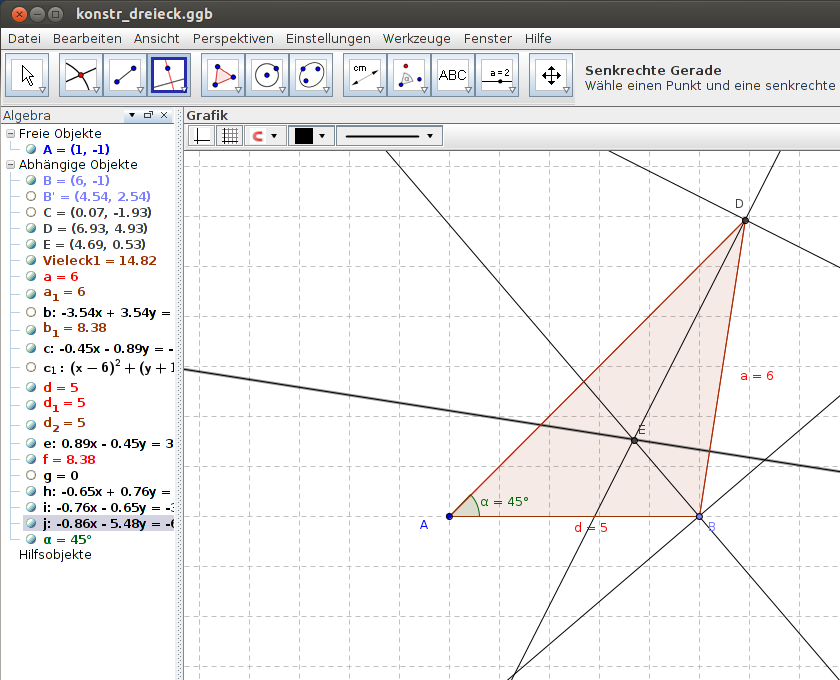
Konstruktion des Inkreismittelpunktes:

Ausgangspunkt ist wiederum das Dreieck von Abbildung 1. Der Inkreismittelpunkt als Schnitt der Winkelhalbierenden erhält man auf ähnliche Weise wie oben den Schwerpunkt. Das Konstruktionswerkzeug hilft uns dabei und wir können uns einige Schritte sparen. Vergessen darf man nur nicht den Punkt F auf der Dreiecksseite, der orthogonal zur Seite durch den Punkt E geht, so dass man den richtigen Radius des Kreises bestimmen kann.

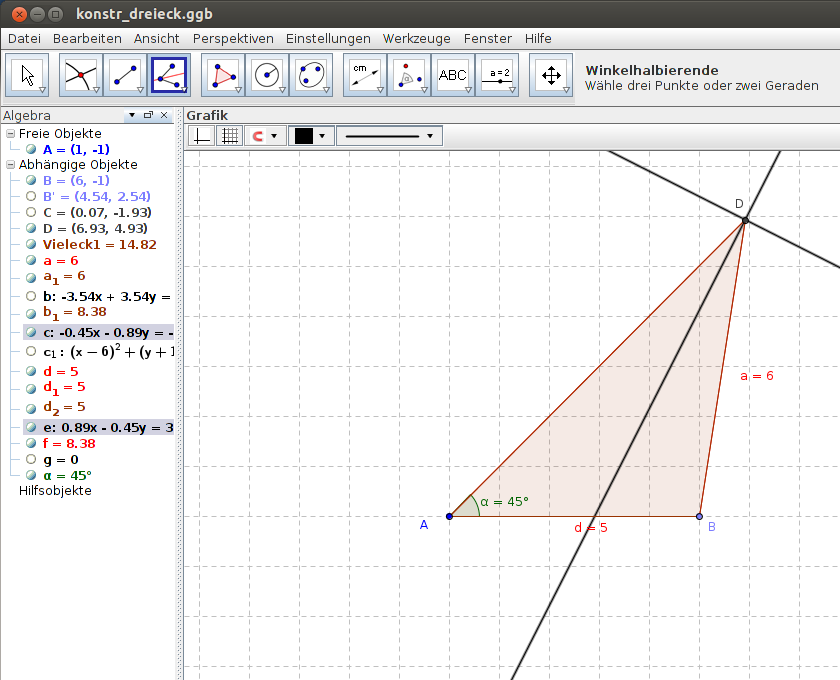
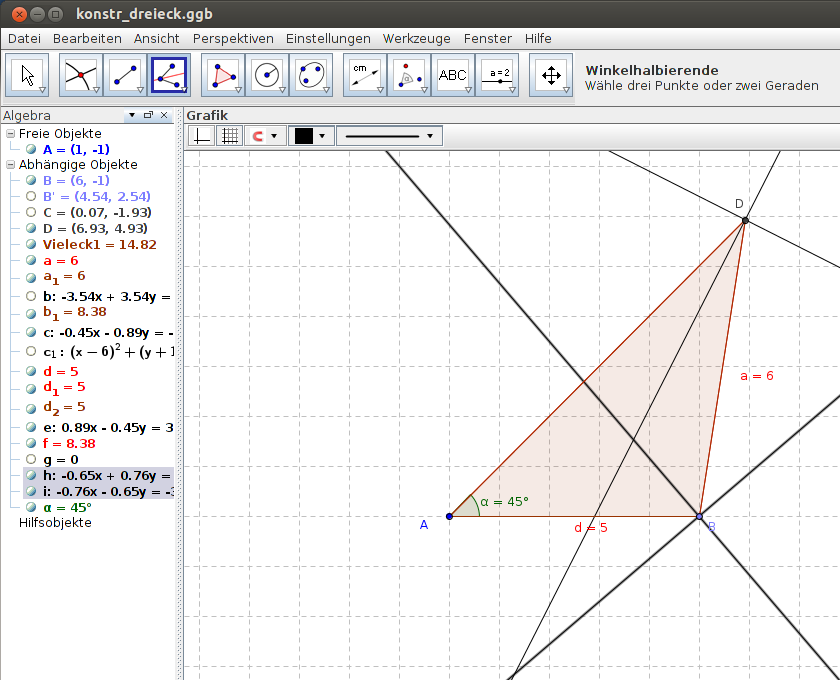
Abbildung 4 + 5: Konstruktion Inkreismittelpunktes

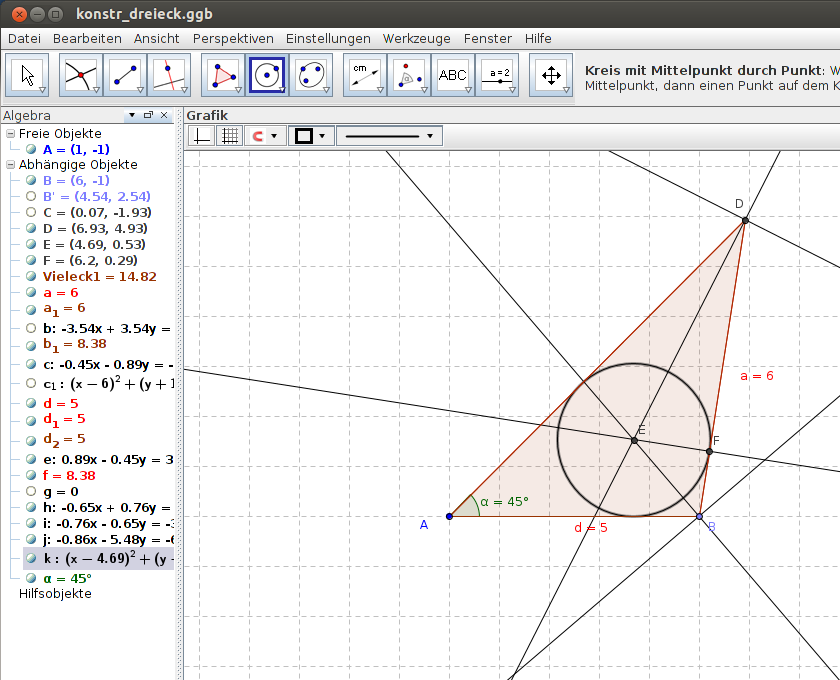
Abbildung 6 + 7: Konstruktion des Inkreises

Weiter mit Funktionen