Repräsentation eines Graphen

Graph als Matrix: Adjazenzmatrizen

In die Adjazenzmatrix (bzw. Nachbarschaftsmatrix) eines Graphen wird an jeder Stelle eingetragen, ob eine Kante zwischen den Knotenpaaren existiert. Bei n Knoten erhält man eine quadratische n x n -Matrix. In Multigraphen trägt man die Anzahl der Kanten zwischen den beiden Knoten in der Matrix ein, bei gewichteten Graphen das Gewicht der Kante. Daher muss bei diesen ein bestimmter Eintrag in der Matrix kennzeichnen, dass gar keine Kante existiert (z.B. „-“).

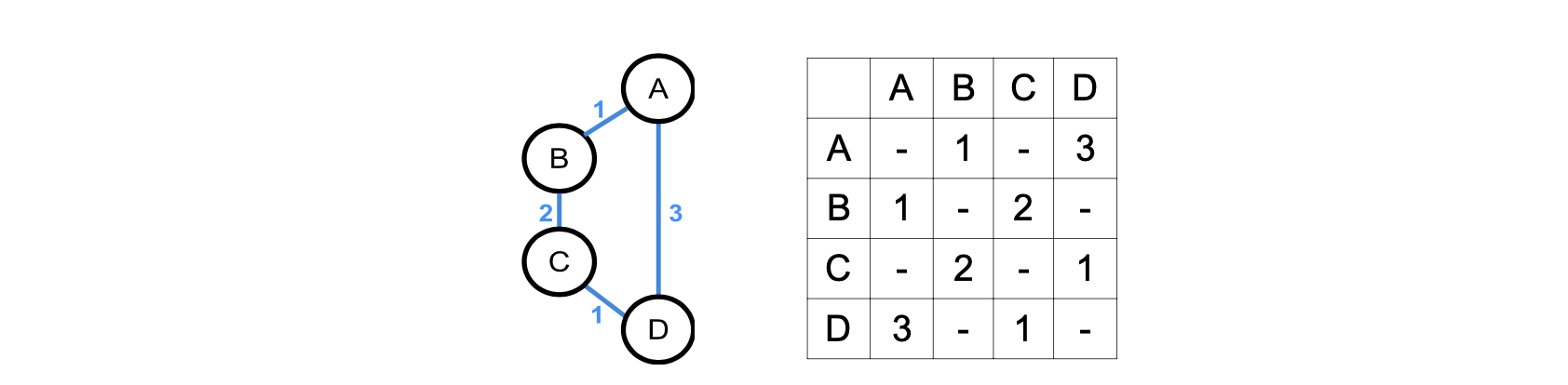
Adjazenzmatrix eines gewichteten Graphen ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt

Bei ungerichteten Graphen ist die Adjazenzmatrix spiegelsymmetrisch zur Diagonalen. Die Diagonale ist in der Regel unbesetzt (es sei denn der Graph hat Schlaufen). Bei gerichteten Graphen wird nur dann eine „1“ eingetragen, wenn der Knoten, der durch die Zeile des Eintrags festgelegt ist, der Startknoten ist und der Knoten, der durch die Spalte festgelegt wird, der Zielknoten ist.

Denkbar wäre auch eine Inzidenzmatrix (Knoten-Kanten-Matrix), bei der eine „1“ steht, wenn ein Knoten auf einer Kante liegt, andernfalls eine „0“. Bei n Knoten und m Kanten ergibt sich so eine n x m – Matrix. Diese Repräsentation eines Graphen wird in der Informatik aber so gut wie nicht verwendet.

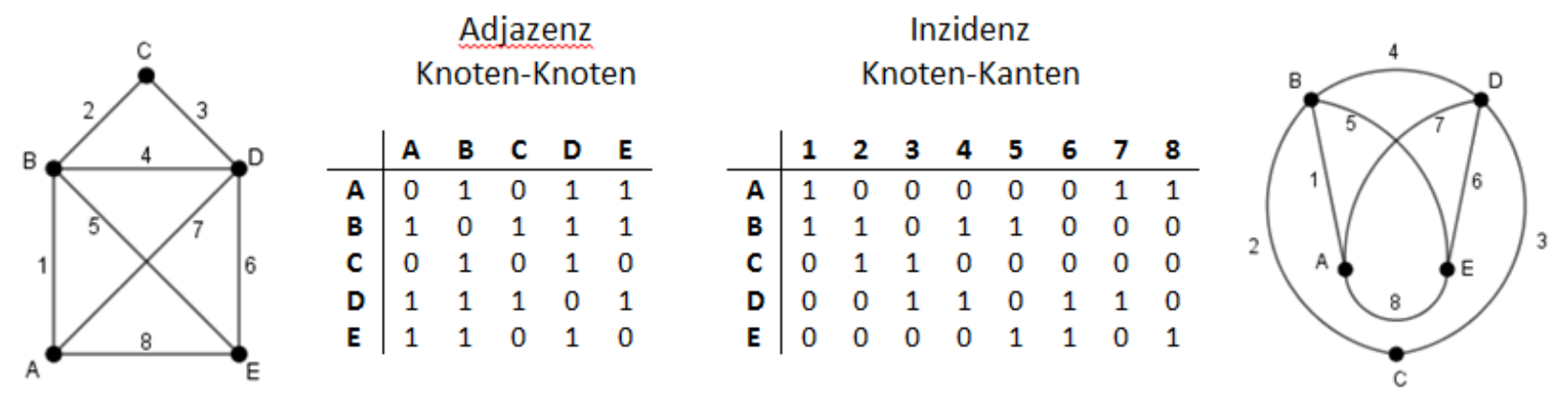
Adjazenz- und Inzidenztabelle zum Haus des Nikolaus und topologisch äquivalenten Graphen (Die Knoten sind mit A-E bezeichnet und die Kanten mit 1-8 durchnummeriert) ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt

Graph als Kantenliste: Adjazenzliste

Bei der Repräsentation des Graphen als Adjazenzliste wird für jeden Knoten eine Liste der benachbarten Knoten gespeichert. Dadurch ist festgelegt, welche Knoten durch Kanten verbunden sind. Bei wenigen Kanten pro Knoten wird die Datenmenge so erheblich geringer.

Bei gerichteten Graphen wird ein Knoten nur dann als Nachbar eingetragen, wenn er der Zielknoten der Kante ist. Bei ungerichteten Graphen wird bei beiden Knoten der jeweils andere Knoten der Kanten als Nachbar eingetragen, da die Kante in beiden Richtungen durchlaufen werden kann.

Bei gewichteten Graphen muss zusätzlich zu jedem Nachbarn noch das Gewicht der Kante dorthin gespeichert werden. Man erhält also ein Tupel.

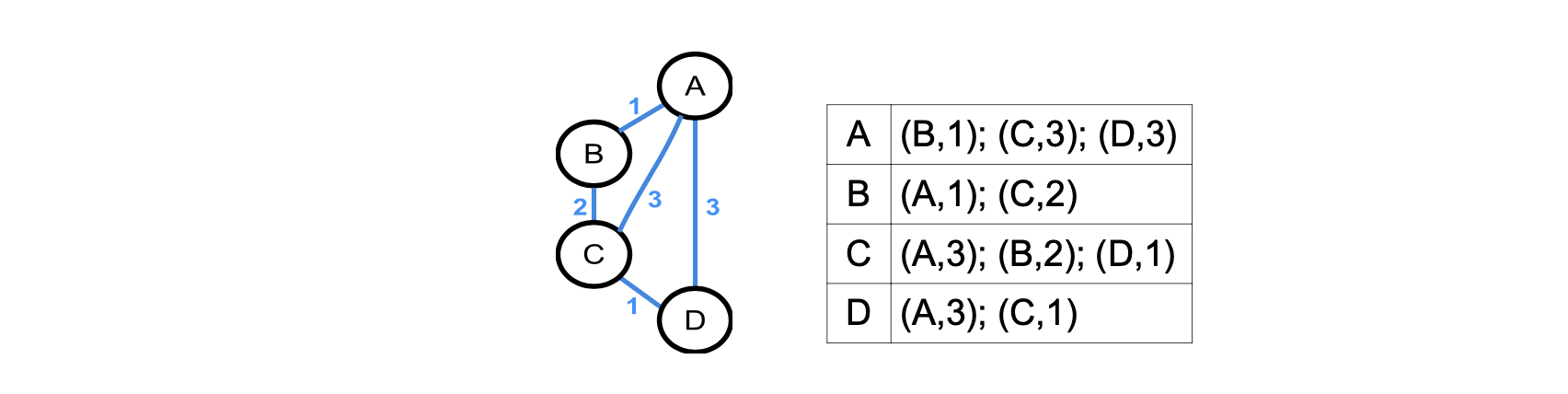
Adjazenzliste eines gewichteten Graphen ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt

Vergleich der Repräsentationsformen

Sowohl in der Form als Adjazenzmatrix, als auch als Adjazenzliste sieht man sehr schön, wenn zwei Graphen isomorph sind. Es wird deutlich, dass es nicht darauf ankommt, an welcher Stelle ein Knoten eingezeichnet wird und wie die Kanten verlaufen.

In der Praxis muss der Knoten aber an einer bestimmten Stelle dargestellt werden. Daher muss ein Programm zur Darstellung und Analyse von Graphen, die Position jedes einzelnen Knoten zusätzlich speichern. Für die Darstellung der Kanten wählt man am einfachsten eine gradlinige Verbindung zwischen den Knoten.

Das im Graphentester verwendete Dateiformat lässt sowohl die Speicherung als Adjazenzliste als auch als Adjazenzmatrix zu. Da es sich um Textdateien handelt, kann man sie mit einem beliebigen Texteditor untersuchen.

Um sich für eine Repräsentationsform zu entscheiden, muss daher der spezielle Anwendungsfall betrachtet werden. Adjazenzlisten erlauben eine schnellere Ausführung des Algorithmus, wenn alle Kanten/Nachbarn eines Knoten untersucht werden müssen, da diese nicht eine komplette Zeile der Matrix durchsuchen müssen, um die Nachbarn zu ermitteln. Adjazenzmatrizen lassen dafür eine schnellere Überprüfung zu, ob eine Kante zu einem bestimmten Knoten existiert, da der Eintrag an einer fest definierten Stelle steht. Bei der Entscheidung muss außerdem berücksichtigt werden, ob es sich eher um dünne Graphen (also mit wenigen Kanten) handelt oder um nahezu vollständige Graphen. Nur bei dünnen Graphen sind die Speicherplatzersparnis und der beschriebene Geschwindigkeitsvorteil der Adjazenzliste von Bedeutung. In der Praxis verwendet man meist Adjazenzlisten.⁸

Mögliche Berücksichtigung im Unterricht

Der Bildungsplan der Kursstufe schreibt vor, sowohl Adjazenzlisten als auch Adjazenzmatrizen zu behandeln. Der Bildungsplan von IMP sieht das nicht vor. Gleichwohl war die ZPG IMP der Meinung, dass es sich um einen wichtigen Aspekt in Hinblick auf die Vernetzung mit der Informatik handelt, und deswegen angesprochen bzw. im Rahmen binnendifferenzierender Phasen eingebracht werden sollte. In der Oberstufen können also Schüler schon Vorkenntnisse mitbringen (vgl. 04_aug_ab_graph_tabelle.odt aus den Kopiervorlagen zu IMP Klasse 8 Mathematik - Aussagenlogik und Graphen).

⁸ Wikipedia, siehe Seite „Graph (Graphentheorie)“, URL: https://de.wikipedia.org/wiki/Graph_(Graphentheorie)#Definitionen (abgerufen: 30.3.2018)

Hintergrundinformationen: Herunterladen [odt][990 KB]

Weiter zu Modellierung von Problemen mit Graphen