Froschperspektive vs. Adlerperspektive
Nachdem die Ausgangssituation als Graph modelliert wurde, muss nun der Algorithmus erarbeitet werden. Menschen erfassen den Graphen als Gesamtheit ("Adlerperspektive"), beim Programmieren kann man aber immer nur einen einzigen Knoten bearbeiten. Über bereitgestellte Methoden des Graphen kann man auch auf angrenzende Kanten oder verbundene Knoten zugreifen.
Unplugged
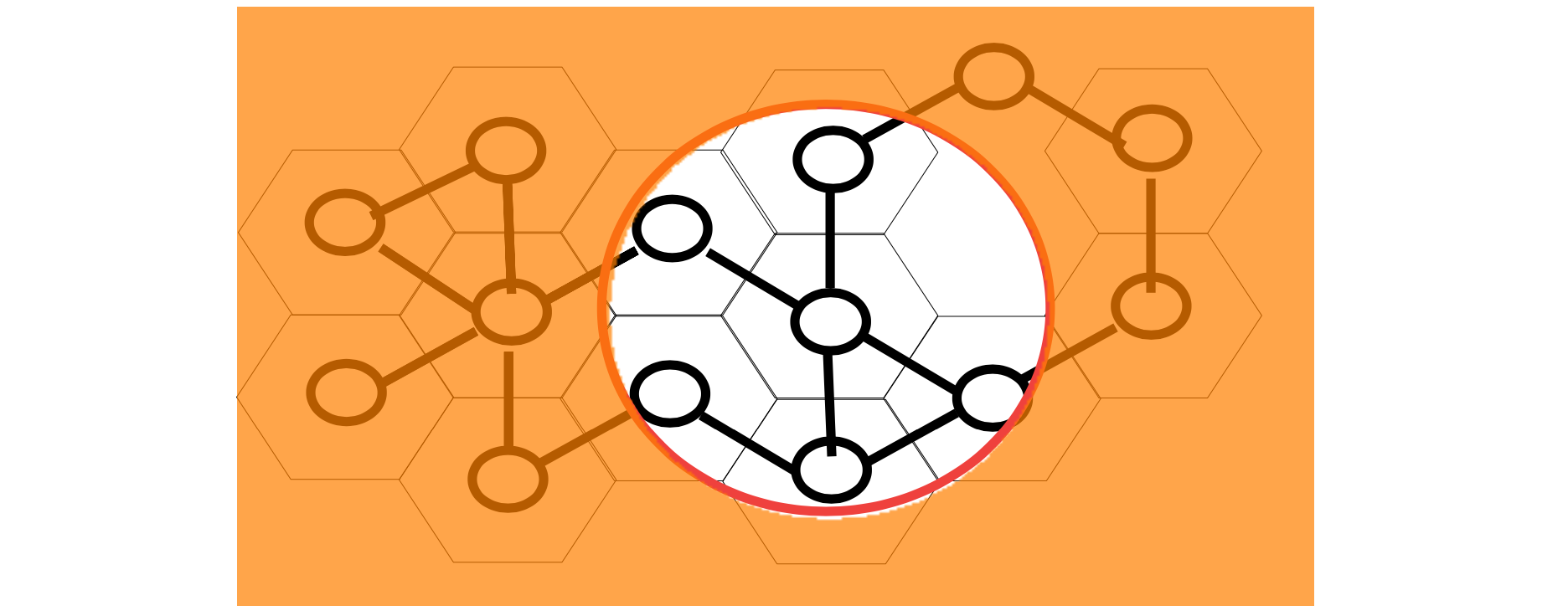
Bildquelle: Graphen von ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 2_unterrichtsverlauf.odt
Daher ist es wichtig, dass die Schüler den Graphen in "Froschperspektive" betrachten, d.h. immer nur einen kleinen Ausschnitt des Graphen im Blick haben. Diese Froschperspektive kann man bei planaren Graphen mit nicht zu vielen Kanten unplugged erreichen, indem man die Knoten hexagonal anordnet. Jeder Knoten kann dadurch Kanten zu höchstens sechs Nachbarn haben. Darüber legt man ein vorgefertigtes Maskenblatt mit Loch, das den Blick nur auf einen einzigen Knoten mit seinen Nachbarn freigibt. Eventuell sollte der Graph mit darüber liegender Schablone von einem anderen Schüler oder der Lehrkraft vorbereitet werden, damit offensichtliche Eigenschaften nicht sofort erfasst werden (z. B. ob der Graph zusammenhängend ist). Auch eine Anordnung auf einem quadratischen Gitter (bis zu 4 bzw. 8 Nachbarn) wäre möglich. Je nach Algorithmus ist es sinnvoll, die Knoten durchzunummerieren, um eine Liste mit noch zu bearbeitenden Knoten führen zu können.
Sollen die noch zu bearbeitenden Knoten in einer Schlange gespeichert werden (Breitensuche), dann kann man die Liste der zu bearbeitenden Knoten einfach hintereinander schreiben und die bearbeiteten Knoten abstreichen:

Bildquelle: Breitensuche von ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 2_unterrichtsverlauf.odt, bearbeitet

Bildquelle: Tiefensuche von ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 2_unterrichtsverlauf.odt, bearbeitet
Der Startknoten war hier K2. Bei der Auswertung dieses Knotens wurden die Knoten K1 und K3 hinzugefügt. K3 ist der nächste zu bearbeitende Knoten, dieser wird vom Stapel entfernt und bei der Bearbeitung K6 und K7 hinzugefügt. Die Bearbeitung von K7 fügt keine weiteren Knoten hinzu. Daher ist K6 der nächste Knoten. Dabei wird K4 und K8 hinzugefügt. K8 ist der aktuell zu bearbeitende Knoten.
Vorteile: In der Maske bekommt man „unplugged“ den didaktisch wünschenswerten Tunnelblick, d.h. man sieht nur die nächste Nachbarschaft des fokussierten Knotens; das Medium zwingt wie ein Schreibtischtest zum Mitdenken, und die händische („enaktive“) Ausführung ist für manche Schüler einfacher zu erlernen als die Bedienung des Graphentesters.
Nachteile: Generell sind nur planare Graphen mit entsprechend regelmäßiger Anordnung möglich. Manchmal sind auch nicht verbundene Knoten mit im Blick (z.B. bei Fokus auf Knoten links unten). Nach der Bearbeitung eines Knotens muss ein neuer Knoten fokussiert werden. Für die Auswahl dieses Knotens ist ein Blick auf den gesamten Graphen notwendig. Die Verwaltung eines Stapels ist recht aufwändig.
Froschperspektive im Graphentester
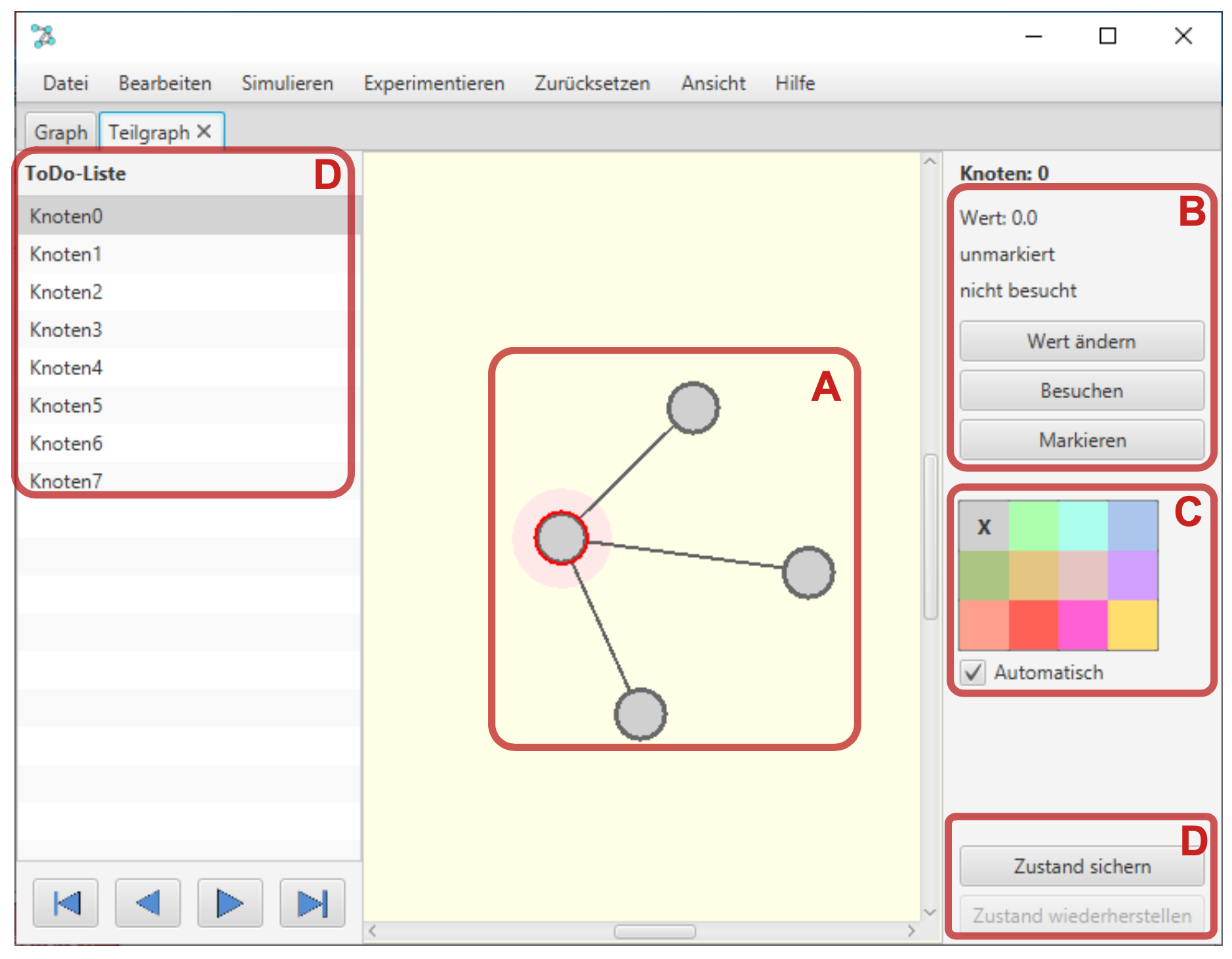
Bildquelle: Graphentester von ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 2_unterrichtsverlauf.odt
Der Graphentester unterstützt das Erproben eines Algorithmus in der Froschperspektive im "Experimentiermodus". Dargestellt werden dabei immer ein Knoten bzw. eine Kante und die dazugehörigen Nachbarn (A). Wird das Hintergrundbild ausgeblendet (Standardeinstellung), dann erkennt man nicht mehr, an welcher Stelle im Graphen man sich befindet.
Die dargestellten Knoten und Kanten können mit der Maus ausgewählt werden und entweder über die Eigenschaften auf der rechten Seite oder mit einem Kontextmenü bearbeitet werden. Dabei ist es nicht möglich, die Struktur des Graphen zu verändern.
Knoten können als "besucht" und als "markiert" gekennzeichnet werden, Kanten als "markiert" und als "gelöscht" (B). Die Farbe eines Knotens ergibt sich entweder automatisch aus diesen Einstellungen (Option "automatisch") oder kann über eine Farbauswahl bestimmt werden.
Darüber hinaus kann der Wert eines Knotens geändert werden (C).
Eine "ToDo-Liste" (D) enthält die noch zu bearbeitenden Knoten / Kanten. Über das Kontextmenü (rechte Maustaste) können Knoten / Kanten der ToDo-Liste hinzugefügt oder aus ihr gelöscht werden. Dadurch dass das Einfügen am Anfang oder am Ende der Liste erfolgen kann, kann die ToDo-Liste als Stapel oder als Schlange verwendet werden und damit Tiefen- oder Breitensuche realisiert werden. Ist über die Ansicht "Knotenwerte anzeigen" ausgewählt, ist es außerdem möglich, die ToDo-Liste zu sortieren und damit eine Prioritätswarteschlange zu realisieren (z.B. für Dijkstra- oder Kruskal-Algorithmus).
Mit der Option "Gehe zu ..." des Kontextmenüs kann man dieses Element in einem neuen Tab öffnen, aber später wieder zum vorherigen Knoten zurückkehren. Damit ist es möglich, einen rekursiven Aufruf durchzuführen. Zusammen mit der Option "Zustand sichern" (D), die den aktuellen Zustand des Graphen sichert und eine Wiederherstellung zu einem späteren Zeitpunkt ermöglicht, kann ein Backtracking-Algorithmus realisiert werden.
Durch diese Möglichkeit kann der Aufrufstack eines rekursiven Algorithmus schön veranschaulicht werden, allerdings ist es deutlich schwerer, den Überblick bei der Durchführung eines Algorithmus zu behalten.
Vorteil: Die Froschperspektive wird zu keinem Zeitpunkt verlassen. Erst am Ende kehrt man zur Gesamtansicht des Graphen zurück und sieht das Ergebnis. Die dabei durchgeführten Aktionen lassen sich sehr leicht auch in einen Algorithmus übersetzen. Die Verwendung einer ToDo-Liste ist eine praktikable Umsetzung vieler Algorithmen.
Nachteil: Das Erlernen der Benutzung des Tools darf nicht der Unterrichtsinhalt sein. Die konsequente Beschränkung auf die Froschperspektive erschwert den Überblick und könnte dadurch manchen Schülerinnen oder Schülern den Zugang zum Algorithmus erschweren.
Unterrichtsverlauf: Herunterladen [odt][298 KB]
Weiter zu Erarbeitung des Algorithmus
