Repräsentation von Graphen

Begriffe: Adjazenzmatrix, Adjazenzliste

In IMP Klasse 8 werden im Themenbereich "Aussagenlogik und Graphen" (Mathematik) die Graphen eingeführt. Schon da wird die Adjazenzmatrix als Repräsentationsform für Graphen verwendet. Auch im Alltag kommen sowohl die Adjazenzliste (z.B. Liste der Freunde von Personen als Grundlage eines Soziogramms) als auch die Adjazenzmatrix (z.B. Entfernungstabellen der großen Städte) vor, ohne dass dort der zugrundeliegende Graph den meisten Menschen bewusst ist.

Die Schülerinnen und Schüler haben bisher gelernt, Problemstellungen in Graphen zu übersetzen. Im Arbeitsblatt "06_repraesentation.odt" werden ausgehend von Alltagsbeispielen die dazugehörigen Graphen erstellt und die Begriffe "gerichtet/ungerichtet" und "gewichtet/ungewichtet" wiederholt. (Aufgaben 1 und 2).

Danach sollte der Lehrer die Begriffe "Adjazenzmatrix" und "Adjazenzliste" formal einführen (Folie 1 der Präsentation 06_repraesentation_laufzeit.odp). Durch Überführung der einen Repräsentation in die andere wird deutlich, dass beide gleichwertig sind (Aufgaben 3 bis 6). Damit hat man die Anforderungen des Bildungsplans erfüllt.

Ergänzung 1: Laufzeitanalyse

Man kann sich aber auch noch die Frage stellen, welche Repräsentation nun die "bessere" ist. Damit stellt sich natürlich die Frage, was man damit machen will. Da bei den dominierenden Mengen die Laufzeit eine große Rolle gespielt hat, kann man sich Gedanken machen, welche Laufzeiten die Grundoperationen auf Graphen in den verschiedenen Repräsentationen haben (weitere Folien der Präsentation 06_repraesentation_laufzeit.odp). Voraussetzung dafür ist, dass die Schülerinnen und Schüler mit Laufzeitanalysen von Listenoperationen auf Array und verketteter Liste vertraut sind. In der Präsentation wird ein Array mit verketteten Listen kombiniert. Es wäre auch möglich, statt des Arrays eine weitere verkettete Liste zu benutzen. Dies würde die Laufzeiten ändern. Diese Details sollten hier aber keine Rolle spielen.

Entscheidend ist aber, ob mit der Anzahl der Knoten automatisch auch die Anzahl der Kanten eines Knoten wächst. In vielen Fällen hängt die Anzahl der Kanten eines Knotens nicht von der Gesamtanzahl der Knoten ab (z.B. gehen von einer Kreuzung in der Regel nur 4 Straßen aus, ein Mensch hat 30-40 nähere Bekannte, auch wenn die Weltbevölkerung steigt usw.). Das andere Extrem ist der vollständige Graph, bei dem jeder Knoten mit jedem anderen verbunden ist (z.B. bei Traveling Salesman Problem).

Wichtig ist es zu erkennen, dass je nach benötigten Operationen, die Repräsentationsform passend gewählt werden sollte. In der Praxis werden Graphen meistens als Adjazenzlisten implementiert, da diese weniger Speicherplatz benötigen. Mathematiker nutzen aber gerne auch Adjazenzmatrizen, da sich manche Algorithmen dann auch als Matrizenmultiplikationen beschreiben lassen⁸ .

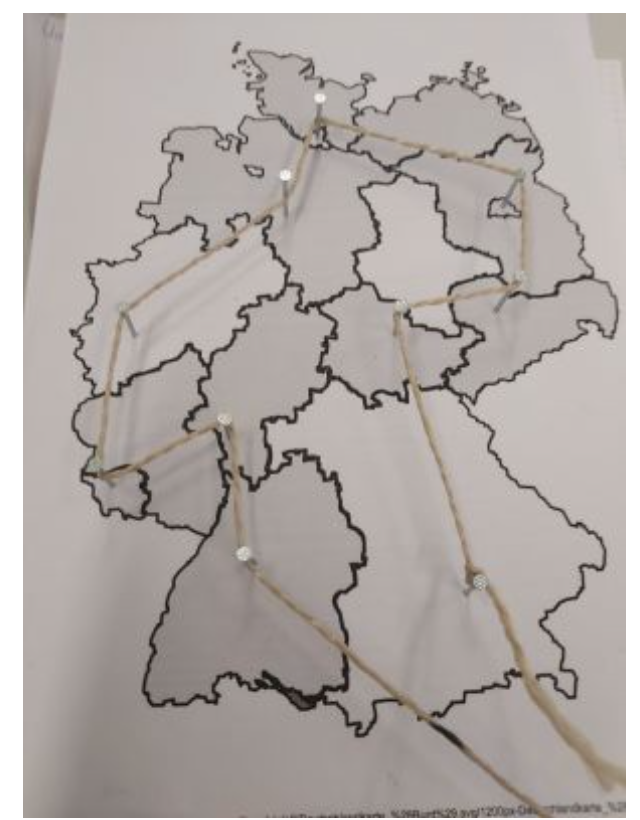
Bildquelle: Enaktive Übung (Holzbrett mit Nägeln und Schnur) ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 2_unterrichtsverlauf.odt

Ergänzung 2: Traveling Salesman Problem

Die Schülerinnen und Schüler können anhand des für die Adjazenzmatrix eingeführten Traveling Salesman Problems das Konzept des Näherungsalgorithmus wiederholen. Hier führt die Überlegung, wie viele mögliche Wege es geben kann, zu n! = n * (n-1) ...* 3* 2 * 1, da das die Anzahl der Möglichkeiten ist n Städte anzuordnen. Auch O(n!) ist für große n eine unpraktikable Laufzeit. Eine schöne Möglichkeit, dies enaktiv zu erfahren, hat man bei einem Holzbrett mit herausstehenden Nägeln (für die einzelnen Städte) und einer Schnur, die um alle Nägel herumgeführt werden muss. Je länger das Reststück der Schnur nach der Rundreise ist, desto kürzer ist die gefundene Rundstrecke. Das Optimum kann man an der Schnur farblich markieren.

Eine Greedy-Näherungslösung erhält man, wenn man in jedem Schritt die nächstgelegen noch nicht besuchte Stadt anfährt. Auch hierfür steht im Graphentester ein Algorithmus bereit, der an einer Deutschlandkarte mit 40 Städten ausprobiert werden kann. Da dies ein relativ einfacher Algorithmus ist, eignet er sich für eine Vertiefung der Implementation von Graphen-Algorithmen. Die Schülerinnen und Schüler hätten dann einen optimalen und einen Näherungsalgorithmus implementiert.

Als Ausblick könnte man im Graphentester andere Ansätze zeigen, um eine Näherungslösung zu finden. Gegebenenfalls könnte dies auch im Rahmen einer GFS von einem Schüler vorgestellt werden.

 

⁸ Z.B. Erreichbarkeit von Knoten (=transitive Hülle), https://me-lrt.de/12-erreichbarkeitsproblem-graph-transitive-hulle (abgerufen 27.10.2020)

 

Unterrichtsverlauf: Herunterladen [odt][298 KB]

 

Weiter zu Kartenfärbeproblem (optional)