Sprachtypen und zugehörige Grammatiken (BP: 2, 6, 9-14)

Auf Seite 3 wurde schon eine Übersicht über verschiedene Typen von Sprachen und Automaten gegeben. Beim Studium der Automaten stand bisher die Erkennung (insbesondere die maschinelle Erkennung) einer Sprache im Mittelpunkt, also die automatische Lösung ihrer Wortprobleme: Gehört eine gegebene Zeichenfolge zu einer gegebenen Sprache?

Grammatiken und reguläre Ausdrücke hingegen dienen der Beschreibung von Sprachen: Damit legen wir fest, aus welchen Wörtern eine Sprache besteht. Diese Beschreibungsmittel sind mit den entsprechenden Automatentypen so eng verbunden, dass aus einer Grammatik (die eine Sprache beschreibt) ein passender Automat (der sie erkennt) sogar automatisch erzeugt werden kann. Im Unterricht empfiehlt es sich, Beschreibung und Erkennung fachsprachlich deutlich zu trennen, weil das den Schülern eine gedankliche Vorsortierung der vielen Konzepte ermöglicht.

Wie für DEAs gibt es auch für Grammatiken eine formale Darstellung, die die Schüler angeben können müssen. Als Beispiel soll hier die Sprache der arithmetischen Ausdrücke dienen, die also Wörter wie „6“ oder „4+1“ oder „(5+2)*7-((5+2)*3)“ enthält; auf Seite 10 wurde schon besprochen, dass diese Sprache wegen der geschachtelten Klammern nicht regulär ist.

Tabelle 2 zeigt die Bestandteile einer Grammatik am Beispiel dieser Sprache:

Tabelle 2: Bestandteile einer Grammatik, Beispielgrammatik für arithmetische Ausdrücke

Begriff	Erläuterung	formal	Beispiel für Rechenausdrücke, Bemerkungen
Menge der Terminale (synonym zu Alphabet)	Menge der Zeichen, die in der Eingabe zulässig sind	Menge ∑	∑ = {+, -,*,/, (, ), 0, 1 \}
Menge der Variablen (auch „Nichtterminale“)	Menge von Platzhaltern, die nach und nach durch Terminale ersetzt werden müssen	Menge V	V = {A, S} Variablen werden üblicherweise mit Großbuchstaben bezeichnet, hier für „Ausdruck“ und „Summand“
Produktionen	Ersetzungsvorschriften, die es erlauben, Variablen durch andere Variablen sowie Terminale zu ersetzen	P ⊂ V x (V ∪ ∑) * siehe Fußnote ²¹	Menge der Produktionen: P= { (1) A → S + S, (2) A → S – S, (3) S → ( A ), (4) S → A, (5) S → 0, (6) S → 1, … und weitere Ziffern }
Startsymbol	Variable, mit der die Ersetzung startet	Startsymbol in V	Startsymbol: A

Jede Produktion ist als Ersetzungsregel zu lesen. Die Produktion A→S+S bedeutet beispielsweise „die Variable A darf durch S+S ersetzt werden“. In den meisten Grammatiken dürfen Variablen und Terminale auf der rechten Seite der Produktion bunt gemischt stehen; im Beispiel ist S wieder eine Variable, das + jedoch ein Terminal der Grammatik. Manche Ersetzungen erzeugen also neue Variablen, die dann weiter ersetzt werden müssen. Die Ersetzung muss immer mit dem Startsymbol der Grammatik beginnen. Sobald keine Variablen mehr vorkommen, sondern nur noch Terminale dastehen und ein Wort bilden, sagt man „das Wort wurde aus der Grammatik hergeleitet“. Die Herleitung besteht dabei aus der Folge von Ersetzungen.

Mit der obigen Grammatik kann man etwa das Wort „1+(0-(1+1))“ aus dem Startsymbol A in 9 Schritten herleiten. Den ersten Schritt liest man als „A wird mit Hilfe von Produktion (1) durch S+S ersetzt“:

	(1)		(6)		(3)		(2)
A	→	S+S	→	1+S	→	1+(A)	→	1+(S-S)

	(5)		(3)		(1)		(6)
	→	1+(0-S)	→	1+(0-(A))	→	1+(0-(S+S))	→	1+(0-(1+S))

	(6)
	→	1+(0-(1+1))

Da sich mit einer Grammatik manche Wörter herleiten lassen und andere nicht, legt auch jede Grammatik eine Sprache fest (eben die Wörter, die sich damit herleiten lassen). Sobald für ein Wort eine solche Herleitung existiert, weiß man also, dass das Wort der Grammatik genügt. Dabei kann es durchaus mehrere Herleitungen für das gleiche Wort geben: Oben könnte vor Produktion 5 auch zunächst Produktion 3 zum Zuge kommen und den zweiten Summanden ersetzen. Die Herleitung von Wörtern mit Hilfe einer Grammatik ist eine Standardaufgabe im schriftlichen Abitur.

Ebenso müssen Schülerinnen für geeignete Grammatiken begründen können, warum sich bestimmte Wörter damit nicht ableiten lassen. So kann man das Wort (((1+1) hier nicht herleiten: Da Klammern nur in Produktion 3 und immer paarweise entstehen, können unpaarige Klammern mit dieser Grammatik also nicht hergeleitet werden. Anders gesagt: Das Wort gehorcht der Grammatik nicht und gehört nicht zur beschriebenen Sprache.

Wie immer empfiehlt es sich, zwischen Beschreibung und Erkennung von Sprachen zu unterscheiden; Grammatiken sind zunächst ein Beschreibungswerkzeug. Für die Einordnung des Unterrichtsstoffs in einen größeren Zusammenhang kann man noch aufzeigen, dass für die Erkennung der beschriebenen Sprache ein Automat so gezielt gesteuert werden müsste, dass er die Herleitung selbständig durchführt.

Nun ist die oben angegebene Grammatik zwar einfach zu verstehen. Sie unterstützt die automatische Herleitung aber nicht, weil sie einen Überblick über die gesamte Eingabe verlangt: Man muss schon zu Beginn das ganze Wort kennen, auf das die Herleitung letztlich zielt, und die Produktionen von Anfang an in einer „geschickten“ Reihenfolge anwenden, beispielsweise für die Zuordnung von Klammern oder die korrekte Berücksichtigung von „Punkt vor Strich“. Kann ein Automat dagegen die Eingabe nur „ein Zeichen nach dem anderen“ anschauen, muss er aus einer anderen Grammatik erzeugt werden (die aber die gleiche Sprache beschreibt).²²

Reguläre Grammatiken, reguläre Sprachen (BP: Item 10)

Man kann die erlaubte Gestalt der Produktionen einschränken. Lässt man beispielsweise nur Produktionen zu, die nach folgenden besonders einfachen Mustern aufgebaut sind…:

N → xA (rechts ein Terminal, dann ein Nichtterminal) oder
S → y (rechts nur ein Terminal) oder
T → ε (leere Produktion, meist mit ε für „empty“ geschrieben)
… dann heißt die resultierende Grammatik eine reguläre Grammatik. Die Sprachen, die man mit regulären Grammatiken beschreiben kann, sind wieder die schon erwähnten regulären Sprachen. Und reguläre Sprachen sind genau die Sprachen, die von DEAs erkannt werden können. Das bedeutet: Zu jeder regulären Grammatik gibt es einen DEAs, der genau die Wörter erkennt, die man mit der Grammatik herleiten kann, und umgekehrt. Reguläre Sprachen lassen sich also mit DEAs verarbeiten und erkennen.

Die Umwandlung zwischen einem DEA und einer zu ihm äquivalenten regulären Grammatik ist nicht schwer: Man erstellt zu jeder Variable einen Zustand und zu jeder Produktion einen Übergang. Die Produktion N→xA bedeutet ja „wenn du ein N erwartest, verbrauche ein x und erwarte dann ein A“, entspricht also einem Übergang von Zustand N mit Eingabezeichen x nach Zustand A. Die ε-Produktionen entsprechen Endzuständen.

Reguläre Ausdrücke (BP: Item 10)

Besonders praktisch ist eine andere Methode, reguläre Sprachen zu beschreiben: Die sogenannten regulären Ausdrücke, die man mit Hilfe regulärer Operatoren formuliert. Die wichtigsten regulären Operatoren sind...

x Erwähnung eines Alphabetzeichens: Hier muss genau ein „x“ stehen.

R* „R-stern“: der reguläre Ausdruck R darf mehrfach (auch 0 mal) hintereinander stehen

RS Verkettung: erst muss etwas stehen, das zum regulären Ausdruck R passt; dann etwas, das zu S passt

R|S Oder: entweder ein R, oder ein S

Mit dieser „Minimalausstattung“ von drei Operatoren lassen sich im Prinzip schon alle regulären Ausdrücke schreiben. Bequemer, kürzer und übersichtlicher geht es, wenn man weitere Operatoren hinzunimmt. Es gibt unterschiedliche „Dialekte“ solcher Erweiterungen; in LibreOffice sind unter anderem die folgenden verfügbar:

R+ „R plus“: mindestens ein mal R (Abkürzung für RR*)

[a-f] Abkürzung für a|b|c|d|e|f

. „Punkt“: genau ein beliebiges Zeichen

R? R optional (darf hier stehen, muss aber nicht)

\. Nach Backslash werden reguläre Operatoren als „normale“ Zeichen angesehen

() Mit Klammern kann man Teilausdrücke gruppieren

Beispiele:

Regulärer Ausdruck	Wortbeispiele	Beschreibung
M(a\|e)(i\|y)er	Maier, Mayer, ...	alle vier Schreibweisen von Meier, Mayer usw.
(0\|1)+	0, 1, 00, 11, 10, 1001000, 000111	beliebig lange, nichtleere Folgen von 0 und 1
0\|(1(0\|1)*)	0, 1, 111, 1010, 10000	Binärzahlen ohne „überflüssige“ führende Nullen (einzelne 0 aber erlaubt)
b+@(b+\.)+\.bb+	b@b.bb bbb@b.b.b.bbbb bb@bbb.b.bbb.bb	„Mailadressen“, die nur b enthalten und deren Topleveldomain mindestens zwei Buchstaben hat
[1-9]+[0-9]*[13579]	17, 84841, 509, 8765	ungerade, mindestens zweistellige Dezimalzahlen
Sch..e	Schule, Schale, Schade, Schrie, Schere, Sch7=e, Schöne, Schote

Die Handhabung von regulären Ausdrücken verlangt etwas Übung, ist aber in vielen Situationen ein äußerst praktisches Hilfsmittel. Auch LibreOffice erlaubt die Suche nach regulären Ausdrücken, wenn man im „Suchen und Ersetzen“-Dialog „weitere Optionen“ öffnet und dort reguläre Ausdrücke aktiviert. Die Online-Hilfe²³ enthält eine Liste der verfügbaren regulären Operatoren.

Kontextfreie Grammatiken – kontextfreie Sprachen (BP: Items 12, 13, 14)

Wie wir auf Seite 10 gesehen haben, können DEA keine beliebig tief geklammerten Ausdrücke erkennen. Da DEA genau die regulären Sprachen erkennen und damit gleich mächtig sind wie reguläre Ausdrücke, können reguläre Ausdrücke also auch keine korrekten Klammerungen beschreiben.

Unmöglicher Arbeitsauftrag: Beauftragen Sie (nach einigen erfolgreich erledigten Aufgaben) Ihre Lerngruppe, korrekte Klammerung ausschließlich mit Hilfe regulärer Operatoren zu beschreiben – die so gewonnene Intuition für die Unmöglichkeit bleibt oft nachhaltiger hängen, als eine formale Begründung.

Wie zu den DEA, gibt es auch zu Kellerautomaten (siehe Seite 11) Grammatiken, die genau deren Sprachen beschreiben: Die kontextfreien Grammatiken. Eine kontextfreie Grammatik darf keine Produktionen mit Kontext enthalten. Ein Gegenbeispiel einer kontextsensitiven (oder „kontextbehafteten“) Produktion wäre etwa

xAy → xabcy

Die Terminale neben A auf der linken(!) Seite der Produktion bedeuten, dass A nur „im Kontext von“ x und y durch abc ersetzt werden darf, sonst aber nicht. Kontextfreie Grammatiken hingegen erlauben nur kontextfreie Produktionen.

Beispiele kontextsensitiver Sprachen wurden auf Seite 13 erläutert.

Extended Backus-Naur-Form (BP: Item 5)

Die EBNF dient als menschen- und maschinenlesbare Schreibweise für kontextfreie Produktionen. Zugunsten des Komforts und einer kompakten Darstellung erlaubt EBNF auch Operatoren ähnlich regulären Ausdrücken, nämlich den Stern * für „das davor beliebig oft“, das Plus für „mindestens einmal“, den senkrechten Strich | für „oder“ sowie Klammerungen.

Die Grammatik für Rechenausdrücke von Seite 16 könnte man etwa so in EBNF übersetzen

Variante 1:
Ausdruck ::= Summand '+' Summand
Ausdruck ::= Summand '-' Summand
Summand ::= '(' Ausdruck ')'
Summand ::= Ausdruck
Summand ::= '0'
Summand ::= '1'
… aber diese Beschreibung kopiert ja nur die Produktionen. Mit EBNF geht es übersichtlicher:

Variante 2:
Ausdruck ::= Summand ( ‚+‘ | ‚-‘ ) Summand
Summand ::= '(' Ausdruck ')'
Summand ::= Ausdruck
Summand ::= '0' | '1'

Die Produktion Summand ::= Ausdruck wurde in die Grammatik eigentlich nur eingefügt, damit beliebig lange Summen („2+3+4+5“) zulässig sind. Aber auch das geht noch einfacher:

Variante 3:
Ausdruck ::= Summand ( ( ‚+‘ | ‚-‘ ) Summand ) +
Summand ::= '(' Ausdruck ')'
Summand ::= '0' | '1'

Wie schon bei Grammatiken und regulären Ausdrücken gibt es auch bei EBNF immer mehrere äquivalente Beschreibungen der gleichen Sprache (wie es auch immer mehrere äquivalente Automaten für eine Sprache gibt).

Variante 3 wird noch einfacher, wenn man auch eine einzelne Zahl als Ausdruck ansieht: Dafür muss man nur das Plus durch einen Stern („mindestens null mal“) ersetzen und kann dann auch auf die zweite Variable verzichten.

Variante 4:
Ausdruck ::= Ausdruck ( ( '+' | '-' ) Ausdruck ) *
Ausdruck ::= '(' Ausdruck ')'
Ausdruck ::= '0' | '1'

Weil jetzt auch einzelne Zahlen erlaubt sind (statt echter Summenterme), handelt es sich allerdings nicht mehr um die gleiche Sprache. Die Varianten 3 und 4 sind also nicht äquivalent.

Syntaxdiagramme (BP: Item 4)

Die meisten Menschen können visuelle Darstellungen leichter auffassen als textuelle. Weil Syntaxdiagramme genau die gleichen Beschreibungsmöglichkeiten bieten wie kontextfreie Grammatiken, eignen sie sich gut für den Aufbau der nötigen intuitiven Vorstellungen; die englische Bezeichnung „railroad diagram“ suggeriert zudem die Interpretation als „Modelleisenbahn“, durch die man mit dem Finger hindurch fährt und dabei nach und nach die Ausgabe erzeugt (bzw. verbraucht); diese enaktive Verwendung ist auch in der Kursstufe oft noch hilfreich.

Der Umgang mit Syntaxdiagrammen wird im Bildungsplan ausdrücklich verlangt. Für eine Einführung mit Übungen bietet sich die (auch sonst empfehlenswerte) Seite www.inf-schule.de²⁴ an; für eigene Syntaxdiagramme stehen im Web Generatoren zur Verfügung²⁵ .

Die Abbildungen 7 und 8 zeigen die Syntaxdiagramme zu zwei der oben erwähnten EBNF-Beschreibungen arithmetischer Ausdrücke.

Weil im Diagramm die Kurvenrichtung der „Weichen“ Bedeutung trägt, sollten Schülerinnen bei der händischen Erstellung von Syntaxdiagrammen sehr sauber zeichnen, damit zweifelsfrei ersichtlich ist, in welche Richtung „das Gleis abbiegt“.

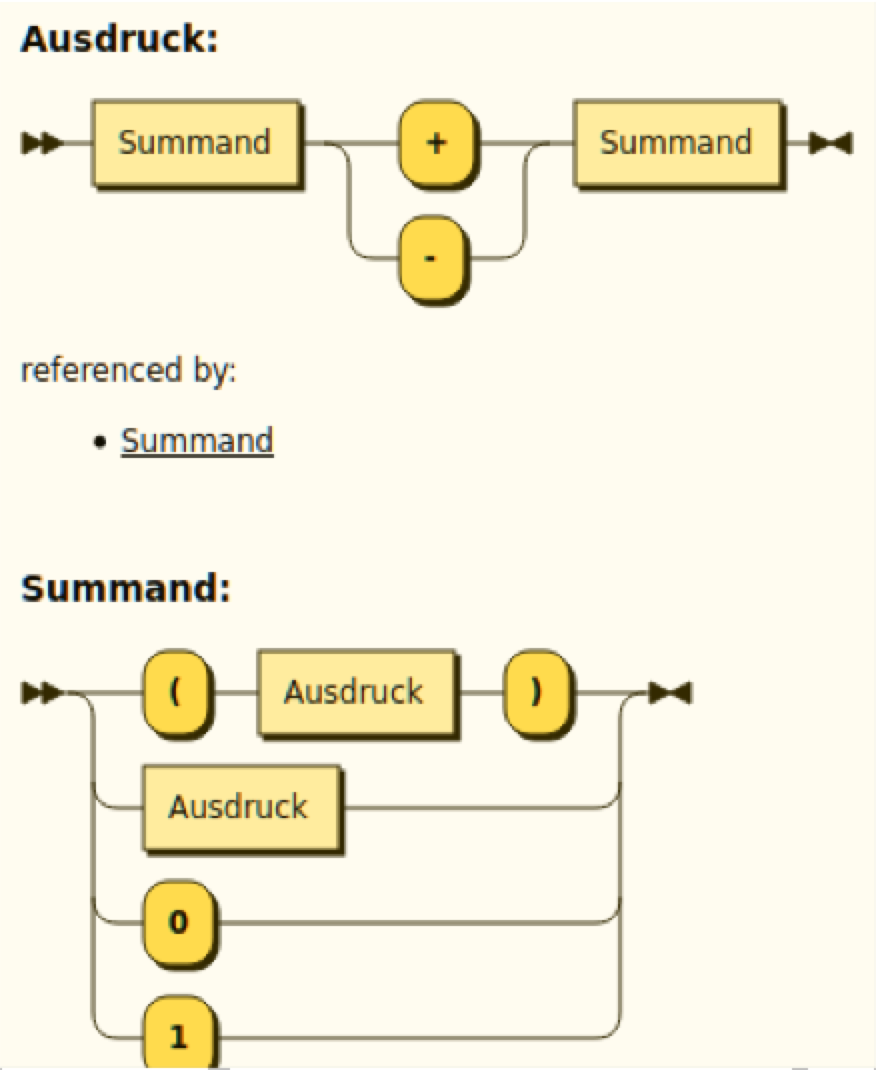
Abbildung 7: Syntaxdiagramm für Rechenausdrücke (zu EBNF Variante 1) ZPG Informatik [CC BY-SA 4.0 DE], aus zpg_sprachenautomaten_hintergrund.odt

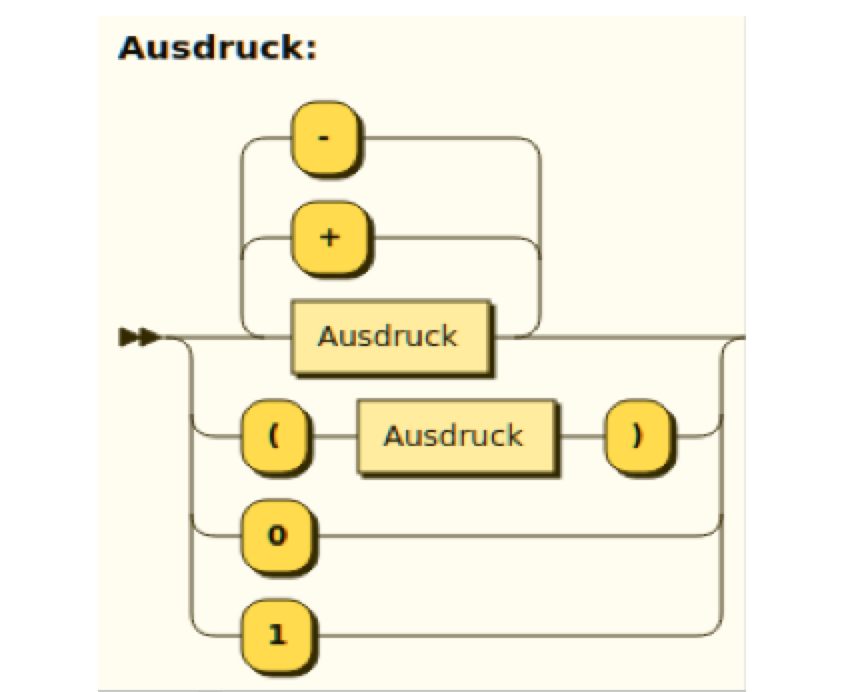
Abbildung 8: Syntaxdiagramm für Rechenausdrücke (zu EBNF Variante 4) ZPG Informatik [CC BY-SA 4.0 DE], aus zpg_sprachenautomaten_hintergrund.odt

Es ist leicht zu begründen, dass Syntaxdiagramme und kontextfreie Grammatiken einander entsprechen und genau gleich mächtig sind, was im Unterricht den Übergang zu einer formaleren Darstellung (EBNF oder Grammatiken) erleichtert:

Es muss ein „Startgleis“ geben, auf dem „die Lok am Anfang losfährt“ (so wie Grammatiken eine Startvariable haben);
Rechtecke stehen für Variablen;
Ovale stehen für Terminale;
Produktionen mit gleicher linker Seite werden mit „Weichen“ zusammengefasst, so wie in EBNF mit dem ODER-Operator | (dem senkrechten Strich).
die rechte Seite eines Syntaxdiagramms darf leer sein („der Zug fährt einfach durch“), so wie es auch leere Produktionen geben kann;
die Überschrift eines Syntaxdiagramms enthält (wie die linke Seite einer kontextfreien Produktion) keine „Bedingung“, also keinen Kontext;
auch der Hinweis auf die Rekursion ist jeweils bei Grammatiken und Syntaxdiagrammen sinnvoll, um dieses wichtige Konzept in unterschiedlichen Zusammenhängen immer wieder zu verankern: Syntaxdiagramme können direkt (ein Gleis enthält sich selber) oder wie im Beispiel indirekt rekursiv sein, genau wie Produktionen einer Grammatik.
Nur die verschiedenen Möglichkeiten, „Weichen“ einzubauen und damit Ausweich- und Wiederholungsmöglichkeiten zu modellieren, gehen über das hinaus, was in Grammatiken im engeren Sinne erlaubt ist. Trotzdem lassen sich alle Syntaxdiagramme in kontextfreie Produktionen umwandeln und umgekehrt.

²¹ Diese Form der Produktionen ist nicht die allgemeine, sondern die für kontextfreie Grammatiken. Weil kontextsensitive Grammatiken aber nicht behandelt werden, halten wir das für ausreichend.

²² Für die automatische Herleitung muss man die kontextfreie Grammatik in einen gleichwertigen Kellerautomaten umwandeln, von dem wir zwar wissen (siehe Tabelle auf Seite 3), dass er tatsächlich existiert; es gibt aber zu jeder Sprache viele Grammatiken, und die meisten davon waren früher nur schwierig umzuwandeln: Man musste die Produktionen zunächst recht mühsam in eine spezielle Form bringen, die die Umwandlung erlaubte. Erst nach 2010 gab es nochmals Fortschritte bei den so genannten „Parsergeneratoren“: Heute kann man aus fast jeder Grammatik vollautomatisch einen Kellerautomaten erzeugen lassen, der die Sprache zu dieser Grammatik erkennt. Der Generator ANTLR etwa erzeugt sehr leistungsfähige Parser mit „adaptivem Lookahead“.

²³ Online verfügbar etwa hier: https://help.libreoffice.org/3.4/Common/List_of_Regular_Expressions/de

²⁴ https://www.inf-schule.de/sprachen/sprachenundautomaten/sprachbeschreibung (Abruf 6.1.2021)

²⁵ Etwa der hier verwendete https://www.bottlecaps.de/rr/ui (Abruf 6.1.2021)

Hintergrundinformationen: Herunterladen [odt][669 KB]

Weiter zu Anwendungen und Beispiele

Sprach­ty­pen und zu­ge­hö­ri­ge Gram­ma­ti­ken (BP: 2, 6, 9-14)

Re­gu­lä­re Gram­ma­ti­ken, re­gu­lä­re Spra­chen (BP: Item 10)

Re­gu­lä­re Aus­drü­cke (BP: Item 10)

Kon­text­freie Gram­ma­ti­ken – kon­text­freie Spra­chen (BP: Items 12, 13, 14)

Ex­ten­ded Ba­ckus-Naur-Form (BP: Item 5)

Syn­tax­dia­gram­me (BP: Item 4)