Konstruktion von geometrischen Figuren

1. Zeichne folgende Geraden:
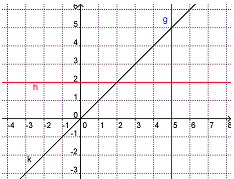
   g: x = 5, h: y = 2, k: y = x
2. Die Geraden g, h und k schließen eine Dreiecksfläche ein. Verschiebe die Gerade h so, dass der Flächeninhalt des Dreiecks größer wird. Gib eine Gleichung für h an.
3. Wie lauten die Gleichungen der Geraden, wenn die Geraden aus Aufgabe 1 an der y-Achse gespiegelt werden?
4. Gib vier Gleichungen von Geraden an, die eine rechteckige Fläche einschließen.
5. Kannst du vier Gleichungen von Geraden finden, die ein echtes Parallelogramm einschließen? Gib die Gleichungen an.
6. Gib vier Gleichungen von Geraden an, die ein echtes Trapez einschließen.
7. Finde weitere Figuren, die durch Geraden begrenzt werden.

Konstruktion von geometrischen Figuren – Lösung

1. 
   
2. Die Gerade h kann nach unten verschoben werden, damit der Flächeninhalt des von g, h und k eingeschlossenen Dreiecks größer wird.
   Zum Beispiel: y = 0
   Oder: Die Gerade h wird so weit nach oben verschoben, dass sie die y-Achse oberhalb von 8 schneidet. Auch dann ist die von g, hneu und k eingeschlossene Fläche größer als die ursprüngliche.
   Zum Beispiel: y = 9
3. Die Gleichungen der Geraden lauten: x = -5 und y = -x. Die Gleichung der Geraden h: y = 2 bleibt gleich.
4. Möglich sind zwei Geraden, die parallel zur x-Achse sind und zwei Geraden, die parallel zur y-Achse sind.
   Zum Beispiel: x = 2, x = 6, y = 1 und y = 5
5. Möglich sind zwei Geraden, die parallel zur y-Achse sind und zwei beliebige parallele Geraden.
   Zum Beispiel: x = 2, x = 5, y = 2x und y = 2x + 4
6. Möglich sind zwei Geraden, die parallel zur y-Achse sind und zwei sich schneidende Geraden.
   Zum Beispiel: x = 2, x = 5, y = 2x + 7, y = -0,5x + 4
7. Zum Beispiel Raute, Quadrat, regelmäßiges Sechseck, ...

Geradenmemory Spiel :    Herunterladen  [doc][69 KB]
Geradenmemory Spiel :    Herunterladen  [pdf][38 KB]