Mittelsenkrechten – Umkreis

Öffne die Geogebra-Datei „ basis_ms.ggb “, um die folgende Aufgabe
zu lösen. Du erkennst ein blaues Dreieck ABC mit den Eckpunkten A,
B und C.

Führe die folgenden Arbeitsschritte der Aufgabe durch und beantworte die Fragen. Dabei helfen dir die Symbole rechts, die du auch im Programm findest.

 

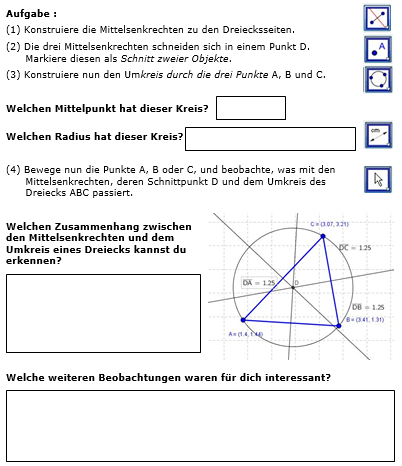
Zusammenhang von Mittelsenkrechten und Umkreis - Lösung

Welchen Mittelpunkt hat dieser Kreis?

D (2,5|1,5)

Welchen Radius hat dieser Kreis?

(ungefähr) 1,58 cm

Welchen Zusammenhang zwischen den Mittelsenkrechten und dem Umkreis eines Dreiecks kannst du erkennen?

Der gemeinsame Schnittpunkt der Mittelsenkrechten eines Dreiecks ist der Mittelpunkt des Umkreises. Sein Radius ist der Abstand des Mittelpunkts zu jedem der drei Eckpunkte.

Welche weiteren Beobachtungen waren für dich interessant?

Mögliche Antworten dieser offenen Fragestellung sind beispielsweise:

• Der Schnittpunkt der Mittelsenkrechten kann außerhalb des Dreiecks liegen.
• Ein Kreis ist durch drei Punkte festgelegt, falls diese nicht auf einer Geraden liegen.
• Liegen die Punkte auf einer Geraden, so sind die Mittelsenkrechten parallel und aus dem Umkreis wird eine Gerade.

  

Nutzung für nicht kommerzielle Zwecke gemäß den Bedingungen unter
http://geogebra.org

 

 

Mittelsenk Um GEO:    Herunterladen  [doc][119 KB]
Mittelsenk Um GEO:    Herunterladen  [pdf][69 KB] 

Geogebra - Dateien
Basis ms:    Herunterladen  [.ggb][6 KB]
Lösung Umkreis:    Herunterladen  [.ggb][10 KB]