Satz des Thales
Anwendung Satz des Thales
|
Liegt der Punkt C eines Dreiecks ABC auf
einem Halbkreis über der Strecke , dann
|
 Mathematisches Problem:
Mathematisches Problem:
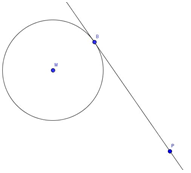
Gegeben sind ein Kreis k und ein Punkt P,
der außerhalb des Kreises liegt.
Gesucht ist ein Punkt B, sodass die Gerade
durch B und P den Kreis in B berührt.
Aufgabe:
Löse das mathematische Problem.
Führe hierzu zuerst die vier unten beschriebenen Konstruktionsschritte mit Hilfe der Geogebra-Datei „
anwendung_thales.ggb
“ durch und beantworte dann die Fragen unter a) bis e).
- Zeichne die Strecke P-M von P zum Mittelpunkt M des Kreises k ein und konstruiere einen Halbkreis h durch die beiden Punkte P und M.
- Markiere den Schnittpunkt von k und h. Nenne diesen B.
- Zeichne das Dreieck mit den Eckpunkten M, B und P ein und bestimme mit einem Geogebra-Befehl die Größe des Innenwinkels bei B.
- Zeichne die gesuchte Gerade durch B und P ein.
a) Wieso muss das Dreieck MPB bei B einen rechten Winkel haben?
b) Warum betrachtet man zunächst einen Halbkreis h durch die beiden Punkte P und M?
c) Wie wird bei der Konstruktion der Satz des Thales angewandt?
d) Kannst du noch einen weiteren Punkt B und damit eine andere Gerade konstruieren, die ebenfalls durch P geht und den gegebenen Kreis berührt?
e) Verschiebe den Punkt P. An welchen Stellen gelingt die Konstruktion nicht?
Anwendung Satz des Thales - Lösung
Illustration der Konstruktionsschritte:
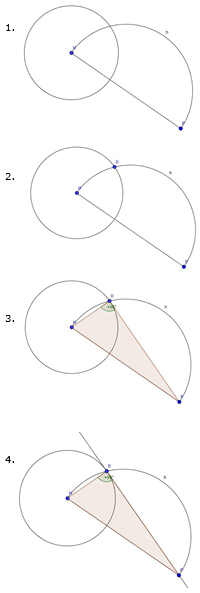
a) Die Gerade durch P und B soll den Kreis k mit Mittelpunkt M in B berühren. Daher muss die Gerade durch P und B senkrecht auf der Geraden durch M und B stehen. Somit muss das Dreieck MPB bei B einen rechten Winkel haben.
b) Ist h ein Halbkreis über den beiden Punkten P und M, so liegt dort ein möglicher Berührpunkt B, denn ...
c) ... der Satz des Thales besagt, dass dann MPB ein Dreieck mit rechtem Winkel bei B ist.
d) Betrachtet man den anderen möglichen Halbkreis über den beiden Punkten P und M, so findet man einen weiteren Berührpunkt und die entsprechende Gerade (siehe Bild unten).
Diese Lösung ist symmetrisch zur ersten Konstruktion.
e) Durch Experimentieren findet man heraus, dass der Punkt P nicht im Kreis k oder auf dessen Rand liegen sollte. Der Punkt P muss also, wie in der mathe-matischen Problemstellung beschrieben, außerhalb des Kreises k liegen.
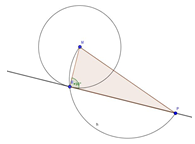
Bild: Symmetrische Lösung
Thales Anw GEO ZF :
Herunterladen
[doc][311 KB]
Thales Anw GEO ZF :
Herunterladen
[pdf][317 KB]
Anwendung Thales: Herunterladen [.ggb][4 KB]
Anwendung Thales Lösung: Herunterladen [.ggb][7 KB]

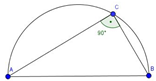 Satz des Thales:
Satz des Thales: