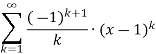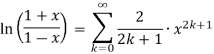Übersicht

Nr

Inhalte

Begleitmaterial

1/2

Einstieg in das Thema Reihen

Definition einer Reihe auf Basis einer Folge

Beispiele für Reihen:

Arithmetische Reihe ; Geometrische Reihe 

Beispiele für geometrische Reihen

Unendliche geometrische Reihe

     (für )

Anwendungen unendlicher geometrischer Reihen:  periodische Brüche

3/4

Divergenz der harmonischen Reihe mithilfe des Minorantenkriteriums

Anwendung des Majorantenkriteriums

Beispiel: 

Leibniz- Kriterium für alternierende Reihen die auf monotonen Nullfolgen basieren

Beispiel:

Auch Rechnereinsatz zur Bestimmung des Grenzwerts (hier: )

5/6

Einstieg Taylorreihe

Wie berechnet ein Taschenrechner Sinuswerte?

Beispiel: f(x) = sin(x)

Gesucht ist ein Polynom p_n(x), zur näherungs-weisen Berechnung von Sinuswerten

Zunächst „übliche“ Methode mit n + 1 Stützstellen (Beispiele: p₃(x) und p₅(x))

Idee von Taylor mit Entwicklungsmitte x₀ = 0.

(n = 3, 5, 7 und 9) (auch grafische Überprüfung)

7/8

Definition des allgemeinen Taylorpolynoms mit der Entwicklungsmitte x₀ = 0. 

Taylorreihe für f mit f(x) = sin(x)

Definition der allgemeinen Taylorreihe mit der Entwicklungsmitte x₀ = 0.

Übung: Taylorreihen für cos(x) und e^x

(auch )

Taylorreihe für f mit f(x) = ln(x)

Entwicklungsmitte x₀ = 1

9/10

Konvergenz von Taylorreihen betrachten

Beispiel:

Weitere Taylorreihen für den natürlichen Logarithmus:

Transformation:

Definition des Konvergenzradius einer Taylorreihe

Anwendung des Wurzelkriteriums und des Quotientenkriteriums zur Bestimmung des Konvergenzradius (nur Mitteilung)

11/12

Übungsaufgaben zu Taylorreihen, teilweise auch mit Bestimmung des Konvergenzradius

Aufgaben zu Taylorreihen