Näherungsverfahren
(1) Intervallverfahren
Liefern durch fortgesetztes Quadrieren die Einsicht, dass eine irrationale Wurzel nicht mit irgendeiner Ziffer enden kann (sie könnte dann aber immer noch periodisch sein).
Sind am Zahlenstrahl einsichtig und gut nachvollziehbar und auf andere Probleme (z.B. Logarithmus) übertragbar. Sind recht schwerfällig (auch im TR).
- Intervallhalbierung
Einstieg: Ich denke mir eine zweistellige Zahl, die Du mit möglichst wenigen Versuchen erraten sollst. Ich sage Dir jeweils, ob Du zu hoch oder zu tief liegst.
Klares Vorgehen, aber sehr langsam:
1
<
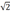
<
2
denn
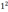
<
2
<
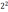
1
<
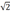
<
1,5
denn
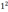
<
2
<
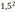
1,25
<
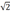
<
1,5
denn
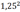
<
2
<
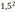
…
- Intervallverfeinerung
Intervall wird in Zehntelschritten quadriert und es werden die beiden Zahlen, deren Quadrate gerade noch unter bzw. über 2 liegen, als neue Grenzen eines Intervalls gewählt. Nun wird das Verfahren in Hundertstelschritten wiederholt.
Mit mehr Grips etwas schneller und damit schülerfreundlicher, aber weniger anschaulich.
1
<
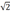
<
2
denn
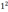
<
2
<
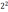
1,4
<
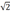
<
1,5
denn
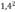
<
2
<
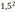
1,41
<
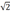
<
1,42
denn
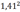
<
2
<
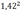
…
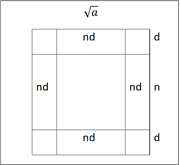
- Wähle (nahe) Quadratzahl
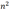 und zeichne zwei zentrumsgleiche Quadrate mit Seitenlängen
und zeichne zwei zentrumsgleiche Quadrate mit Seitenlängen 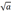 und
und 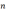 und deren Differenz ist
und deren Differenz ist 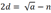
- Die Rahmenfläche r wird durch die vier Rechtecke angenähert:
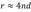
- Also ist
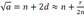 und
und 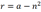
(2) Heron
Näherung erfolgt geometrisch und sehr schnell (auch mit TR). Einsichten am Zahlenstrahl und durch Quadrieren von Näherungswerten bleiben verborgen.
Vorgehen:
Gesucht wird ein Quadrat mit dem Flächeninhalt 2 und damit der Seitenlänge ![]() .
.
Dazu nähert man flächengleiche Rechtecke (mit den Seiten ![]() und
und ![]() ) durch Mittelwertbildung immer weiter an das Quadrat an.
) durch Mittelwertbildung immer weiter an das Quadrat an.
0.Schritt: 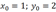
1.Schritt: ![]() (Mittelwert)
(Mittelwert) ![]() (Flächengleichheit)
(Flächengleichheit)
2.Schritt: ![]()
![]() …
…
Insgesamt beruht das Heronverfahren zur Bestimmung von ![]() auf der rekursiven Formel
auf der rekursiven Formel ![]() , die auch leicht im Taschenrechner eingebbar ist.
, die auch leicht im Taschenrechner eingebbar ist.
Für andere Wurzeln ergeben sich auch im zweiten Schritt noch „einfachere“ Zahlen:
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
2 |
3 |
4 |
|
|
1,75 |
|
2,875 |
|
|
1,732142857… |
2,23095238… |
2,654891304… |
Die Formel ist auch ein Spezialfall des Newton-Verfahrens (Spiralcurricularität: Aufgreifen in Oberstufe möglich): ![]()
Nullstellen: ![]()
Auf diese Weise kann man auch eine Näherungsformel für ![]() als Nullstelle von
als Nullstelle von ![]() herleiten:
herleiten:
![]()
Manche höhere Wurzel lässt sich auch mit einer einfachen Übertragung der Heron-formel näherungsweise berechnen:
![]()
Allerdings konvergiert diese Formel langsamer und ab der fünften Wurzeln oft gar nicht.
Definiert man die rechte Seite der Formel als Funktion 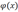 , so ist die Konvergenz
, so ist die Konvergenz
nur für ![]() garantiert.
garantiert.
Beide Formeln lassen sich wieder als Mittelwertbildung diesmal beim Herstellen eines k-dimensionalen Würfel interpretieren. Die einfache Formel verändert dabei eine Kantenlänge und passt die anderen durch Volumengleichheit an. Die schnellere Formel verändert dabei gleich k-1 Kanten gleichzeitig und passt die letzte durch Volumengleichheit an. Der Mittelwert wird dann als gewichtetes Mittel berechnet.
(3) Babylonische Wurzelnäherung
Historisch bedeutsam und dadurch auch historische Ausflüge möglich. Inhaltliche Ausflüge und Rückgriffe möglich (andere Zahlsysteme, 60 als besondere Zahl).
Weniger gut nachvollzieh- und durchführbar (Binnendifferenzierung?!).
Dieses Verfahren lässt sich auch iterieren und ist dabei nicht auf ganzzahlige ![]() oder auf solche, deren Quadrat kleiner als
oder auf solche, deren Quadrat kleiner als ![]() ist, beschränkt:
ist, beschränkt:
Für ![]() gilt n=1 und r=1 und damit:
gilt n=1 und r=1 und damit: ![]()
Und weiter n=1,5 und r=-0,25 und damit: ![]()
Mit diesem Verfahren haben die Babylonier ![]() in ihrem 60er-System verblüffend genau ermittelt und das ca. 1000 Jahre vor Pythagoras:
in ihrem 60er-System verblüffend genau ermittelt und das ca. 1000 Jahre vor Pythagoras:
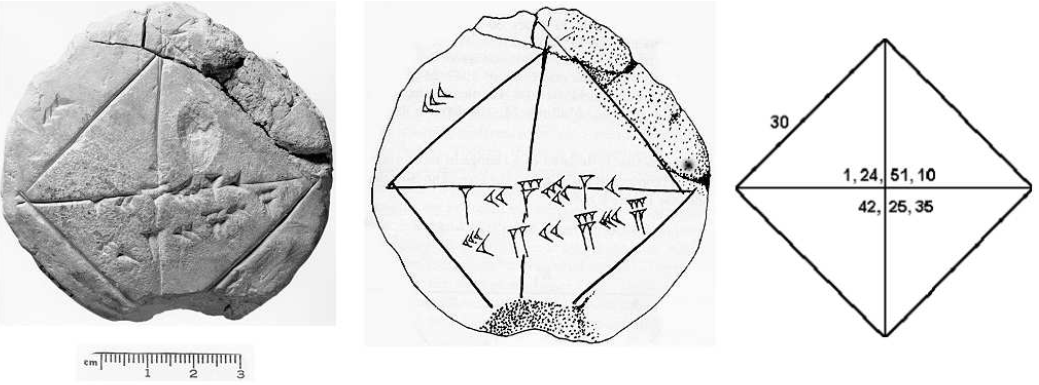
Übersetzung: ![]()
Die Zahlen darunter stellen dann eine ebenso gute Näherung der halben Diagonalenlänge dar.
Artikel: Herunterladen [pdf][1 MB]
Weiter zu Beweisverfahren