Ortskurven erforschen
In der 3. Stunde wird das Konzept der geometrischen Orte in den Mittelpunkt gestellt.
Als übergreifende Idee für den Geometrieunterricht der Sekundarstufen hat sie das Potenzial, den SuS im Sinne Orientierung zu geben und die in verschiedenen Jahrgangsstufen erarbeiteten geometrischen Orte zu vernetzen. Die nachfolgende Übersicht liefert einen guten Überblick1.
| In der Ebene: Menge aller Punkte mit ... | Geometrischer Ort |
|---|---|
| - gleichem Abstand von einem Punkt | Kreis |
| - gleichem Abstand von zwei Punkten | Mittelsenkrechte |
| - gleichem Abstand von zwei Geraden | Winkelhalbierende, Mittelparallele |
| - gleichem Abstand von Punkt und Gerade | Parabel |
| - konstanter Abstandssumme von zwei Punkten | Ellipse |
| - konstanter Abstandsdifferenz von zwei Punkten | Hyperbel |
| - konstantem Abstandsprodukt von zwei Punkten | Cassinische Kurve |
| - konstantem Abstandsquotienten von zwei Punkten | Kreis |
| - gleichem Abstand von Kreis und Punkt im Innern des Kreises | Ellipse |
| - gleichem Abstand von Kreis und Punkt außerhalb des Kreises | Hyperbel |
| Im Raum: Menge aller Punkte mit ... | Geometrischer Ort |
| - gleichem Abstand von einem Punkt | Kugel |
| - gleichem Abstand von zwei Punkten | "Mittelsenkrechten-Ebene" |
| - gleichem Abstand von zwei windschiefen Geraden | "Winkelhalb.-/Mittelparallel-Ebene" |
| - gleichem Abstand von einem Punkt und einer Ebene | Rotationsparaboloid |
| - konstanter Abstandsumme von zwei Punkten | Rotationsellipsoid |
| - konstanter Abstanddifferenz von zwei Punkten | (Zweischaliges) Rotationshyperboloid |
In Aufgabe 1 wird zunächst an das bekannte Vorwissen zu Kreis, Parallelen, Mittelsenkrechte, Winkelhalbierende, In- und Umkreis als geometrische Orte von Punkten mit bestimmten Eigenschaften angeknüpft. In einem ersten Auftrag sollen die SuS in Aufgabenteil a)-f) die verschiedenen geometrische Orte lediglich zeichnen, e) und f) sind dabei als differenzierende Zusatzaufträge gedacht, um unterschiedliche Bearbeitungsgeschwindigkeiten aufzufangen. Nach der Präsentation sollen im zweiten Auftrag dann g) - j) bearbeitet werden. Hierbei wurde ein Gitter hinterlegt, damit die SuS einzelne diskrete Punkte mit einfachen Abstandsüberlegungen lokalisieren können, bevor sie die vermuteten Ortskurven skizzieren. In den Aufgaben wurden nur Parabel und Ellipse eingebunden, um es übersichtlich zu halten. Dabei geht es lediglich um qualitative Skizzen, eine genauere Zeichnung von Parabel, Hyperbel und Ellipse folgt in der zweiten Stundenhälfte in Aufgabe 2.
Möglicher Exkurs: "Laser-Zirkel"

Nach Vergleich und Ergebnissicherung könnte man in einem kurz eingeschobenen Lehrervortrag mit einem rotierenden Laserpointer auf die Wand projizierte Schnittfiguren (Ellipse, Parabel, Hyperbel) visualisieren, um die Frage nach den geometrischen Orten in der Ebene anschaulich zu motivieren. Dies wäre möglich, falls Sie sich im Vorfeld handwerklich betätigen oder innerhalb der Fachschaft hilfsbereite Kolleginnen dafür gewinnen könnten. Falls Sie der Empfehlung folgen und einen Akkuschrauber zu einem modernen "Kegelschnittzirkel" umrüsten möchten, bietet Ihnen die nachfolgende Anleitung dazu Anregungen.

Die Grenzlage der Parabel wird man hierbei natürlich nicht exakt treffen. Vielmehr hat man die Gelegenheit, den fließenden Übergang von Ellipsen zu Hyperbeln dynamisch zu visualisieren und die besondere Grenzlage der Parabel aktiv zu thematisieren. Beim Einsatz bietet es sich an, zunächst nur einzelne Punkte wie im Bild oben rechts zu projizieren und den Akkuschrauber langsam oder von Hand weiterzudrehen. Nach Vermutungen der SuS und ersten Skizzen in den Heften bzw. an der Tafel kann man dann die vollständigen Kegelschnitte projizieren (entgegen den Bildern bitte möglichst in "senkrechter" Lage, d.h. mit der Symmetrieachse nach oben).
Ergänzend könnte man zuvor ggf. noch weitere Rotationskörper als geometrische Orte betrachten, um auf den Doppelkegel hinzuarbeiten, der den Kegelschnitten zugrunde liegt:
"Stelle dir die geometrischen Orte vor und beschreibe sie möglichst anschaulich":
- ein Rechteck rotiert um seine längere Achse → "hoher" Zylinder
- ein rechtwinkliges Dreieck rotiert um eine seiner Katheten → Kegel
- die Gerade g: y=x rotiert um die x-Achse → liegender Doppelkegel mit Öffnungsweite 90°
- zwei Geraden schneiden sich in S, wobei eine um die andere rotiert→ Doppelkegel mit Spitze S
- die Gerade g: y=x rotiert um die y.Achse → senkrechter Doppelkegel mit Öffnungswinkel 90°
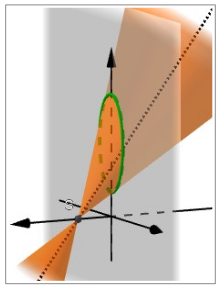
Erste Praxistests haben gezeigt, dass es trotz der eindrucksvollen Visualisierung nicht allen SuS sofort gelingt, sich die Situation räumlich vorzustellen. Da man nur die Schnittfiguren an der Wand, nicht aber den erzeugenden Laserkegel sieht, ist hier eine zusätzliche Visualisierung hilfreich. Falls zur Sichtbarmachung keine Nebenlmaschine zur Verfügung steht, wird die Veranschaulichung des Doppelkegels mithilfe der Datei M10geo03_Gekippter_Kegel.ggb2 empfohlen. Im Gegensatz zum in Stunde 1 eingesetzten Applet "Kegelschnitte" ist hier nicht die Schnittebene, sondern der Doppelkegel drehbar, so dass die verschiedenen Kegelschnitte wie beim echten Experiment an der virtuellen Wand entstehen. Falls der Laserzirkel nicht verwendet wird, kann dieses Applet trotzdem bei der Vorbereitung von Aufgabe 2 unterstützend eingesetzt werden.
In Aufgabe 2 sollen die SuS dann einzelne Punkte von Parabel, Ellipse und Hyperbel in ein vorgegebenes Rasterbild einzeichnen3. Aus didaktischer Sicht reduziert man bei diesem Zugang durch die Diskretisierung (Vorgabe ganzzahliger Abstände mithilfe von Rasterlinien) zunächst die Komplexität. Durch das Betrachten einzelner ausgewählter Rasterpunkte werden dabei die im Fokus stehenden Abstandseigenschaften deutlicher betont als es bei der zusammenhängenden Ortskurve der Fall wäre. Außerdem wird der Vorteil genutzt, dass man durch die zugrundeliegende allgemeine Leitgeradendefinition der Kegelschnitte gleich einen gemeinsamen Zugang zu Ellipse, Parabel und Hyperbel realisieren und gleichzeitig die numerische Exzentrizität ε als Streckfaktor einführen kann: Bei einem Kegelschnitt ist jeder Punkt vom Brennpunkt ε-mal so weit entfernt wie von der Leitgerade.
Die Bearbeitung erfolgt dabei zunächst im a)-Teil für die Parabel, dann folgt im b)-Teil die Zeichnung der leichteren Hyperbel, bevor im c)-Teil durch Einzeichnen der Punkte einer Ellipse deren spannender Entstehensprozess quasi "in Zeitlupe" nachvollzogen wird. Dabei können die SuS den wesentlichen Unterschied erkennen, dass eine Ellipse als geschlossene Kurve im Endlichen liegt, während Äste von Parabeln und Hyperbeln immer ins Unendliche reichen.
Mit Aufgabe 2 ist das Stundenziel erreicht. Die Grundlagen, für die in der Folgestunde mögliche Leitgeradenkonstruktion im Schulhof, stehen zur Verfügung.
Aufgabe 3 bietet die Gelegenheit, Höhenlinien als geometrische Orte zu charakterisieren. Das Applet M10geo03_Hoehenlinien_als_Ortskurven.ggb4 kann bei Bedarf zur dynamischen Visualisierung eingesetzt werden. Hier wurde übrigens die Gleichung einer Trisektrix eingebunden, einer interessanten Kurve, mit der sich wie ihr Name andeutet u.a. auch die Dreiteilung eines Winkels realisieren lässt. Die Aufgabe eignet sich auch als Hausaufgabe.
Aufgabe 4 ist ebenfalls optional und sieht eine vertiefte Auseinandersetzung mit dem Konzept der Rasterbilder und dem Begriff der numerischen Exzentrizität vor. Diese Aufgabe könnte ebenfalls als Hausaufgabe eingesetzt werden, wenn man zuvor den Unterschied zu Aufgabe 2 herausarbeitet. Falls man die Aufgabe im Anschluss an Aufgabe 2 im Unterricht bearbeiten lassen möchte, wäre eine Sicherung zur Unterscheidung der Kegelschnittsarten mit dem abschließenden Merksatz möglich.
Unterrichtsverlauf: Herunterladen [odt][4.8 MB]
Unterrichtsverlauf: Herunterladen [pdf][2.3 MB]
1Quelle: [TIET,200], Kap 4.1: "Geometrische Örter"
2 Das Applet findet man im Materialpaket unter M03_geo/6_GeoGebra-Ergaenzung oder kann es auf der GeoGebra-Seite im Buch "IMP10 für Lehrkräfte" unter https://www.geogebra.org/m/jfeewf5p abrufen.
3Ein Zugang mit Rasterbildern ist u.a. im sehr lesenswerten Artikel "Ellipse, Hyperbel, Parabel – Koordinatengeometrie ohne Vektoren" von Gerald Wittman in ml 133 dargestellt ([WITT], S.50-60).
4 Quelle: [TIET,200], Kap 4.1: "Geometrische Örter"
Weiter zu Ortskurven im Schulhof
