Hüllkurven und Leitkreise
In der optionalen achten Stunde besteht die Möglichkeit, die SuS im Computerraum motivierende Hüllkurven von Ellipsen und Hyperbeln zeichnen zu lassen und danach die Leitkreis-Konstruktion als Ergänzung zur Leitgeraden-Konstruktion kennen zu lernen. Daraus ergibt sich als Vertiefung zu den bisherigen Ortslinien-Defintionen von Ellipsen und Hyperbeln die Leitkreis-Definition als dritte Ortskurvenvariante. Die Stunde ist außerdem so angelegt, dass die SuS alle Dateien selbst erstellen und dabei gleichzeitig ihre Kompetenzen im Umgang mit GeoGebra erweitern können. Vorlagen sind zunächst nicht vorgesehen, könnten aber bei Bedarf ergänzend zur Verfügung gestellt werden1.
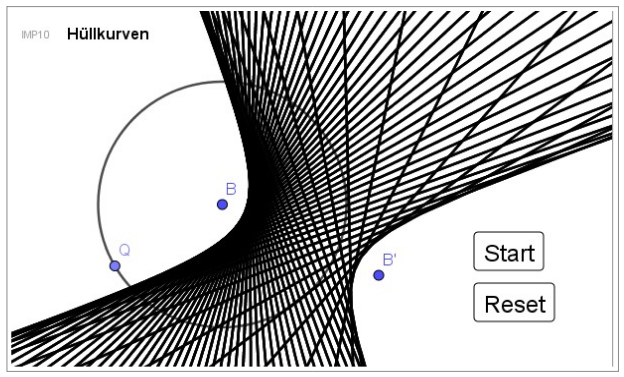
Mit der Anleitung in Aufgabe 1 können mit wenigen Befehlen reizvolle Hüllkurven erstellt werden. Zunächst liegt B innerhalb des Kreises und es entstehen Hüllkurven von Ellipsen. Die SuS variieren dann die Lage des zweiten Brennpunktes B‘ und entdecken den verblüffend einfachen Zusammenhang zwischen den Hüllkurven von Ellipsen und Hyperbeln. Idealerweise konnten sich die SuS zuvor im Rahmen der vorbereitenden Hausaufgabe den Hüllkurven schon enaktiv nähern und bringen ihre gefalteten und gezeichneten Hüllkurven zu Beginn der Stunde mit. Beim Vergleich von Aufgabe 8 kann dann schon vor Bearbeitung von Aufgabe 1 der geometrische Zusammenhang besprochen und geklärt werden, dass die gefalteten Mittelsenkrechten Tangenten an die Kegelschnitte sind.
Auf dieser Basis kann dann in Aufgabe 2 die Leitkreis-Konstruktion in GeoGebra umgesetzt werden. Nach der Konstruktion der Ellipsen und Hyperbeln als Ortskurven kann im vorformulierten b)-Teil die zugrundeliegende Leitkreisdefinition effizient gesichert werden.
Im c) und d)-Teil kann die Brücke zu den bereits aus Stunde 7 bekannten Ortsliniendefinitionen mithilfe der konstanten Abstandssumme (bzw. -differenz) geschlagen werden. Hier besteht nun auch die Möglichkeit, diese geometrisch begründen zu lassen.
Mögliche Vertiefungen: "Reflexion mit Reflexionen"
Aufgabe 3 nimmt die Reflexionseigenschaften aller drei nicht-zerfallenden Kegelschnitte in den Blick, die nun mit Symmetrien begründet werden können. Dieser optionale Exkurs eröffnet gleichzeitig die Möglichkeit einer reflektierenden Gegenüberstellung von Leitgeraden- und Leitkreiskonstruktion im Kontext der physikalischen Reflexionseigenschaften und könnte so zur Abrundung der Einheit verwendet werden. Dabei werden gleichzeitig geometrische Inhalte mit Anwendungen verzahnt und weitere Anknüpfungspunkte aufgezeigt, die bei späteren Gelegenheiten aufgegriffen werden könnten.
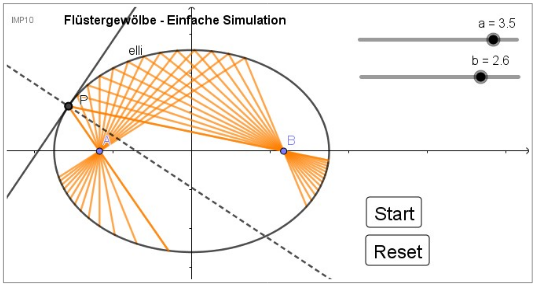
Aufgabe 4 ermöglicht abschließend die Erstellung einer einfachen Simulation zu Flüstergewölben und kann flexibel eingesetzt werden. Wem dieser Kontext nicht zusagt, könnte ggf. auch aus dem Bereich der Medizintechnik das Funktionsprinzip eines Nierensteinzertrümmeres zugrunde legen und eine ggf. leicht modifizierte Simulation erstellen. Gegenüber der in Aufgabe 4 eingebundenen Anleitung wurde das im GeoGebra-Buch der SuS hinterlegte Applet noch um die nicht aus der Ellipse austretenden Strahlen und die Schaltflächen zur Steuerung der Animation erweitert2. Die technische Umsetzung wurde zusätzlich im Erwartungshorizont dokumentiert. Um Resultate wie oben zu erhalten, muss man noch die Eigenschaften des Punktes P anpassen. Unter "Algebra" sollte man die Schrittweite und Geschwindigkeit der Animation erhöhen (z.B. 0.8 und 4).
Unterrichtsverlauf: Herunterladen [odt][4.8 MB]
Unterrichtsverlauf: Herunterladen [pdf][2.3 MB]
1Musterlösungsdateien finden Sie im Materialpaket unter M03_geo/3_vorlagen_tauschordner. Sie wurden als Applets aufbereitet und können auf der GeoGebra-Seite im Buch "IMP10 für SuS" unter https://www.geogebra.org/m/qqfbwvmr abgerufen werden.
2Die Datei findet man im Materialpaket unter M03_geo/3_vorlagen_tauschordner oder kann sie direkt im GeoGebra-Buch IMP10 für SuS unter https://www.geogebra.org/m/qqfbwvmr aufrufen.
Weiter zu Parameterdarstellung von Kurven
