Andere Argumentationsschiene
Hat man natürliche Zahlen n und m gefunden, für die sich das DIN A4 Blatt mit quadratischen Karos randlos bedrucken lässt, so gibt es dazu immer natürliche Zahlen 
<n und 
mit dieser Eigenschaft.
Zu 
, 
gibt es mit der gleichen Überlegung Zahl 
und 
mit dieser Eigenschaft… usw. .
Man erhält unendliche Folge 
und 
natürlicher Zahlen mit dieser Eigenschaft.
Dies aber nicht möglich, da es nur endlich viele natürliche Zahlen kleiner als n und nur endlich viele natürliche Zahlen kleiner als m gibt.
Irrationalitätsbeweis für 
:
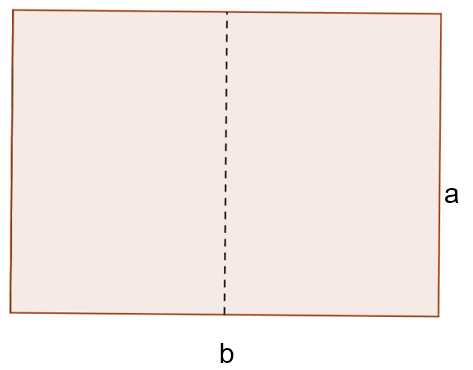
- Bei einem DIN – Blatt gilt für die Seitenlängen
.
Angenommen 
ist eine rationale Zahl.
- Dann muss sich als Bruch darstellen lassen:
,
wobei m und n natürliche Zahlen sind.
- Dann könnte man aber ein DIN – Blatt herstellen mit den Seitenlängen
und 
und dieses Blatt randlos mit n mal m quadratischen Karos mit der Seitenlänge 1 LE überdecken.
Dies aber nicht möglich. Somit kann keine rationale Zahl sein.
Quelle: Christian .Messner
Artikel: Herunterladen [pdf][1 MB]
Weiter zu Material