Info
Potenzieren:
Zahlen, die wiederholt miteinander multipliziert werden.
Definition: Ein Produkt aus gleichen Faktoren kann man als Potenz a n anschreiben.
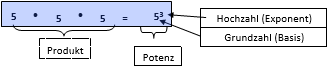Beispiel:
Reihenfolge beim Rechnen
Nach wie vor gilt die Regel:
Punkt - geht vor Strichrechnung
Diese wird jetzt erweitert: "Potenzieren" geht vor "Multiplizieren"
Potenzen mit negativer Basis
Ist die Basis negativ, so unterscheidet man zwei Fälle:
-
Der Exponent ist
gerade
⇒ der Potenzwert ist
positiv:
(-2) 4 = (-2) · (-2) · (-2) · (-2) = 16 -
Der Exponent ist
ungerade
⇒ der Potenzwert ist
negativ:
(-2) 3 = (-2) · (-2) · (-2) = -8
| Potenzrechengesetze: | Allgemein: | Beispiele: |
|
Potenzen werden potenziert, indem man ihre Exponenten multipliziert und die Basis beibehält. Man kann die Exponenten vertauschen. |
|
|
|
Summen oder Differenzen von Potenzen lassen sich nur bei gleicher Basis und gleichem Exponenten vereinfachen. |
|
4a 2 + 5a 2 = 9a 2 4a 2 - 5a 2 = -a 2 |
|
Potenzen mit gleicher Basis werden multipliziert
|
|
2 6 · 2 3 =2 6+3 =2 9 6 5 : 6 3 = 6 5-3 = 6 2 |
|
Potenzen mit gleichen Exponenten werden multipliziert bzw. dividiert, indem man Basen multipliziert bzw. dividiert und die Exponenten beibehält. |
|
2 2 · 6 2 =12 2 10 2 : 5 2 =2 2 |
Ordnen Sie folgende Potenzgesetze in die Tabelle ein. Schauen Sie sich dazu die Beispielaufgaben genau an.
Info herunterladen [doc][41 KB]