Blatt 2 – Die Quadrate
Als Nächstes füllen wir die Reihen mit Quadraten.
7. Schreibe den Rahmen einer Methode zeichneQuadrate(). Stelle darin zunächst schwarz als Füllfarbe ein. (Die Linienfarbe bleibt grau.)
In einer Reihe sollen jeweils acht Quadrate gezeichnet werden, die wieder den Abstand der eigenen Seitenlänge haben.
8. Programmiere das Zeichnen der Quadrate in der ersten Reihe. Nutze wieder eine Zählschleife und nutze auch die Variable s für die Seitenlänge. Das erste Quadrat soll einen Abstand von 10 Pixeln zum Rand haben. Starte dein Programm und ändere deinen Programmcode ab, wenn etwas noch nicht stimmt. (Die Lösung liegt aus.)
In jeder Reihe startet das erste Quadrat aber an einer anderen Stelle. In der ersten, mittleren und letzten Reihe bei 10 Pixeln, jeweils daneben bei 20 und in der dritten und siebten Reihe bei 30 Pixel.
9. Überlege dir, was du für die nächsten Reihen ändern musst.
10. Programmiere das Zeichnen der Quadrate in der zweiten Reihe.
11. Programmiere das Zeichnen der Quadrate in der dritten Reihe.
Vergleiche mit der ausliegenden Lösung und hol dir dann das nächste Blatt.
Es ist sehr umständlich, für jede Reihe eine neue Schleife programmieren zu müssen. Eigentlich wiederholen wir ja wieder neun Mal das Zeichnen einer Reihe von Quadraten.
12. Gib an, was gleich bleibt und überlege dir, was sich ändert. Fülle dazu folgende Tabelle weiter aus:
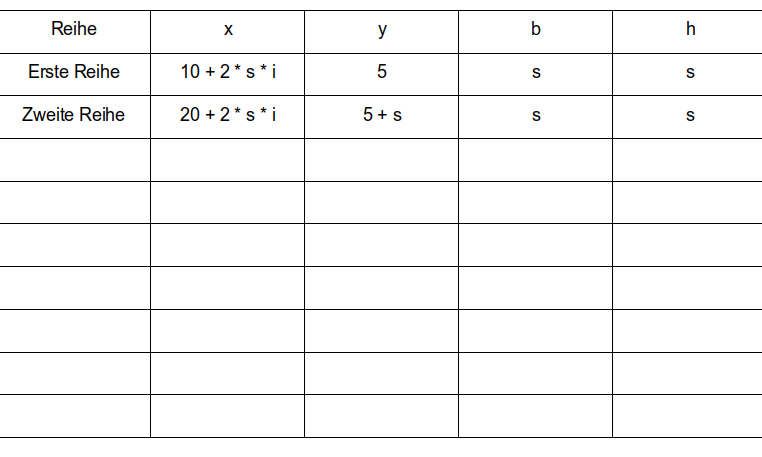
Wir ignorieren zunächst einmal die unterschiedlichen Abstände zum linken Rand und nehmen bei allen Reihen die Zahl 10. Um die Änderung kümmern wir uns später.
Dann ändert sich von Reihe zu Reihe nur die y-Koordinate.
13. Überlege dir, wie du mit einer weiteren Zählvariable j auf die y-Koordinaten kommst. Vergleiche deine Idee mit der ausliegenden Lösung.
Wir bekommen die Quadrate einer Reihe mithilfe einer Zählschleife, die sich in der vereinfachten Form nur in der y-Koordinate unterscheidet.
Da wir aber neun solcher Reihen brauchen, nutzen wir eine weitere Zählschleife, die neunmal unsere bisherige Zählschleife durchläuft.
verschachtelte Zählschleife
Sind zwei oder mehr Zählschleifen ineinander verschachtelt, so nennt man das eine verschachtelte Zählschleife.
Es gibt eine äußere Schleife mit der Zählvariablen j und eine innere Schleife mit der Zählvariablen i.
Die verschachtelte Zählschleife sieht jetzt folgendermaßen aus:

14. Schreibe eine neue Methode zeichneAlleQuadrate(), die diese verschachtelte Zählschleife nutzt. Teste dann dein Programm.
15. Überlege dir jetzt noch einmal ganz genau, was Schritt für Schritt passiert. Wenn es dir noch nicht klar ist, hole dir zur Hilfe das Extrablatt und fülle es Schritt für Schritt aus.
Es wird neunmal nacheinander die innere Schleife aufgerufen, die jeweils acht Quadrate nebeneinander zeichnet.
Leider ist es jetzt keine optische Täuschung mehr, weil wir links immer nur 10 Pixel Abstand lassen.

Statt dem Wert 10 als Abstand zum linken Rand, hätten wir gerne in jeder Reihe einen anderen Wert. Da sich der Wert mal erhöht, mal erniedrigt, können wir ihn nicht durch die Schleifenvariable j darstellen, wie es bei dem Abstand nach oben funktioniert hat.
Feld (Array)
Wir nutzen hier ein sogenanntes Feld (Array), das mehr als einen Wert gleichzeitig speichern kann. Du hast eine solche Datenstruktur schon im letzten Jahr kennen gelernt.
Zur Erinnerung:
Denken wir bei einer Variable an das Schachtelmodell (für jede Variable gibt es eine Schachtel, in der der aktuelle Wert der Variable liegt), können wir uns hier im Vergleich mehrere aneinandergeklebte Schachteln, die durchnummeriert sind, vorstellen.
In unserem Fall würde in den Schachteln jeweils der Abstand zum linken Rand als Wert liegen.
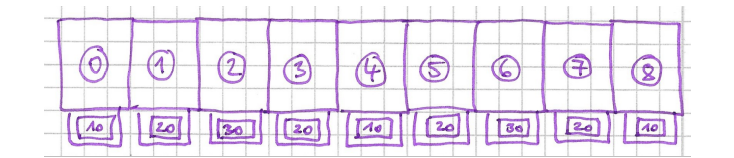
(Eisenmann, ZPG IMP)
In Java müssen wir das Feld bekannt machen und können es auch gleich mit den Werten füllen.
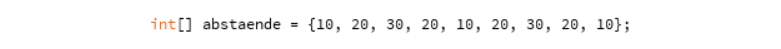
Die beiden eckigen Klammern nach dem Datentyp int zeigen an, dass abstaende ein Feld aus ganzen Zahlen ist.
Der Zugriff auf ein Element des Feldes geht auch mit eckigen Klammern: z.B. liefert abstaende[0] den Wert 10.
16. Ändere dein Programm so ab, dass statt dem Abstand 10 der jeweilige Wert des Feldelementes genutzt wird (alte Zeile: rect() Teste dein Programm und vergleiche mit der Lösung.10+2*s*i,5+j*s,s,s);
Optische Täuschungen: Herunterladen [odt][371 KB]
Optische Täuschungen: Herunterladen [pdf][393 KB]
Weiter zu Verschachtelte Zählschleife
