Ein Zaubertrick: Bezug zur Aufgabe 1

Bildquelle: ZPG IMP [CC BY-SA 3.0 DE]
Der Zauberer mischt 13 Karten so, dass nur er die oberste Karte des Stapels kennt. Nun lässt er einen Zuschauer eine Zahl k zwischen 1 und 10 wählen. Der Zauberer (oder ein Zuschauer) sortiert nun nach und nach immer die oberste Karte des Stapels nach ganz unten (ohne ihren Wert zu betrachten) und zwar genau k Mal. Die dann oben liegende Karte dreht er um. Dies wiederholt man so lange, bis nur noch eine Karte nicht umgedreht auf dem Stapel liegt. Diese Karte wird während des Vorganges vom Zauberer vorhergesagt – es ist die (nur) ihm bekannte Karte, die zu Beginn ganz oben auf dem Stapel lag.
Warum ist das so?
Die Mathematik dazu entdecken die Schülerinnen und Schüler in Aufgabe 1. Die Zahl 13 ist eine Primzahl, also auf jeden Fall teilerfremd zur gewählten Zahl k. Somit werden sicher alle Zahlen durchlaufen (vgl. Aufgabe 1), d.h. hier alle Karten umgedreht. Die erste Karte wird dabei erstmals nach kgV(k;13)-maligem „Nach-hinten-Blättern einer Karte“ wieder erreicht. Bei teilerfremden Zahlen ist dies aber
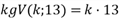
Bildquelle: ZPG IMP [CC BY-SA 3.0 DE]
Kongruenzen und besondere Zahlen: Herunterladen [odt][526 KB]
Weiter zu Kongruenzen bei Codierungen
