Speicherung von Bits
Das RS-Flipflop
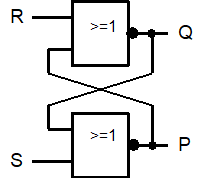
An zahlreichen Stellen in einem Computer müssen binäre Daten für die spätere Weiterverwendung zwischengespeichert werden. Wir wollen uns als erstes mit einer Schaltung vertraut machen, die genau 1 Bit zuverlässig speichern kann. Betrachten wir dazu die folgende Schaltung aus zwei NOR-Gattern:
RS-Flipflop
Um Genaueres über die Funktion dieser Schaltung zu erfahren, ist es sinnvoll, zunächst die Eingänge R auf 1 und S auf 0 zu setzen. Damit ist jedoch noch nicht klar, welche Signale an den Ausgängen Q und P erscheinen werden, weil hier die Ausgangssignale auf die Eingangsseite der Schaltung rückgekoppelt werden: Um zu bestimmen, welchen Wert P hat, müssten wir Q kennen; um aber zu bestimmen, welchen Wert Q hat, müssten wir P kennen. Diese Problematik ist typisch für rückgekoppelte Systeme. Wir müssen also die verschiedenen Möglichkeiten durchprobieren, ehe wir die erste Zeile einer Wahrheitswert-Tabelle für diese Schaltung hinschreiben können.
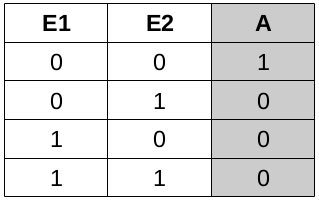
Hier ist zur Erinnerung nochmals die Wahrheitswerttabelle der NOR-Verknüpfung:
NOR-Verknüpfung
Probieren wir die Fälle „Q = 0“ und „Q = 1“ durch:
- Wir nehmen zunächst an, dass Q = 0 sei. Dann „sieht“ das untere NOR-Gatter die Eingangssignale S = 0 und Q = 0. Damit erscheint an seinem Ausgang das Signal P = 1. Das obere NOR-Gatter hat also die Eingangssignale R = 1 und P = 1, was das Ausgangssignal Q = 0 zur Folge hat. Das stimmt aber mit unserer ursprünglichen Annahme überein. Also ist der Zustand „Q = 0 und P = 1“ stabil.
- Nehmen wir hingegen an, dass am Anfang Q = 1 ist, dann hat das untere NOR-Gatter die Eingangssignale S = 0 und Q = 1. Daher produziert es am Ausgang das Signal P = 0. Damit erhält das obere NOR-Gatter die Eingangssignale R = 1 und P = 0. Dies schaltet jedoch den Ausgang Q auf den Wert 0. Wie wir schon unter (a) gesehen haben, führt dies zum stabilen Zustand „Q = 0 und P = 1“.
Egal ob anfangs Q = 0 oder Q = 1 ist, die Schaltung kippt also stets in den Zustand „Q = 0 und P = 1“ und bleibt dann da. Daraus können wir nun die ersten Zeilen einer Wahrheitswert-Tabelle für unsere Schaltung folgern. Die erste Spalte enthält dabei zusätzlich eine Nummerierung der aufeinanderfolgenden Zustände, also quasi eine Zeitleiste:
| t | R | S | Q | P |
|---|---|---|---|---|
| 0 | 0 | 0 | * | * |
| 1 | 1 | 0 | 0 | 1 |
Wenn wir im nächsten Schritt (t = 2) das Eingangssignal R auf 0 zurückschalten, dann ändert sich der Wert von Q dadurch nicht: wegen P = 1 bleibt das obere NOR-Gatter im Zustand Q = 0, so dass der Zustand der Schaltung insgesamt erhalten bleibt:
| t | R | S | Q | P |
|---|---|---|---|---|
| 0 | 0 | 0 | * | * |
| 1 | 1 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 1 |
Im folgenden Schritt (t = 3) setzen wir S = 1. Das untere NOR-Gatter sieht damit die Eingangssignale S = 1 und Q = 0, so dass das Ausgangssignal auf P = 0 kippt. Damit erhält das obere NOR-Gatter die Eingangssignale R = 0 und P = 0, was zu Q = 1 führt. Hierdurch wird jedoch das Ausgangssignal des unteren NOR-Gatters nicht verändert, so dass der Zustand sich stabilisiert. Weiter kann man sich auch hier davon überzeugen, dass der neue Zustand (Q = 1 und P = 0) erhalten bleibt, wenn man das Eingangssignal S auf 0 zurückschaltet (t = 4).
Man erhält also die folgende Tabelle:
| t | R | S | Q | P |
|---|---|---|---|---|
| 0 | 0 | 0 | * | * |
| 1 | 1 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 |
Vergleicht man in der Tabelle die Zeilen t = 2 und t = 4, dann fällt auf, dass in dieser Schaltung die Ausgangssignale Q und P keine Funktion der Eingangssignale R und S sind: zu denselben Eingangsdaten gehören unterschiedliche Ausgangsdaten! Es muss also noch eine andere Variable geben, die den Ausgangszustand der Schaltung mit beeinflusst: wenn man sich die Tabelle nochmals genauer anschaut, sieht man, dass in Q stets die Information vorhanden ist, an welchem der beiden Eingänge R oder S zuletzt eine 1 anlag:
- Ist Q = 0, dann bedeutet dies: die letzte 1 wurde am R-Eingang festgestellt;
- Ist Q = 1, dann bedeutet dies: die letzte 1 wurde am S-Eingang festgestellt.
Mithin hat die Schaltung also ein „Gedächtnis für die letzte 1“. Eine solche Schaltung nennt man ein RS-Flipflop.
Das statische D-Flipflop
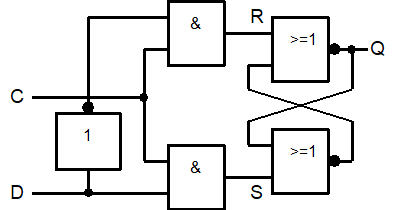
Man kann ein RS-Flipflop zu einem einfachen Speicher für 1 Bit erweitern, welches an einem Dateneingang D ankommt. Die an D anstehende Information wird dem ursprünglichen S-Eingang des Flipflops zugeleitet, die negierte Information (D) dem ursprünglichen R-Eingang. Für die Praxis ist es aber wichtig, dass die Übernahme der Information in den Speicher zu einem wohldefinierten Zeitpunkt stattfindet. Dafür werden die beiden Eingänge R und S mit einer Torsteuerung versehen.
Diese Schaltung nennt man ein (statisches) D-Flipflop. Da der ursprünglich beim RS-Flipflop noch vorhandene Ausgang P stets nur das logische Gegenteil von Q zeigt und somit keine zusätzliche Information liefert, verzichtet man beim D-Flipflop oft auf diesen Ausgang. Der einzige Ausgang ist damit Q. Q enthält immer das gespeicherte Bit, nämlich denjenigen logischen Wert, der an D damals anlag, als C zuletzt den Wert 1 hatte.
„Speichern“ heißt hier also: die D-Information in Q aufbewahren, auch wenn sie an D längst nicht mehr anliegt! Die Information in Q bleibt so lange stabil, wie C = 0 ist. Erst wenn C wieder auf 1 wechselt, wird der dann in D anliegende Wert nach Q übernommen und überschreibt damit den zuvor gespeicherten Wert.
D-Flipflop
Register
Die kleinste Informationsmenge, mit der Programmierer üblicherweise zu tun haben, ist ein Byte, also ein geordnetes Paket aus 8 Bit. Um nun ein Datenregister für z.B. ein solches 8-Bit-Wort zu erhalten, muss man nur 8 D-Flipflops parallel schalten und mit einem gemeinsamen Taktsignal versorgen. Ein entsprechendes 8-Bit-Datenregister wird dann so dargestellt:
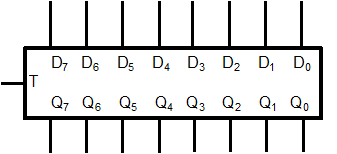
8-Bit Register
Die an den 8 Eingängen D0 bis D7 anliegenden Bits werden durch ein vollständiges Taktsignal am T-Eingang (Wechsel von 0 nach 1 und wieder zurück von 1 nach 0) in die einzelnen Bitspeicher übernommen. Sie stehen dann an den Ausgängen Q0 bis Q7 permanent zur Weiterverarbeitung zur Verfügung, bis durch das nächste Signal am T-Eingang ein neues Datenwort in dieses Register geschrieben wird. Wenn das gespeicherte Datenwort eine (binäre) Zahl darstellt, dann beschreibt der Index die Wertigkeit der einzelnen Bits: der Index 0 gibt dann stets das niederwertigste Bit an („LSB“ = least significant bit), der höchste Index das höchstwertige Bit („MSB“ = most significant bit). Da wir aber üblicherweise mehrstellige Zahlen mit nach links zunehmender Stellenwertigkeit schreiben, wurden die Eingänge hier von rechts nach links ansteigend durchnummeriert.

8-Bit Register
Hintergrundinformationen: Herunterladen [odt][4 MB]
Weiter zu Verknüpfung binärer Datenworte
