Registermaschine
Die Registermaschine (engl. random access machine) ist ein Rechnermodell der theoretischen Informatik, das einem realen Rechner (PC) sehr ähnlich ist. Dabei gibt es verschiedene Definitionen einer Registermaschine, die sich vor allem im Umfang der zulässigen Operationen unterscheiden. Die hier vorgestellte Registermaschine stammt aus dem Bereich der Komplexitätstheorie. Man verwendet sie, um die Komplexität, d.h. den Zeitbedarf von Algorithmen abschätzen zu können, ohne sich auf ein spezielles Computermodell zu beziehen. Da man beweisen kann, dass die Registermaschine und die Turingmaschine in Bezug auf die Berechenbarkeit gleichwertig sind, kann man davon ausgehen, dass alles, was überhaupt berechenbar ist, sich mit einer Registermaschine berechnen lässt. Die Registermaschine kann damit alles, was ein realer Computer auch kann, obwohl sie sehr einfach gebaut ist und nur wenige Befehle beherrscht.
Die Registermaschine besteht formal aus
-
einem Programm bestehend aus endlich vielen durchnummerierten Befehlen
-
einem Befehlszähler b
-
einem Akkumulator c(0)
-
und einem unendlich großem Speicher aus durchnummerierten Speicherzellen (Register) c(1), c(2), c(3), …
Alle Register (incl. b und c(0)) enthalten beliebig große natürliche Zahlen. Das Programm besteht aus Befehlen zum Übertragen der Registerwerte in andere Register, Befehle für die Grundrechenarten und Sprungbefehlen, um an eine andere Stelle im Programm zu springen.
Die Registermaschine führt die Befehle des Programms nacheinander aus. Es wird immer der Befehl mit der Nummer b ausgeführt. Fast alle Befehle erhöhen dabei den Befehlszähler um 1, so dass der nächste Befehl ausgeführt wird. Nur die Sprungbefehle setzen b auf einen anderen Wert, um an eine andere Stelle im Programm zu springen. Die Registermaschine endet, sobald sie auf den Befehl HALT trifft. Das Ergebnis der Berechnung steht dann in (zuvor) definierten Registern.1
Dieses Modell entspricht weitgehend dem Aufbau eines realen Rechners:
Den Befehlszähler, den Akkumulator und einige der Speicherzellen findet man im Prozessor. Der Prozessor besteht aus einem Rechenwerk und einem Steuerwerk. Das Rechenwerk enthält die ALU (arithmetic logic unit) und einige Hilfs- und Statusregister. Die ALU ist in der Lage einfache logische Verknüpfungen und die Grundrechenarten durchzuführen (vgl. Kapitel „Verknüpfung binärer Datenworte“). Der Akkumulator (wird mit AX bezeichnet) ist eines der Hilfsregister im Prozessor. Darüber hinaus enthalten reale Prozessoren weitere Speicherzellen, die nicht unbedingt notwendig sind, aber die Ausführung der Befehle beschleunigen. Die Core i-Prozessoren besitzen beispielsweise 16 Register mit 64 Bit Breite, Itanium-Prozessoren sogar 128 Register mit 64 und weitere 128 Register mit 82 Bit.
Im Statusregister werden Informationen (Flags) über das Ergebnis der letzten Berechnung abgelegt: War das letzte Ergebnis 0 (Zero-Flag)? War das Ergebnis negativ (Sign-Flag)? Diese Informationen werden für den weiteren Programmablauf benutzt, um bedingte Sprünge zu anderen Programmstellen auszuführen.
Die restlichen Speicherzellen der Registermaschine stellen den Arbeitsspeicher (RAM) des Computers dar. In einem realen Computer sind alle Speicherzellen natürlich nicht beliebig groß, sondern können nur Zahlen bis zu einem gewissen Maximalwert aufnehmen. Im Gegensatz zur formalen Definition, bei der Daten und Programm getrennt sind, liegt auch das Programm für die Registermaschine im Arbeitsspeicher.
Das Steuerwerk verwaltet den Befehlszähler und sorgt dafür, dass die zur Verfügung stehenden Befehle in die richtigen Schaltimpulse für die ALU umgesetzt werden. Der Befehlssatz eines realen Rechners umfasst alle Befehle, die für die Registermaschine definiert sind. In der Regel beherrscht er aber einige mehr.
Von-Neumann-Architektur
Diese Architektur wurde schon 1945 von John von Neumann vorgeschlagen. Seine entscheidende Idee aber war es, nicht nur die Daten, sondern auch das Programm der Registermaschine im Arbeitsspeicher abzulegen. Nur dadurch wird der reale Computer zu einer universellen Maschine. Dies ist für das mathematische Modell der Registermaschine unerheblich, da es hier nur um Laufzeitabschätzungen und keine konkrete Umsetzung geht, und findet daher keine Berücksichtigung in der Definition.
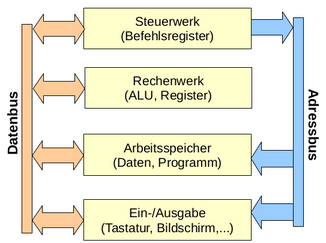
Von Neumann Architektur
In einem realen Prozessor sorgt ein Bussystem für die Übertragung der Daten zwischen dem Arbeitsspeicher (und weiteren Rechnerkomponenten) und dem Prozessor. Die Kommunikation des sehr schnellen Prozessors mit hohen Taktraten mit dem vergleichsweise langsamen Arbeitsspeicher ist nicht unproblematisch und kann den Prozessor ausbremsen. Das Bussystem wird daher auch als Von-Neumann-Flaschenhals bezeichnet. In den Anfangsjahren der Computer war der Prozessor das langsamste Bauelement, so dass die Nutzung eines einzigen Busses für die Datenübertragung von Daten und Programmbefehlen kein Problem war. Inzwischen sind die Prozessoren aber um ein Vielfaches schneller als das Bussystem. Daher werden zahlreiche Maßnahmen ergriffen (L2-Cache-Speicher = schneller Speicher im Prozessor; Vorhersage von Speicherzugriffen, um die Daten schon vorher zu laden; usw.), um die Auswirkungen zu begrenzen. Im Folgenden wird nur das Pipelining angesprochen.
Wenn die Programme sich genauso wie die Daten im Arbeitsspeicher befinden, müssen die einzelnen Befehle vor der Ausführung in den Prozessor übertragen werden und dort in die Schaltimpulse für die ALU übersetzt werden. Der Von-Neumann Zyklus beschreibt diesen Vorgang:
FETCH

Von Neumann-Zyklus
In das Befehls-Register (OP = Operation Pointer) wird aus dem Arbeitsspeicher der Maschinencode des nächsten zu bearbeitenden Befehls geladen.
Bei modernen Prozessoren können mehrere Befehle (etwa 10-20 Befehle) aus dem Speicher in einen Zwischenspeicher (Prefetch-Registerblock) geladen werden, während der aktuelle Befehl noch decodiert wird (OpCode Prefetching). Dies wird als Pipelining bezeichnet.
-
Vorteil: Deutliche Steigerung der Verarbeitungsgeschwindigkeit.
-
Nachteil: Bei Programmverzweigungen müssen Befehle evtl. wieder entfernt werden.
DECODE
Der Befehl aus dem OP-Register wird durch das Steuerwerk in Schaltinstruktionen für das Rechenwerk aufgelöst. Dabei muss ein einzelner Befehl in ganze Sequenz von Steuersignalen übersetzt werden. Eine einfache und bewährte Möglichkeit ist die Speicherung der Abläufe in einem ROM-Baustein (Read-Only-Memory). Welche Speicherstelle des ROM ausgelesen wird, wird durch das OP-Register, den Zustand des Statusregisters (Flags) und durch Einstellungen im ROM-Baustein selbst festgelegt. Jede Ausgabe von Steuersignalen führt zu einem Wechsel auf eine neue Adresse, so dass sich eine Sequenz von Steuersignalen ergibt. Durch eine geeignete Auswahl der Folgeadresse sind auch Wiederholungen und Verzweigungen möglich. Man spricht daher von Mikroprogrammierung und bezeichnet den Speicherbaustein als Mikroprogrammspeicher (Mikrocode-ROM)2.
FETCH OPERANDS
Aus dem Arbeitsspeicher werden nun die Operanden geholt, d.h. Werte, die als Parameter verwendet werden.
Moderne Prozessoren (z.B. Intel Core) kennen das „spekulative Laden“: Das Steuerwerk startet das (möglicherweise) langwierige Laden von Operanden, sobald in der Pipeline ein Ladebefehl auftaucht. Wird nun vorher ein Schreibbefehl ausgeführt, der diese Daten verändert, müssen die zu früh geladenen Daten verworfen und erneut geladen werden. Im Durchschnitt wird die Verarbeitung dadurch aber beschleunigt3.
EXECUTE
Die Sequenz von Schaltimpulsen wird vom Rechenwerk ausgeführt. Eine einzelne Steueranweisung kann dabei mehrere Taktzyklen benötigen. Ein ganzer Maschinenbefehl, also die ganze Sequenz von Steuersignalen, benötigt in der Regel also viele Takte.
UPDATE PROGRAM COUNTER
Der Befehlszähler (IP = Instruction Pointer) muss erhöht werden, damit er auf den nächsten Befehl im Arbeitsspeicher zeigt.
Jetzt kann der Zyklus wieder von vorn beginnen.
Registermaschinen-Simulator
Das mathematische Modell kann – ergänzt um das Bussystem – in einem Simulationsprogramm umgesetzt werden. Alle dabei benötigten Komponenten bestehen aus einfachen elektronischen Schaltungen, die in den vorangegangen Kapiteln besprochen wurden.
Die ALU enthält die logischen Verknüpfungsoperationen und einfache mathematische Funktionen. Für viele Anwendungen reichen Additions- und Subtraktionsschaltungen. Die Register können durch FlipFlops realisiert werden. Das Bussystem kann durch eine einfache Torsteuerung simuliert werden.
Damit kann aus einfachen Bauelementen ein Simulator aufgebaut werden, der theoretisch jedes berechenbare Problem lösen kann. Die Begrenzung des Arbeitsspeichers im Simulationsprogramm stellt dabei eine notwendige Einschränkung eines realen Programms dar. Die Registermaschine ist damit zwar keine universelle Maschine mehr, kann aber trotzdem eine Vielzahl von Problemen lösen.
Eine weitere Einschränkung stellt die Beschränkung der Registerbreite auf eine feste Bitzahl dar. Durch diese Einschränkung, die auch für reale Computer gilt, können nicht beliebige große Zahlen gespeichert werden, sondern nur bis zu einem gewissen Maximalwert. Dies hat Auswirkungen bei der Verwendung von Variablen beim Programmieren, die notwendigerweise immer einen beschränkten Wertebereich haben (vgl. Lösung Mikrosim-Skript Aufg. 1k). Addiert man zum Maximalwert 1 hinzu, landet man beim kleinstmöglichen Wert (vgl. 2-er Komplementdarstellung). Solche Überläufe sind im mathematischen Modell der Registermaschine nicht vorgesehen.
Der Befehlssatz der Registermaschinen-Simulatoren umfasst in der Regel in etwa den Befehlssatz, der für das Registermaschinenmodell in der Komplexitätstheorie definiert wird. Ein Maschinenbefehl besteht dabei aus einem Operationsteil und einem Operandenteil.
-
Der Operationsteil gibt die Einsprungstelle im Mikroprogrammspeicher an. Da diese Adressen schwer zu merken sind, werden ihnen eine Befehlsbezeichnungen, wie add für addieren oder mov für Datentransfer zugeordnet. Diese Befehlsbezeichnungen bilden eine Assemblersprache.
-
Der Operandenteil beinhaltet den Operand als direkten Wert (z.B. 05) oder als RAM-Adresse (Darstellung mit eckiger Klammer z.B. [05]). Dabei beschränkt man sich auf einen Operand. Die Arbeit mit (maximal) 1-Operand-Befehlen hat zur Folge, dass zweistellige Operationen ein fest definiertes Register als weiteren Operand verwenden und das Ergebnis an der Stelle des ersten Operanden speichern.
z.B. ADD AX, 05 => Die Zahl 05 zu AX addiert und das Ergebnis wieder in AX gespeichert. AX ist hier kein Operand, sondern Teil der Operation. ADD BX, 05 ist also eine andere Operation. Dadurch erreicht man die Beschränkung auf 1-Operand-Befehle.
Die Registermaschine definiert Befehle zur Übertragung zwischen Registern und Arbeitsspeicher, einfache Rechenoperationen (Inkrement, Dekrement, Addition, Subtraktion, Multiplikation, Division) und Sprungbefehle, die den Programmablauf beeinflussen. In vollständigen Assemblersprachen gibt es daneben noch Befehle für den Aufruf von Unterprogrammen, Stack-Befehle (ein Stapel erleichtert die Auswertung von Termen), Befehle zum Aufruf von Betriebssystem-Befehlen, uvm.
Viele Befehle existieren in zwei Versionen: z.B. MOV AX, BX und MOV AX,[BX]. Die erste Variante überträgt den Wert von BX nach AX. Die zweite Variante überträgt den Wert aus dem RAM, der an der Adresse BX steht. Sie ist hilfreich, um ein Array zu realisieren. Das BX-Register kann hochgezählt werden und damit auf eine Reihe von aufeinanderfolgenden Speicheradressen zugegriffen werden.
Die Sprungbefehle beeinflussen weder den Wert der Hilfsregister noch den RAM. Sie sind dazu gedacht den Programmauflauf zu steuern. Da der nächste auszuführende Befehl im Befehlsregister des Steuerwerks (IP = Instruction Pointer) steht, muss dazu lediglich dieses Register angepasst werden. In Abhängigkeit der Statusregister können dabei bedingte Sprünge ausgeführt werden, d.h. Sprünge, die nur dann ausgeführt werden, wenn ein bestimmtes Flag gesetzt ist, bzw. nicht gesetzt ist. Die wichtigsten sind
-
JZ = Sprung, wenn das Zero-Flag gesetzt ist, d.h. das Ergebnis der letzten Berechnung Null ergeben hat
-
JNZ = Sprung, wenn das Zero-Flag nicht gesetzt ist.
-
JS = Sprung, wenn das Sign-Flag gesetzt ist, d.h. das Ergebnis der letzten Berechnung negativ ist (d.h. das erste Bit gesetzt ist)
-
JNS = Sprung, wenn das Sign-Flag nicht gesetzt ist.
1 Definition der Registermaschine aus Seite Registermaschine. In: Wikipedia, Die freie Enzyklopädie. Bearbeitungsstand: 22. August 2011. (Abgerufen: 24. September 2011)
2 Wüst, Klaus: Mikroprozessortechnik: Grundlagen, Architekturen und Programmierung von Mikroprozessoren, Mikrocontrollern und Signalprozessoren, Vieweg+Teubner, S.91
3 Wüst, Klaus: Mikroprozessortechnik: Grundlagen, Architekturen und Programmierung von Mikroprozessoren, Mikrocontrollern und Signalprozessoren, Vieweg+Teubner, S.212
Hintergrundinformationen: Herunterladen [odt][4 MB]
Weiter zu Programmierung
