Projekt Pythagoras: Anlage der Studie
Infobox
Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Bitte beachten Sie, dass der Bildungsplan fortgeschrieben wurde.
Ich beginne mit einigen Ergebnissen aus einem von der Deutschen Forschungsgemeinschaft geförderten Forschungsprojekt, das über sechs Jahre lang Teil des Schwerpunktprogramms „Bildungsqualität von Schule“ war [1] , und das ich gemeinsam mit Kollegen und einigen Mitarbeitern der Universität Zürich durchgeführt habe. Irgendwann haben wir ihm den schönen Namen „Projekt Pythagoras“ gegeben, weil wir über ein Schuljahr hinweg Mathematikunterricht untersucht haben: Mit Befragungen und Tests, in denen wir das Vorwissen am Anfang des Schuljahres und die Leistung am Ende des Schuljahres, aber auch die Interessenentwicklung und Hintergrundvariablen, wie z. B. soziale Herkunft, erhoben haben.
Das Besondere dieser Studie war, dass im Laufe des Schuljahres in jeder der 40 beteiligten Klassen zwei Unterrichtseinheiten mit jeweils zwei bis drei Stunden zum Thema „Einführung in die Satzgruppe des Pythagoras“ videographiert wurden. Wir haben die Lehrkräfte gebeten, uns genau dann zu rufen, wenn sie mit dieser Satzgruppe anfangen, weil wir wissen, dass die Satzgruppe des Pythagoras ein neuralgischer, aber auch ein besonders interessanter Punkt aus der Schulmathematik ist, sowohl vom fachlichen als auch vom fachdidaktischen Standpunkt aus gesehen. Es ist der Punkt, an dem sich Algebra und Geometrie am Deutlichsten verknüpfen, und deshalb braucht man sowohl algebraische als auch geometrische Voraussetzungen. Es ist der Punkt, an dem dann typischerweise auch ein Beweis geführt wird, wenn er nicht schon vorher z. B. beim Basiswinkelsatz eingeführt wurde. Spätestens beim „Pythagoras“ muss man an Gymnasien und Realschulen einen Beweis bringen. Und genau das wollten wir auch sehen. Wir haben die Lehrerinnen und Lehrer gebeten, in ihren zwei bis drei Unterrichtsstunden mindestens einen Beweis unterzubringen. Dadurch haben wir eine Vergleichschance, die man in anderen Videostudien nicht hat; in anderen Videostudien wurde mehr oder weniger Zufälliges aufgenommen wurde, so etwa bei TIMSS.
Unsere Stichprobe bestand aus 20 deutschen Klassen und 20 Schweizer Klassen unterschiedlicher Jahrgänge (8. und 9. Klassen). Uns war wichtig, dass die Themen auch im Curriculum auftauchten; wir kontrollierten stets etwaige Unterschiede zwischen den Ländern, achteten aber auch darauf, dass die analysierten Situationen vergleichbar waren.
Worauf zielen wir ab, wenn wir die Vermittlung des Pythagoras untersuchen? Wir zielen nicht auf mathematische Kompetenz generell ab, sondern wir versuchen, diese Kompetenz etwas feiner zu erfassen. Einer der Vorteile der Bildungsstandards der Kultusministerkonferenz ist, dass sie nicht von mathematischer Leistung insgesamt sprechen, also nicht einen eher schlichten Standardbegriff haben, der sich ausschließlich an Testleistungen orientiert, wie beispielsweise in den USA. Die Publikation der Kultusministerkonferenz geht anders vor: Sie verankert Standards in etwas, das sie „Kompetenzmodell“ nennt. D. h. hinter den Bildungsstandards steht idealer Weise eine komplexere Vorstellung davon, was denn eigentlich die Teilkomponenten von – in diesem Fall – mathematischer Kompetenz sind und wie die Graduierungsstufen zu beschreiben sind.
Im Bezug auf Pythagoras haben wir zwei zentrale Teilkomponenten unterschieden. Allein diese auch psychometrisch sauber zu unterscheiden, war schon eine Herausforderung. Die eine Teilkomponente nenne ich „Anwendungsfähigkeiten“ .
5. Anna baut aus Holz ein Vogelhaus. Sie hat einen Plan gezeichnet, auf dem
die Dicke des Holzes vernachlässigt ist. Der Plan sieht so aus:
(Zeichnung nicht maßgenau)
20 cm
 15 cm
15 cm
15 cm
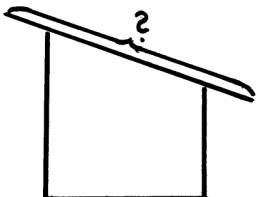
Das Dach soll auf beiden Seiten 5 cm über die Wände hinausragen. Anna will nun ausrechnen, wie lang das Holzbrett für das Dach sein muss. Wie würdest Du vorgehen?
Hier sehen Sie eine typische Textaufgabe, eine Anwendungsaufgabe, wie sie mit dem Satz des Pythagoras verbunden ist. Die Schülerinnen und Schüler sollen berechnen, wie lang die Schräge des Daches mindestens sein muss. In irgendeiner Weise muss man hier den Satz des Pythagoras anwenden, um die Aufgabe zu lösen. Das ist die klassische mathematische Kompetenz, die typisch für den deutschen Mathematikunterricht ist. Das ist jedoch noch nicht das, was die PISA-Kollegen „modellieren“ nennen, sondern es ist „anwenden“, anwenden in einem Alltagskontext.
8. Silvia, Jens und Frank haben versucht, den Satz des Pathagoras zu beweisen.
Wie beurteilst Du die Lösungen der vier Schüler?
Satz des Pythagoras:
Im rechtwinkligen Dreieck mit den Katheten a und b und der Hypothenuse c gilt:
a² + b² = c².
Silvias Antwort:
|
Aussage: |
Begründung: |
||||
|
|
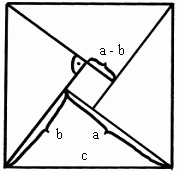
Das große Quadrat hat die Fläche c². Es setzt sich aus dem kleinen Quadrat mit der Fläche (a - b)² und den 4 Dreiecken zusammen. |
||||
|
(1) |
c² = (a – b) ² + 4 x |
a · b
|
Jedes der Dreiecke hat die Fläche |
a · b
|
|
|
(2) |
c² = a² - 2ab + b² + 4 · |
a · b
|
Nach binomischer Formel ist (a - b)² = a² - 2ab + b² |
||
|
(3) |
c² = a² - 2ab + b² + 2ab |
Umformung von (2) |
|||
|
(4) |
c² = a² + b² |
- 2ab + 2ab = 0 |
|||
|
Die Behauptung ist also wahr! |
|||||
|
Beurteilung von Silvias Lösung: Silvias Lösung ... |
ja nein |
||||
|
... enthält einen Fehler. |
□ □ |
||||
|
... zeigt, dass die Behauptung für alle
|
□ □ |
||||
|
... zeigt, dass die Behauptung für bestimmte
|
□ □ |
||||
|
... ist geeignet, um die Behauptung jemandem
|
□ □ |
||||
Wie Sie der zweiten Aufgabe entnehmen können, haben wir im Kontrast zu den Anwendungsfähigkeiten das „Beweisverständnis“ untersucht, weil wir denken, dass hierin ein wesentliches Ziel mathematischer Bildung besteht. Darin sehen Sie auch einen Bildungsanspruch, der über das bloße Anwenden von Mathematik hinausgeht. Ein Bildungsziel des Mathematikunterrichts müsste es sein, das Beweisverständnis der Schülerinnen und Schüler zu fördern. Das heißt sehr viel: zum Beispiel überhaupt die Motivation für einen Beweis zu erkennen. Warum muss ich denn in der Mathematik eigentlich etwas beweisen? Warum reicht es nicht, wenn ich 50 passende Beispiele gesehen habe?
Diese Fragen haben wir mit einer Aufgabe geprüft, die ich zusammen mit Frau Reiss, einer Mathematikdidaktikerin, aus einer englischen Studie adaptiert habe. Die Idee ist die folgende: Es werden drei unterschiedliche Beweise vorgestellt, die eher formal oder narrativ aufgebaut sein können und die richtig oder falsch sein können. Die Schüler müssen diese Beweise beurteilen. Wir sehen dabei, dass Schülerinnen und Schüler Beweise oft schlichtweg danach beurteilen, ob sie in formaler Hinsicht schön aufgebaut sind. Das heißt: Wenn es so aussieht, als sei alles Schritt für Schritt sauber aufgeschrieben, dann finden die Schülerinnen und Schüler, dass ein guter Beweis vorliegt, mit dem sie auch argumentieren könnten. Dass dieser Beweis vielleicht tautologisch ist, erkennen sie gar nicht. So etwas zu überprüfen, zeichnet unseren Test zum Beweisverständnis aus.
Wir haben 40 Klassen im Längsschnitt untersucht. So können wir jede Klasse danach einordnen, wie stark sie im Verlauf der Unterrichtseinheit auf diesen Leistungsdimensionen die Kompetenz erweitert hat.
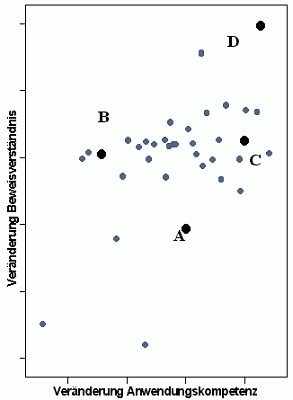 Auf
der X-Achse dieser Abbildung ist die Veränderung in der Anwendungskompetenz
dargestellt, d. h., wie stark im Verlauf dieser Unterrichtseinheit zur Satzgruppe
des Pythagoras die generelle, unterrichtstypische Fähigkeit angestiegen ist,
diesen Satz in verschiedenen Kontexten anzuwenden. Auf der vertikalen Achse,
der Y-Achse, ist abgetragen, wie sich das Beweisverständnis verändert. Sie sehen,
hier gibt es eine ziemliche Streuung. Wir haben links unten eine Schulklasse,
die in beiderlei Hinsicht ziemlich schlecht abschneidet. Die Ursachen sind vielfältig:
Das ist z. B. eine Lerngruppe, die unter äußerst schwierigen Bedingungen in
einer Metropole mit hohem Migrationsanteil arbeitet. Die Streuung tritt auf,
obwohl es sich nur um Gymnasial- und Realschulklassen handelt, es ist keine
Hauptschulklasse dabei. Rechts oben haben wir ein Beispiel, bei dem es in exzellenter
Weise gelingt, in beiden Dimensionen sehr gute Leistungsfortschritte zu erbringen.
Auf
der X-Achse dieser Abbildung ist die Veränderung in der Anwendungskompetenz
dargestellt, d. h., wie stark im Verlauf dieser Unterrichtseinheit zur Satzgruppe
des Pythagoras die generelle, unterrichtstypische Fähigkeit angestiegen ist,
diesen Satz in verschiedenen Kontexten anzuwenden. Auf der vertikalen Achse,
der Y-Achse, ist abgetragen, wie sich das Beweisverständnis verändert. Sie sehen,
hier gibt es eine ziemliche Streuung. Wir haben links unten eine Schulklasse,
die in beiderlei Hinsicht ziemlich schlecht abschneidet. Die Ursachen sind vielfältig:
Das ist z. B. eine Lerngruppe, die unter äußerst schwierigen Bedingungen in
einer Metropole mit hohem Migrationsanteil arbeitet. Die Streuung tritt auf,
obwohl es sich nur um Gymnasial- und Realschulklassen handelt, es ist keine
Hauptschulklasse dabei. Rechts oben haben wir ein Beispiel, bei dem es in exzellenter
Weise gelingt, in beiden Dimensionen sehr gute Leistungsfortschritte zu erbringen.
[1] Prenzel, M./Allolio-Näcke, L. (Hg.) (2006). Untersuchungen zur Bildungsqualität von Schule. Abschlussbericht des DFG-Schwerpunktprojekts. Münster: Waxmann.
