Zusammenhänge

Infobox

Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Bitte beachten Sie, dass der Bildungsplan fortgeschrieben wurde.

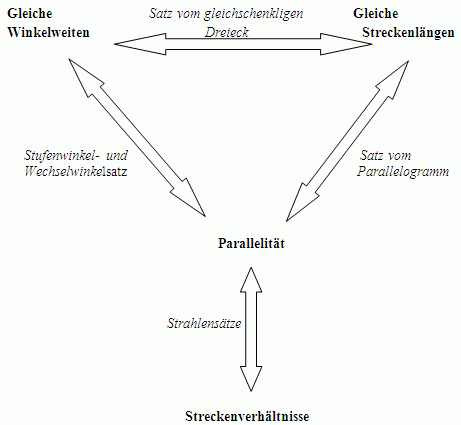
Überblick: Der Zusammenhang zu den grundlegenden geometrischen Aussagen über

- Gleiche Streckenlängen
- Gleiche Winkelweiten
- Parallelität
- Gleiche Streckenverhältnisse

Viele Aussagen der Geometrie lassen sich auf diese „Grundaussagen“ zurückführen.

Welche Sätze stellen einen Zusammenhang zwischen diesen Aussagen her?

Dies setzt sich in der analytischen Geometrie fort. Auch dort lässt sich das Beweisen nach den oben genannten Aussagen strukturieren und mit Verfahren nachweisen:

- Zeige Parallelität. Verfahren: Zeige, dass zwei Vektoren
Vielfache voneinander sind.

- Zeige gleiche Streckenlängen. Verfahren: Zeige, dass zwei Vektoren
gleich lang sind (bzw. identisch, falls sie parallel sind).

- Zeige ein Teilverhältnis. Verfahren: Streckenzug.

Dazu kommt: Zeige Orthogonalität. Verfahren: Zeige, dass das Skalarprodukt zweier Vektoren Null ist.

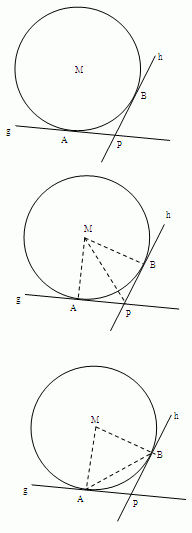
Beispiel zum Einsatz der Strategien
Zeige: AP = BP.

Strategische Überlegungen eines Schülers:
Welches Beweismittel kommt überhaupt in Frage?
Wie setze ich dieses Beweismittel ein?

1) Ich versuche kongruente Dreiecke zu finden, die jeweils eine der Seiten AP und BP enthalten.

Dazu muss ich Dreiecke einzeichnen.
Vermutung: Die Dreiecke APM und PBM sind kongruent.
Beweis: Ich verwende den KGS sws.
             Dreieck APM     Dreieck PBM
Seite s ₁            AM = Radius = BM
Winkel w      Rechter Winkel bei A bzw. B
Seite s ₂            PM        =            PM
Da die Dreiecke kongruent sind, stimmen Sie in allen entsprechenden Stücken überein, insbesondere in der dritten Seite.
Also AP = BP.

2) Ich versuche ein gleichschenkliges Dreieck zu finden, das die Schenkel AP und BP hat.
Vermutung: Das Dreieck APB gleichschenklig.
Beweis: Ich muss zeigen, dass die Basiswinkel bei A und B gleich weit sind.
Das geht so: AM = BM, also sind die Basiswinkel des Dreiecks ABM gleich weit, z.B. α (S.v.gleichsch.D. 1).
Dann sind die Basiswinkel des Dreiecks APB beide 90° - α, also gleich. Deshalb muss AP = BP sein (S.v.gleichsch.D. 2).

Strategische Überlegungen mit Zirkel und Lineal

Wenn die Schüler in die Lage versetzt werden, solche Beweise mit den vorgeschlagenen Hilfen selbst zu „erfinden“, werden sie oft auf verschiedene Lösungswege kommen. In diesem Fall von „methodenoffener“ Aufgabe sollte man die Unterrichtsmethode so wählen, dass verschiedene Wege auch gewinnbringend diskutiert werden können.

Logisch-deduktiv strukturieren – Eine kognitive Herausforderung:
Herunterladen [pdf] [358 KB]