Rolle der Kongruenzsätze
Infobox
Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Bitte beachten Sie, dass der Bildungsplan fortgeschrieben wurde.
Welche Rolle spielen die Kongruenzsätze für Dreiecke im Rahmen der Begründungssysteme ?
Warum wird überhaupt die Kongruenz von Figuren eingeführt?
Dazu ein wenig Theorie: Alle Begriffe und Sätze der Schulgeometrie bis Ende Kl. 7 wurden mit Hilfe der Abbildungen bzw. der Symmetrie entwickelt. Auch der weitere Aufbau der Kongruenzgeometrie könnte zunächst auf der Basis der Abbildungen und der daraus abgeleiteten Sätze geleistet werden. Dieses Vorgehen wäre aber ungeschickt, da es viele Beweissituationen gibt, bei denen das Beweisen mit Abbildungen oder der Begründungsbasis (II) sehr umständlich, hingegen das Beweisen mit Kongruenzsätzen relativ einfach ist.
Grob gesagt sind die Kongruenzsätze besonders nützlich, wenn wie im Beispiel von Seite 4 die Strecken und Winkel „weit voneinander entfernt“ sind.
Beispiele, bei denen das Beweismittel KGS ins Auge springt (Nr. 1 und 2).
|
1)
|
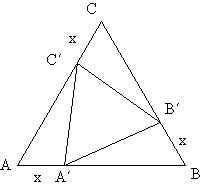
Das Dreieck ABC ist gleichseitig. Von den Ecken wird jeweils die gleiche Strecke x entgegen dem Uhrzeigersinn abgetragen. Zeige: Das Dreieck A´B´C` ist ebenfalls gleichseitig. Beweisidee: Die Dreiecke AA´C´, BB´A´ und CC´B` sind nach dem Kongruenzsatz sws kongruent. |
2)
|
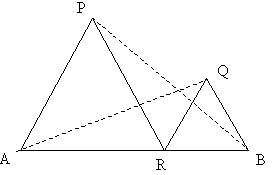
Es sind zwei gleichseitige Dreiecke wie in der Figur gegeben.
Zeige:
Beweisidee (1): Die Dreiecke ARQ und PRB sind nach dem KGS sws kongruent. Beweisidee (2): Die Drehung um R mit Drehwinkel 60° bildet B genau auf Q und P genau auf A ab. |
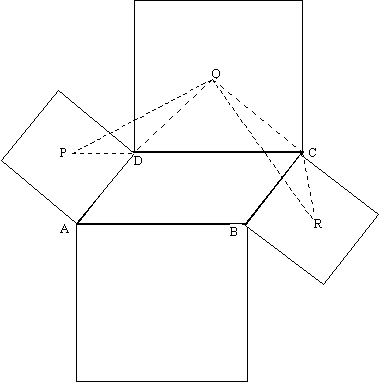
3) Satz von Napoleon: Errichtet man über jeder Seite eines Parallelogramms ein Quadrat, so bilden auch die Quadratmitten ein Quadrat.
Hier springen die KGS nicht ins Auge, weil schlichtweg keine Dreiecke da sind. Hier hilft das strukturierte Fragen (siehe S.23): Welche Möglichkeiten haben wir überhaupt, z.B. PQ = QR nach zu weisen? Vielleicht mit dem Satz von der Mittelsenkrechten? (Kann man irgendwo eine Mittelsenkrechte einzeichnen ?) Oder dem Satz vom gleichschenkligen Dreieck ? (Kann man irgendwo ein gleichschenkliges Dreieck einzeichnen?) Oder den Kongruenzsätzen ? (Kann man irgendwo Dreiecke einzeichnen, die vermutlich kongruent sind?)
Beweisidee: Die Dreiecke PDE und RCQ sind nach sws kongruent.
Die Kongruenzsätze sind mit der Begründungsbasis (I) beweisbar. Die Beweisbedürftigkeit ist allerdings schwer zu motivieren, weshalb in der Schule die Kongruenzsätze besser unmittelbar als aus der Anschauung gewonnene „Axiome“ zur bisherigen Begründungsbasis dazu genommen werden. Wichtig ist m.E. jedenfalls, die KGS auch tatsächlich als Beweismittel einzusetzen.
Zusammenfasssung: Das Beweisen wird wesentlich erleichtert, wenn man als Hilfsmittel die Kongruenzsätze für Dreiecke zur Verfügung hat. Übrigens sind in den Elementen von Euklid die Kongruenzsätze das zentrale Beweismittel.
Am Ende der Klasse 8 stehen somit als Beweismittel zur Verfügung:
- Die Begründungsbasis (I), die allerdings immer mehr in den Hintergrund rückt.
- Die Zusammenhänge (II) und die daraus bewiesenen Sätze.
- Die Kongruenzsätze für Dreiecke (III).
Kongruenzsätze für Dreiecke (III)
(sss) Wenn in zwei Dreiecken entsprechende Seiten gleich lang sind, dann stimmen sie in allen entsprechenden Stücken überein.
(sws) Wenn zwei Dreiecke in zwei Seiten und dem eingeschlossenen Winkel übereinstimmen, dann stimmen sie in allen entsprechenden Stücken überein.
(wsw und sww) Wenn zwei Dreiecke in einer Seite und zwei gleichliegenden Winkeln übereinstimmen, dann stimmen sie in allen entsprechenden Stücken überein.
(ssw) Wenn zwei Dreiecke in zwei Seiten und dem Gegenwinkel der größeren Seite übereinstimmen, dann stimmen sie in allen entsprechenden Stücken überein.
Logisch-deduktiv strukturieren – Eine kognitive Herausforderung:
Herunterladen
[pdf]
[358 KB]