Blick über den Tellerrand
Infobox
Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Bitte beachten Sie, dass der Bildungsplan fortgeschrieben wurde.
5. Ein Blick über den Tellerrand: „Akademische Anforderungen“ im holländischen Abitur
Die folgende Aufgabe zusammen mit den Informationen über das niederländische Abitur ist entnommen aus:
Offene und realitätsbezogene Aufgaben für den Mathematikunterricht, Anregungen aus der niederländischen Wiskunde, Hrsg. KuMi NRW; Klett-Verlag 2007
In der niederländischen Oberstufe gibt es die „Wiskunde A“ und die akademischere „Wiskunde B“. Seit 1999 ist in Wiskunde B die Euklidische Geometrie wieder im Lehrplan der Oberstufe und Thema im Abitur. Es sollen dadurch logisches Denken, korrektes Begründen und zielgerichtetes Problemlösen gefördert werden. Dabei werden als Beweismittel im Abitur lediglich die Grundlagen der Kongruenzgeometrie vorausgesetzt, wie sie bei uns bis zur achten Klasse gelehrt wird. Der Anspruch der Aufgaben liegt nicht in Bereich des Wissens oder von Verfahren , sondern im Auffinden eines mehrschrittigen Beweisweges und in der korrekten Begründung und Darstellung der einzelnen Beweisschritte.
(Man sieht: Relativ wenig Inhalt bei relativ viel Begründungs-Kompetenz und hohen kognitiven Anforderungen.) Entsprechend muss die Korrektur und die Bewertung der Aufgaben widerspiegeln, in wie weit die Begründungs-Kompetenz entwickelt ist.
Aufgabe: Auf einer Geraden (Examen 2002)
In Abbildung 1 sind zwei sich berührende Kreise c 1 und c 2 eingezeichnet mit den Mittelpunkten M 1 und M 2 . Der Berührpunkt der beiden Kreise ist S. Die Gerade l berührt den Kreis c 1 in P und den Kreis c 2 in Q. Die gemeinsame Tangente an c 1 und c 2 schneidet die Gerade l im Punkt T.
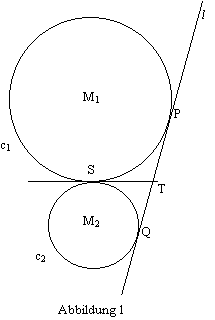
Frage 1 (5 Punkte)
Beweise, dass die Punkte P, Q und S auf einem Kreis liegen.
(Bem. von mir: Soll wohl „Beweise, dass die Punkte P,Q und S auf einem Kreis
um T liegen.“ heißen.)
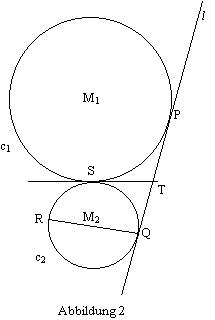
Außerdem ist der Durchmesser QR durch c 2 gegeben. Siehe hierzu die Abbildung 2.
Frage 2 (6 Punkte)
Beweise, dass die Punkte P, S und R auf einer Geraden liegen.
Lösung zur Aufgabe: Auf einer Geraden
|
Frage 1
|
Punkte |
|
|
●
|
2 |
|
|
● Daher ist
|
1 |
|
|
● Analog gilt
|
1 |
|
|
● Daher liegen P, Q und S auf einem Kreis mit Mittelpunkt T |
1 |
|
|
alternativ: |
||
|
●
|
1 |
|
|
● Daher ist das Dreieck M 1 PT kongruent mit Dreieck M 1 ST (Kongruenzsatz SSW g ) |
1 |
|
|
● Daher ist
|
1 |
|
|
● Analog gilt
|
1 |
|
|
● Also liegen P,Q und S auf einem Kreis mit dem Mittelpunkt T. |
1 |
PST =
SPT (Winkel
zwischen Sehne und Tangente)
(gleichschenkliges
Dreieck)
M
1
PT
=
TSM
1
= 90°;
;
(Bem. von mir: Es gibt noch einen weiteren Lösungsweg, der den Kehrsatz des S.v.Thales benützt.)
|
Frage 2 (max. 6 Punkte) |
Punkte |
|
|
●
|
2 |
|
|
●
|
2 |
|
|
●
|
1 |
|
|
● Daher liegen P, S und R auf einer Geraden. |
1 |
|
|
alternativ: |
||
|
● M
1
S und M
2
S
stehen beide senkrecht auf der gemeinsamen Tangente in S, daher liegt
S auf
|
1 |
|
|
● M 1 P und RQ stehen senkrecht zu l , daher ist M 1 P║RQ |
1 |
|
|
●
|
1 |
|
|
●
|
1 |
|
|
● Daher ist
|
1 |
|
|
● Daher liegen P, S und R auf einer Geraden, denn P und R liegen nicht auf derselben Seite von M 1 M 2 . |
1 |
PSQ = 90°
(Satz von Thales)
QSR = 90°
(Satz von Thales)
PSQ +
QSR = 180°
PM
1
M
2
=
RM
2
M
1
(Wechselwinkel)
PSM
1
= 0,5
.
(180° -
RM
2
M
1
)
und
RSM
2
= 0,5
.
(180° -
RM
2
M
1
)
PSM
1
=
RSM
2
Ein Beweis als Klassenarbeitsaufgabe ?
Wenn man Begründungskompetenz in einer Klassenarbeit prüfen möchte, ist m.E. sehr zu beachten: In Prüfungssituationen hat man selten Lichtblitze und Ideen, weshalb man solche auch nicht einfordern darf. Das ist auch gar nicht notwendig. Denn wir wollen ja keine „Lichtblitzkompetenz“ prüfen, sondern „Begründungskompetenz“. Der Schüler sollte also in der Lage sein, mit durchschnittlicher Kenntnis der Beweismittel die Beweisidee zu finden.
Bewerten kann man dann folgendes (wie in der Abitur-Aufgabe versucht):
- Ist das Beweismittel grundsätzlich richtig gewählt und verwendet?
- Sind für jeden Schritt stichhaltige Beweismittel angegeben?
- Ist die Abfolge der Beweisschritte stringent?
Logisch-deduktiv strukturieren – Eine kognitive Herausforderung:
Herunterladen
[pdf]
[358 KB]