Umkreis

2. Die Beweise zum Umkreis und Umkreismittelpunkt U.

Die Tatsachen zum Umkreis umfassen zwei verschiedene Aspekte, einmal den Sachverhalt zum folgenden Satz 1 und zum zweiten den Sachverhalt zum Satz 2.

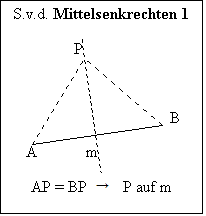
Satz 1: Wenn U der Schnittpunkt von zwei Mittelsenkrechten (der Seiten) in einem Dreieck ABC ist, dann hat U zu jeder Ecke des Dreiecks den gleichen Abstand.

Beweis:

U sei z.B. der Schnittpunkt von m _c und m _a .
Da U auf m _c liegt, ist AU = BU.  (a)
Da U auf m _a liegt, ist BU =  CU.  (a)
Aus AU = BU und BU = CU folgt: AU = BU = CU.

Benützte Sätze: Satz von der Mittelsenkrechten

(a) Liegt ein Punkt Q auf der Mittelsenkrechten von PP´, dann sind die Abstände PQ und P´Q gleich.

Aus Satz 1 folgt: Zu jedem Dreieck gibt es einen Kreis, der durch alle drei Ecken des Dreiecks geht. Sein Mittelpunkt ist U und sein Radius ist AU (= BU = CU).

Satz 2: In jedem Dreieck ABC schneiden sich alle drei Mittelsenkrechten (der Seiten) in einem gemeinsamen Punkt.

Beweis:
U sei z.B. der Schnittpunkt von m _c und m _a .
Da U auf m _c liegt, ist AU = BU.   (a)
Da U auf m _a liegt, ist BU =  CU.  (a)
Aus AU = BU und BU = CU folgt: AU =  CU.

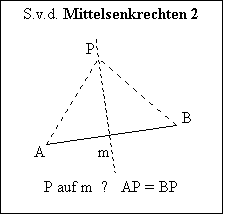
Aus AU = CU folgt: U liegt auf m _b .  (b)!

Benützte Sätze: Satz von der Mittelsenkrechten
a) Liegt ein Punkt Q auf der Mittelsenkrechten von PP´, dann sind die Abstände PQ und P´Q gleich  und  
b) Hat ein Punkt Q von P und von P´ denselben Abstand, dann liegt Q auf der Mittelsenkrechten von PP´.

Didaktische Bewertung:  Diese Beweise können gelingen, wenn u.a. für folgendes gesorgt ist:

• die Schüler sind schon überzeugt (praktische Übungen), dass es einen Punkt U mit demselben Abstand von den  Ecken gibt.
• Die Klasse wird auf einen Blickwechsel eingestimmt: Es geht jetzt um eine Herleitung aus bekannten Sachverhalten.
• Die Beweismittel sind der Klasse plakativ offen gelegt (z.B. zwei Plakate an der Wand mit treffender Kurzdarstellung der Sätze zur Mittelsenkrechten). Z.B. so:

Wir müssen nachweisen, dass die Strecken AU, BU und CU gleich lang sind. Die Plakate zeigen die Sätze (die Begründungen), die wir in der Geometrie bisher benützen können.
Welche  Sätze könnten zur Lösung des Problems beitragen ?

Neben den Plakaten von S.20 müssen vorhanden sein:

	Evtl. auch:
	S.v.d.  Winkelhalbierenden 2    x = y  →  P auf WH		S.v.d.  Winkelhalbierenden 1 P auf WH  → x = y

 

 

 

Logisch-deduktiv strukturieren – Eine kognitive Herausforderung:
Herunterladen [pdf] [358 KB]