Winkelsumme Viereck

4. Exkurs zur Winkelsumme im Viereck

Wenn man schon einmal bei der Winkelsumme ist, wird traditionell anschließend die Winkelsumme im Viereck bewiesen. Als Beweismethode wird die Aufteilung in zwei Dreiecke verswendet. Dieses Vorgehen ist m.E. an dieser Stelle problematisch: Der Beweis der Winkelsumme im Dreieck ist oft der erste richtige Beweis im Leben eines Schülers in dem Sinne, dass das Vorgehen lückenlos mit früheren Sätzen begründet wird. Insbesondere hat er den Erfolg gesehen, den ein strategischer Blick bzw. eine Analyse der früheren Sätze hinsichtlich der Beweisidee „zeichne eine Hilfsparallele“ hat.  

Und jetzt kommt der zweite Beweis im Leben eines Schülers mit einer ganz neuen Beweisidee! Wobei es doch auch mit Parallelen geht:

Beweis der Winkelsumme im Viereck mit der Parallelenmethode

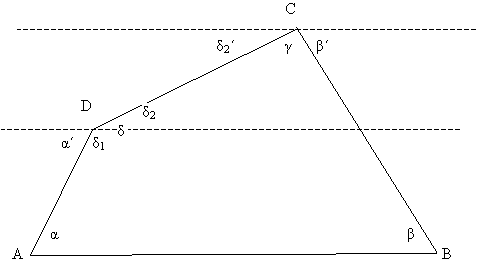
δ wird in δ ₁ und δ ₂ aufgeteilt;

δ ₂ = δ ₂ ´  und  α = α´ und β = β´ (Wechselwinkel an Parallelen)

Ecke C:  δ ₂ + γ + β = 180°

Ecke D:  α +δ ₁        = 180°     

α + β + γ + δ           = 360°

Diese Methode kann theoretisch auch bei Fünfecken, Sechsecken usw. angewendet werden. Was aber nicht gelingt, ist ein allgemeiner Beweis für die Winkelsumme im n-Eck. Dieser mit müsste mit vollständiger Induktion geführt werden,  wobei im Induktionsschritt ein Dreieck dazu genommen wird. Erst hier, wenn man einen Satz über die Winkelsumme im n-Eck beweisen will, ist also die Zerlegung in Dreiecke notwendig.

Im Sinne einer Kompetenzentwicklung ist also nicht das primäre Ziel, Inhalte zu erschließen (im Sinne von: Wichtig ist, dass die Schüler die Winkelsumme im Viereck kennen), sondern die deduktiven Fähigkeiten des Schülers weiter zu entwickeln. Natürlich ist auch die Zerlegung in Dreiecke ein wichtiges Beweis- und Problemlöseprinzip und man sollte es auch bringen. Nur nicht gleich bei der Winkelsumme im Viereck.

Logisch-deduktiv strukturieren – Eine kognitive Herausforderung:
Herunterladen [pdf] [358 KB]