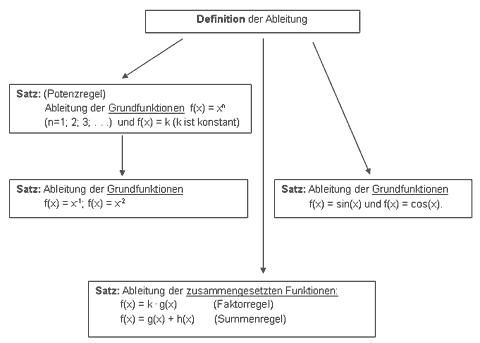
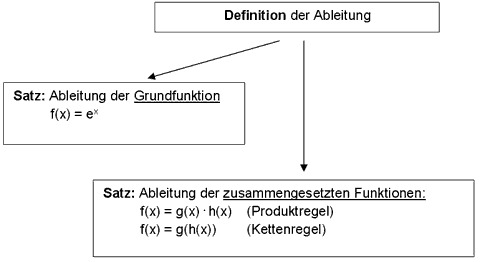
Ketten- und Produktregel

Von der Sachlogik her sind verschiedene Reihenfolgen Produktregel – Kettenregel beziehungsweise Kettenregel – Produktregel möglich.
Hier wird die Reihenfolge Kettenregel – Produktregel vorgezogen; wegen der Abhängigkeit von der Reihenfolge ist damit im Schülermaterial zu beachten, dass das Arbeitsblatt zur Produktregel die Kenntnis der Kettenregel voraussetzt.

Bei der Kettenregel und der Produktrege l sind die Hauptprobleme:

1. Wie kommt man überhaupt auf die Regel?
2. Die Beweise sind sehr formal, haben einen hohen algebraischen Anspruch und benötigen die Vertrautheit mit der Definition der Ableitung, die schon ein Jahr zurückliegt.
3. Ein formaler Beweis, ohne dass vorher die Aussage der Regel einsichtig gemacht wurde, kann nur frustrierend sein.

Bei beiden Regeln wird der Schwerpunkt auf die Technik der Heuristik gelegt. Wie kommt man auf eine Vermutung ?  Wie wird die zu beweisende Aussage einsichtig?
Man weiß ja zunächst gar nicht, was man beweisen soll. Das ist ein Punkt, auf den noch zu wenig geachtet wurde. Diese Problematik ist jetzt im Zusammenhang der Ableitungsregeln ganz neu und eine Gelegenheit, mit heuristischen Methoden (Bildungsplan: überfachliche Kompetenzbereiche) zu arbeiten.
( Heuristik ( altgr. Heurísko; ich finde; heuriskein ; (auf-)finden, entdecken) bezeichnet die Kunst, mit begrenztem Wissen und wenig Zeit zu guten Lösungen zu kommen.)

Natürlich ist es auch möglich die entsprechenden Vermutungen zur Regel aus einer anwendungsbezogenen Situation herzuleiten. An dieser Stelle wird aber innermathematisch gearbeitet, um eine möglichst eigenständige Schülertätigkeit mit dem Fokus auf das Aufstellen der Vermutung zu richten.

Zur Produktrege l noch genauere Ausführungen und eine Diskussion von Alternativen:
Der Schüler denkt: Ist doch klar, dass (f·g)´= f´·g´ gilt. Das muss im Untericht zuerst thematisiert werden; hier handelt es sich auch um eine wichtige Denktechnik. Dazu braucht man zwei Funktionen, die man einzeln und als Produkt ableiten kann (z.B. x ² und x ³ ; oder man nimmt den GTR).

Heuristischen Methoden sind unter anderem:

1. geeignete Beispiele
2. Veranschaulichung
3. gezielte Suche: Gab es schon mal ähnliches?

Diese heuristischen Zugänge zur Produktregel sollen nun vergleichen werden.

1. geeignete Beispiele.

Man füllt eine Tabelle der Art aus.

Vorteile: Falls die Schüler darauf kommen, haben Sie ein gutes Gefühl (Problem gelöst). Man kann daran erläutern, was zielgerichtete Beispiele sind (mache von den zwei Größen eine einfach, variiere zunächst nur eine Größe).

Nachteile: Nicht alle Schüler kommen auf Ideen, insbesondere ist nicht von allen Sch zu erwarten, dass sowohl Funktionen als auch deren Ableitungen in symmetrischer Anordnung in der Regel wiederzufinden sind/sein müssen. Es ist auch möglich dieses Phänomen im Nachgang zu beleuchten.

Ist die richtige Vermutung gefunden, so steht erneut die Frage im Raum welchen Sinn ein Beweis noch haben kann, wenn die Regel gefunden offensichtlich gefunden ist? Ferner sieht man nicht, warum sich gerade diese Regel ergibt. Ein geeigneter Unterrichtsgang (Aufstellen der Vermutung, Einsichtigmachen eines Beweises) kann versuchen vermeintliche Nachteile ins Gegenteil zu kehren.

2. Veranschaulichung.

In vielen Büchern wird mit einem Rechteck als Veranschaulichung gearbeitet.

Will man die Ableitung eines Produkts f = u · v zweier Funktionen u und v bestimmen, deren Ableitung man kennt, so muss man den Differenzenquotienten von f auf die Differenzenquotienten von u und v zurückführen. Es ist

Deutet man die beiden Produkte im Zähler   u(x ⁰ +h) · v(x ⁰ +h) und u(x ⁰ ) · v(x ⁰ )) als Flächeninhalte von Rechtecken mit den Seitenlängen u(x ⁰ +h) usw., so erhält man eine Idee für eine mögliche Umformung der Differenz u(x ⁰ +h) · v(x ⁰ +h)  -  u(x ⁰ ) · v(x ⁰ ).

Subtraktion der beiden Rechteckflächen liefert:

Diese Umformung ist nicht nur anschaulich, sondern auch rechnerisch richtig, da lediglich das Produkt  u(x ⁰ +h) · v(x ⁰ ) addiert und anschließend wieder
subtrahiert wird.
Für den Differenzenquotient (*) gilt damit:

Vorteile: Die zentrale Idee „Zurückführung auf die zwei anderen Differenzenquotienten“ kommt gut heraus; der Beweis wird gleich mitgeliefert. Man kann die Umformungen anschaulich begleiten.
Nachteile: Die Zurückführung auf die Definition ist rechenaufwändig, viele Variablen.
Es wird eine Veranschaulichung „Rechteck“ gebracht, die noch nie da war; auch dazu kann es Schülerfragen geben.

3. Gezielte Suche: Gab es schon mal so etwas?

Gesucht: (fg)´, also die Ableitung eines Produktes von Funktionen.
Frage: Kommt ein solches Produkt in einem anderen Zusammenhang vor, den wir nützen können?  (Die Idee mit der binomischen Formel muss man natürlich vorgeben.)

Vorteile: Kein Vorwissen zur Definition der Ableitung notwendig; Vermutung und Beweis in einem Gang.
Nachteile: Hoher abstrakter Anspruch;  eventuell geht es zu schnell, zu wenig Zeit zum Vertraut-Werden mit der Problematik. Sieht ein wenig wie ein Trick aus. Auf dem Arbeitsblatt 14 ist die gezielte Suche dahingehend umgesetzt, dass parallel zu den einzelnen Beweisschritten zielführende Verständnisfragen den Beweis begleiten.

Arbeitsblatt 12  Einführung der Verkettung von Funktionen (für alle Schüler)
Arbeitsblatt 13   Ableitung einer Verkettung (für alle Schüler)
Arbeitsblatt 14   Ableitung eines Produktes (für alle Schüler; Aufg.3 anspruchsvoll)