Näherungsformel von Moivre-Laplace
Infobox
Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Bitte beachten Sie, dass der Bildungsplan fortgeschrieben wurde.
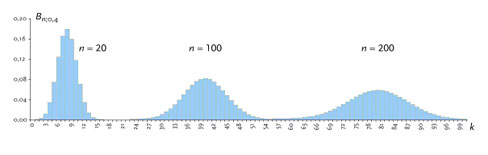
Betrachtet man die Binomialverteilungen
für wachsendes n bei konstantem p, so werden die Histogramme einer binomialverteilten Zufallsvariablen breiter und symmetrischer um den Erwartungswert
.
Die Wahrscheinlichkeit eines einzelnen Ergebnisses wird immer kleiner, da die Flächensumme der Rechtecke immer die Gesamtwahrscheinlichkeit 1 ergibt.
Die Histogramme erhalten zunehmend Glockenform, wobei sich die (Symmetrie-)Achse an der Stelle
immer mehr nach rechts verschiebt.
Um das Verhalten von
für große Werte von n besser untersuchen zu können, verschiebt man die Schaubilder so, dass der Erwartungswert
auf der 2. Koordinatenachse liegt und gleicht somit die Verschiebung der (Symmetrie-) Achse aus. Jeder Wert X=k wird um
Einheiten nach links verschoben.
Gleichzeitig streckt man die Rechteckshöhen, die
, mit dem Faktor
und die ursprünglichen Rechtecksbreiten mit 1LE mit dem Faktor
. Damit gleicht man das Flacherwerden der Glockenform aus und hat gleichzeitig die Konstanz der Flächenmaßzahlen der Rechtecke (der Einzelwahrscheinlichkeiten) gewahrt.
Damit gilt:
Man erhält eine neu Zufallsvariable, ein
standardisierte Zufallsvariable
.
Für
nimmt die standardisierte Zufallsvariable positive, für
negative Werte an.
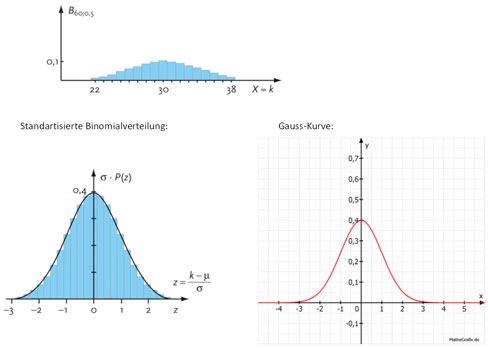
Eine solche Verteilung heißt
standardisierte Binomialverteilung
:
De Moivre hat erkannt, dass die Histogramme bestimmter standardisierter Binomialverteilungen trotz unterschiedlicher Parameter n und p in guter Näherung einen fast identischen Verlauf zeigen. Diese Histogramme haben einen glockenförmigen Verlauf.
Laplace hat diese Überlegungen weitergeführt und erkannt, dass die Histogramme standardisierter Binomialverteilungen um so besser von glockenförmigen Graphen umrandet werden, je größer die Standardabweichung
ist.( Faustregel: Wenn die Laplace-Bedingung
erfüllt ist)
Das Schaubild der Funktion
liefert die „Grenzkurve“ ,die Glockenkurve (als Grenzlage der Histogramme für
)
Diese Funktion
heißt
Gauß-Funktion
, ihr Schaubild heißt
Gauß’sche Glockenkurve.
Diese Glockenkurve ist symmetrisch zur y-Achse und hat die x-Achse als Asymptote.
Moivre hat diese Glockenkurve für p=0,5 untersucht, Laplace zeigte, dass sich auch im Fall
für große Werte von n dieselbe Grenzkurve ergibt.
Beispiel: Binomialverteilung mit n=60, p=0,5,
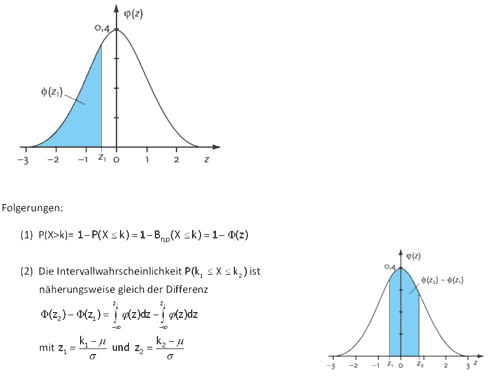
Der Flächeninhalt zwischen der Gauß-Kurve und der x-Achse entspricht somit dem der Summe der Inhalte aller Rechtecksflächen des Histogramms einer binomialverteilten Zufallsvariablen X ebenso wie die der dazugehörigen standardisierten Zufallsvariablen Z und hat der Wert 1:
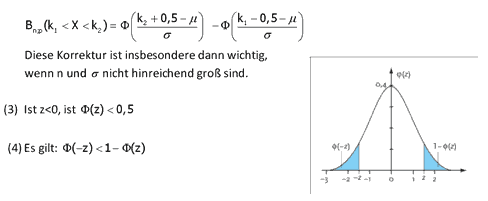
Die Summenwahrscheinlichkeit
kann dann näherungsweise durch den Inhalt der Teilfläche, die von der Gauss-Kurve und der x-Achse (bzw. z-Achse) im Intervall
eingeschlossen wird, berechnet werden:
