Lokale Extremstellen
Infobox
Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Bitte beachten Sie, dass der Bildungsplan fortgeschrieben wurde.
Didaktische Bemerkungen
1) In der Definition tritt zum ersten Mal der Begriff „Umgebung“ auf. Diesen neuen Begriff kann man vermeiden, wenn man einfach den bekannten Begriff „Intervall“ verwendet (ob offen oder geschlossen ist einerlei). Also:
|
Eine Stelle x
0
heißt Extremstelle und f(x
0
) Extremwert von f (genauer: lokales Extremum),
wenn es eine Intervall I gibt mit x 0 ∈I und f(x) £ f(x 0 ) für alle x ∈I (f(x 0 ) ist lokales Maximum) |
2) Man fragt sich, warum man bei einem Minimum nicht f(x) > f(x 0 ) statt f(x) ≥ f(x 0 ) verlangt. Das „echt größer“ würde doch der Grundvorstellung von Minimum näher kommen. Hatte man da vielleicht so etwas wie die nebenstehende Funktion im Auge? Die Funktion f mit

hat anschaulich bei x 0 = 0 eine Minimumstelle und sie nimmt in jeder Umgebung der Stelle x 0 = 0 den Wert 0 an.

3) Die Definition der Ableitung bezieht sich auf beliebige Funktionen, die Kriterien sind dagegen nur noch bei differenzierbaren Funktionen anwendbar. Das hat zur Folge, dass die Grundvorstellung der Schüler zum Begriff „lokale Extremstelle“ ausschließlich den Fall A in den nachfolgenden Beispielen umfasst. Es ist m.E. nicht begründbar, wenn man im Unterricht eine formale Definition bringt, sie aber letztlich an keiner Stelle benützt, sondern lediglich mit der Anschauung Fall A arbeitet. Andererseits sollte der Lehrer klar herausstellen, dass die Kriterien lediglich Extremstellen bei differenzierbaren Funktionen behandeln.
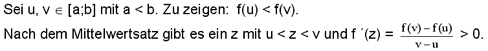
Zu den Arbeitsblättern:
Arbeitsblatt 17
Definition von „Lokale Extremstelle“ (für alle Schüler; Aufg. 3 für gute Schüler)
