Das Taxiproblem

Infobox

Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Bitte beachten Sie, dass der Bildungsplan fortgeschrieben wurde.

(nach Arthur Engel)

Taxi

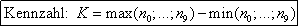
Die Taxen in Frankfurt sind nummeriert: 1; 2; 3; … .
Nach Auskunft des Taxifahrers gibt es in Frankfurt 3000 Taxen.
Danach beobachte ich 4 Taxen mit den Nummern 512; 987; 355; 1200.

Annahme : Der Taxifahrer hat recht.
Die Wahrscheinlichkeit, ein Taxi mit einer Nummer kleiner oder gleich 1200 anzutreffen, beträgt dann .
Die Wahrscheinlichkeit, 4 solche Taxen anzutreffen, beträgt .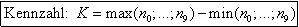
Entscheidung : Dieser Zahlenwert ist ein Indiz gegen die Annahme.
Ich lehne die Aussage des Taxifahrers ab.
Aber : Mit einer Wahrscheinlichkeit von 2,6 % habe ich zufällig 4 Taxen
mit einer Nummer kleiner oder gleich 1200 unter den 3000 erwischt.
Dann hat der Taxifahrer doch recht.
Meine Irrtumswahrscheinlichkeit beträgt 2,6 %.

Testen von Hypothesen

Die beiden Beispiele spiegeln die Grundkonstruktion eines Hypothesentests wider.
- Hier: Durchführung eines Tests auf der Stufe des inhaltlichen Argumentierens
Die Grundfrage beim Testen von Hypothesen lautet:
Ist das Stichprobenergebnis verträglich mit dem zu erwartenden Ergebnis oder weicht das Ergebnis signifikant ab? (vgl. Schema)

(Statistische Signifikanz: In der Statistik heißen Unterschiede oder Zusammenhänge signifikant, wenn die Wahrscheinlichkeit gering ist, dass sie durch Zufall zustande gekommen sind.)

Vorgehensweise im Schema:

Aufgrund des Stichprobenergebnisses kann also die Aussage über die Grundgesamtheit als unwahrscheinlich abgelehnt werden.
Es ist aber andererseits prinzipiell nicht möglich, allein unter Verwendung eines Stichprobenergebnisses eine Aussage über die Grundgesamtheit zu „beweisen“.