Das Projekt

Das Projekt: „Cola-Geschmackstest“

1. und 2. Stunde

Das Experiment
Wir wollen feststellen: Ist die Klasse eine Cola-Schmecker-Klasse oder nicht?
Der bevorstehende Test wird ausführlich erläutert:
In vier Gläser wird zufällig jeweils eine der Cola-Sorten Coca-Cola, Coca-Cola light und Pepsi Cola gefüllt. Man kann die Cola-Sorten z. B. durch viermaliges Werfen eines Würfels (1,2: Coca-Cola; 3,4: Coca-Cola light und 5,6: Pepsi Cola) auf die vier Gläser verteilen.
Mögliche Verteilungen werden ausführlich besprochen.
Die Aufgabe der Schüler besteht darin, nach dem Probieren aus den vier Gläsern jedem die richtige Cola-Sorte zuzuordnen und auf einem vorbereiteten Testbogen einzutragen (kein Vergleichstest!).
Wichtig: Kommentare beim Experiment beachten und später in Gespräch einbringen (keine Ahnung ... Raten ...)
Die 26 (je nach Klassengröße) ausgefüllten, noch nicht ausgewerteten Testbögen werden in einem verschlossenen Umschlag bis zur Auswertung am Ende des Projekts aufbewahrt (Motivation, emotionale Bindung).

Gruppenarbeit und Hausaufgabe:
Wie wollen wir auswerten?

In dieser Phase soll den Schülerinnen und Schülern die Möglichkeit gegeben werden, die entscheidende Idee „Betrachtung einer „Nix-Schmecker-Klasse“ zu finden.
Man könnte natürlich im Verlauf der Stunde einzelnen Gruppen helfen, muss es aber nicht.
(Wie können wir feststellen, ob wir gute Schmecker sind?
Was wäre die Alternative?
Könnten unsere Ergebnisse nicht auch durch Raten ganz zufällig entstanden sein?
Wo hört Raten auf, wo fängt schmecken an? …)

Die verschiedenen Vorschläge zum weiteren Vorgehen werden im Plenum diskutiert.
Sollte bisher eine „Nix-Schmecker-Gruppe“ als Vergleichsmöglichkeit nicht berücksichtigt worden sein, wird dies jetzt von der Lehrkraft angeregt.

Ergebnis:
Die Klasse vergleicht mit einer „Nix-Schmecker-Gruppe“ und einigt sich auf einen „Schmeckerbereich“.

Schätzen der Gesamtanzahl der Treffer bei „Schmeckern“ und „Nix-Schmeckern“ auf vorbereitetem Arbeitsblatt.

3. Stunde

• Simulation einer Klasse von 28 Nix-Schmeckern.
  Gespräch über Festlegung des Vorgehens:
• Zunächst Verteilung der Colasorten auf die Gläser durch Würfeln festlegen.
  Danach 28 × 4 mal würfeln, um den Geschmackstest zu simulieren (GTR).
• Ergebnisse der 14 (je zwei Schüler führen eine Simulation durch) Simulationen sammeln, mit Schätzwerten vergleichen und diskutieren.
  Wichtig: Sammeln eigener Erfahrungen über Zufallsschwankungen. Vergleich mit eigenen Erwartungen: Es kann sein, dass „Nix-Schmecker“ vergleichsweise gut abschneiden (Vorbereiten des Begriffs der Irrtumswahrscheinlichkeit).

4. Stunde

• Arbeitsauftrag
  Ermittle die Einzelwahrscheinlichkeiten für 0, 1,....,4 Treffer.
  

Es ist sinnvoll, die Anzahl der Proben auf 4 zu reduzieren, um eine Berechnung der Einzelwahrscheinlichkeiten mithilfe der Pfadregel zu ermöglichen, so dass die aus vorhergehenden Bausteinen bekannten Möglichkeiten des Baumdiagramms genutzt werden können.

Übung / Hausaufgabe
Variation der Trefferwahrscheinlichkeit
Variation der Probenanzahl (2, 3, 5)

5. und 6. Stunde

• Besprechung der Hausaufgabe unter Berücksichtigung der Aspekte:

  • Systematisches Abzählen und Überlegen
  • Baumdiagramm, Pfadregeln
  • Ausnutzen von Symmetrien
  • Überprüfen der Ergebnisse (z. B. geeignete Summenbildung)
• Verallgemeinerung für n Proben, Formel der Binomialverteilung:

Das Abzählergebnis kann mithilfe des Pascalschen Dreiecks verdeutlicht werden:

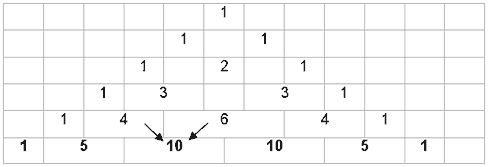
Um bei 5 Versuchen zwei Treffer zu erhalten, gibt es zwei Möglichkeiten: Man hat bei 4 Versuchen einen Treffer und dann einen weiteren Treffer oder man hat bei 4 Versuchen bereits zwei Treffer und dann eine Niete. Auf diese Weise kann das rekursive Vorgehen am Pascalschen Dreieck erarbeitet und verdeutlicht werden. Die Schritte von 5 nach 6, 6 nach 7, ......, usw.  werden nicht mehr einzeln durchgeführt, sondern die Berechnung der Wahrscheinlichkeiten erfolgt über die nun „gefundene Formel“  für die  Wahrscheinlichkeiten  und wird dann dem GTR überlassen.

 wird verwendet als Kurzschreibweise für die Anzahl der Pfade im Baumdiagramm, die bei n Proben zu k Treffern führen. Es wird darauf verzichtet den Term exakt über Fakultäten zu definieren.

• Übungs- und Hausaufgaben zu Binomialverteilungen
• Einsatz des GTR
  • Befehle „pdfbin“, „cdfbin“
  • grafische Darstellung (Histogramm)

7. bis 9. Stunde

Aufbau eines Hypothesentests:
Frage: Ist die Klasse eine „Cola-Schmecker-Klasse“?
Die Hypothese „ Die Klasse besteht aus Nix-Schmeckern“ soll widerlegt werden (Nullhypothese, Alternativhypothese).
Was leistet eine Nix-Schmecker-Gruppe?
Testvariable X (: Anzahl der „Treffer“ ) ist binomialverteilt mit n = 112 (28 mal 4) und p = .

.

Berechnung einzelner Wahrscheinlichkeiten mit dem GTR.
Wie groß ist die Wahrscheinlichkeit, dass eine „Nix-Schmecker-Klasse“ in dem in der 2. Stunde vereinbarten „Schmeckerbereich“ liegt?

Festlegen eines „neuen Schmeckerbereiches" (Entscheidungsregel).
Diskussion: Der „Schmeckerbereich“ (Ablehnungsbereich) kann nicht berechnet werden, sondern muss in einer „willkürlichen“ Entscheidung festgelegt werden.

Gespräch über die Unsicherheiten:
Je kleiner die Grenze, desto unsicherer eine mögliche Entscheidung zugunsten der Schmecker-Hypothese.
Maß für die Unsicherheit? Irrtumswahrscheinlichkeit. 
Berechnung der Irrtumswahrscheinlichkeit.

Interpretation der Irrtumswahrscheinlichkeit

Auswertung des Experimentes:
Der verschlossene Umschlag wird geöffnet, die Testbögen werden ausgewertet.
Wie viele Treffer hat die Klasse erzielt?
Kann die Nullhypothese abgelehnt werden?
Diskussion der Ergebnisse

Diskussion:
Mit welcher Wahrscheinlichkeit wird eine „Nixschmecker-Klasse“ fälschlicherweise als „Schmecker-Klasse“ eingestuft?
Die Trefferwahrscheinlichkeit für eine „Schmecker-Klasse“ ist eine willkürliche Festlegung.

Arbeitsblatt:
Mit welcher Wahrscheinlichkeit wird eine „Nixschmecker-Klasse“ fälschlicherweise als „Schmecker-Klasse“ eingestuft?
Berechnung für mehrere Trefferwahrscheinlichkeiten
Grafische Darstellung
Berechnung von Irrtumswahrscheinlichkeiten bei vorgegebenem Ablehnungsbereich.
Berechnung von Ablehnungsbereichen bei vorgegebenen Irrtumswahrscheinlichkeiten.

Stundenentwurf: Herunterladen [doc] [197 KB]

Stundenentwurf: Herunterladen [pdf] [44 KB]