Binärsystem
Die Schülerinnen und Schüler kennen unter Umständen schon das Binärsystem aus dem Mathematikunterricht, da in den Standards 6 neben dem Dezimalsystem ein weiteres Zahlsystem Inhalt ist.
Hier lernen sie einen neues Aspekt kennen: der Computer codiert alle Daten digital mit einer Folge von Nullen und Einsen, da es technisch am einfachsten realisierbar ist.
Beim Einstieg ins Binärsystem geht es zunächst einmal um die besondere Darstellung dieser Zahlen. Mit den Kärtchen, die die Schülerinnen und Schüler bekommen, können die Zahlen 0 bis 31 dargestellt werden. Wenn sie gleich von Beginn an für eine aufgedeckte Karte eine Eins und für eine verdeckte Karte eine Null schreiben, gewöhnen sie sich an die richtige Schreibweise.
Nach dem Kennenlernen der Binärzahlen mit ihrer besonderen Schreibweise lernen die Schülerinnen und Schüler, einfache Binärzahlen in Dezimalzahlen und umgekehrt umzuwandeln.
Dabei wird hier in der 7. Klasse ein einfacher Algorithmus zur Umwandlung gewählt.
Ist eine Binärzahl gegeben, werden die Zweierpotenzen addiert, an deren Stelle eine Eins steht.
Ist eine Zahl im Dezimalsystem gegeben, sucht man die größte Zweierpotenz, die in die Zahl passt, schreibt diese mit eins multipliziert als ersten Summanden auf (z.B. 1*64) und berechnet dann den Rest, bei dem man wieder nach der größten Zweierpotenz sucht, die in diesen passt. Dabei werden fehlende Zweierpotenzen mit null multipliziert aufgeschrieben.
Beispiel: Die Zahl 314 soll vom Dezimalsystem ins Binärsystem umgewandelt
- Schritt 1: Suche nach der größten Zweierpotenz, die in die Zahl passt: 256 (Schreibe:
1*256) - Schritt 2: Berechne den Rest: 314 – 256 = 58
- Schritt 3: Suche nach der größten Zweierpotenz, die in 58 passt: 32 (128 und 64 passen nicht, also wird geschrieben:
+0*128 + 0*64 + 1*32) - Schritt 4: Berechne den Rest: 58 – 32 = 26
- Schritt 5: Größte Zweierpotenz: 16 (Schreibe:
+ 1*16) - Schritt 6: Berechne den Rest: 26 – 16 = 10
- Der Rest ist klar und ist auch von den Schülerinnen und Schülern schon sehbar. Insgesamt erhält man:
314 = 1*256 + 0*128 + 0*64 + 1*32 + 1*16 + 1*8 + 0*4 + 1*2 + 0*1 + 1*2 + 0*1
Die Einsen und Nullen werden für die Binärschreibweise übernommen: 1 0 0 1 1 1 0 1 0 b
Andere Vorgehensweisen, wie z.B. die wiederholte Division durch 2 und das Betrachten des Restes, sind als MINT-Vertiefung möglich.
Anders als auf dem Tafelbild (s.u.) wird folgende Schreibweise favorisiert:
Ein „b“ direkt hinter der Zahl gibt an, dass die Zahl in Binärschreibweise vorliegt, ein „d“ kennzeichnet Dezimalschreibweise und später (nicht Inhalt in Klasse 7) ein „h“ die Hexadezimalschreibweise.
Beispiel: 1 1 0 d = 1 1 0 1 1 1 0 b
Addition, Subtraktion, Multiplikation und Division von Binärzahlen ist nicht Standardniveau in der 7. Klasse, kann aber durchaus als MINT-Vertiefung für interessierte Schülerinnen und Schüler genutzt werden. Wichtig ist hier, dass diese sich einfache Zahlen wählen und bei der Division auf Teilbarkeit achten.
Alle Rechenverfahren funktionieren natürlich auch im Binärsystem. Zum Teil sind sie sogar einfacher realisierbar, wie bei der Multiplikation, da nur die Multiplikation mit 0 oder 1 gebraucht wird. Die einzige Schwierigkeit, die aber nicht zu unterschätzen ist, stellt der ungewohnte Übertrag bei der Addition bzw. Subtraktion dar.

Mögliches Tafelbild
Binärsystem mit dem WTR
CASIO fx-87DE X:
Im Menü wählt man 2: Basis-N aus:
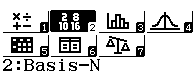
Im linken oberen Eck des Bildschirms wird das Zahlsystem angegeben, das ausschlaggebend für das Ergebnis einer Umwandlung oder Rechnung ist.
Ausgewählt wird es über die folgenden Tasten:

Um für die eingegebenen Zahlen das Zahlsystem anzugeben, wählt man OPTN und geht mit der Pfeiltaste nach unten.

1 : d steht für Dezimalschreibweise,
2 : h für Hexadezimalschreibweise,
3 : b für Binärschreibweise und
4 : o für Oktalschreibweise.
Beispiel:
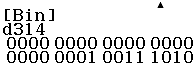
TI – 30 X Pro Multiview:
1. Umwandlung vom Dezimalsystem ins Binärsystem
eine Dezimalzahl eingeben
z.B. 100d
2nd 9 drücken,
toBin hervorheben
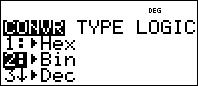
Enter drücken.
Ergebnis 1100100b
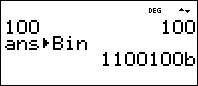
2. Umstellung des TI auf ein anderes Zahlsystem
Taste Mode drücken:
leider werden die Zahlsysteme nicht angezeigt

nach unten Scrollen und bin auswählen
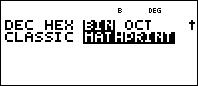
im Standardfenster können nun Rechenoperationen durchgeführt werden
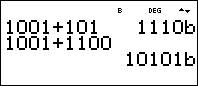
3. Umwandlung vom Binärsystem ins Dezimalsystem
im Binärmodus eine Binärzahl eingeben, z.B. 110011b

2nd 9 drücken (base n)
toDec hervorheben
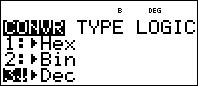
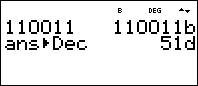
Enter drücken,
Ergebnis: 51d
Hintergrund zum Unterrichtsgang: Herunterladen [odt][562 KB]
Hintergrund zum Unterrichtsgang: Herunterladen [pdf][305 KB]
Weiter zu Textcodierung
