Symmetrische Chiffren
Klassische Chiffren heißen →symmetrisch, weil Absender und Empfänger den gleichen Schlüssel haben, mit dem die Nachricht ver- und entschlüsselt wird. Sie verfügen also über ein gemeinsames Geheimnis. Obwohl →asymmetrische Kryptosysteme oft „moderne“ Kryptoverfahren genannt werden, weil sie erst im 20. Jahrhundert aufkamen und ganz neue Möglichkeiten bieten, sind die symmetrischen Chiffren nach wie vor unverzichtbar. Bei Schülern entsteht oft die Fehlvorstellung, asymmetrische Verfahren seien irgendwie „besser“, weil sie neuer sind; tatsächlich eröffnen sie nur andere Einsatzgebiete. Ein Beispiel hierfür ist →SSL/TLS, das sowohl auf starke symmetrische als auch asymmetrische Chiffren angewiesen ist.
Didaktisch-methodische Hinweise
Die Auswahl der hier vorgestellten symmetrischen Chiffren ist unvollständig. Die Caesar-Chiffre bietet als Einstieg aber den Vorteil, dass fundamentale Begriffe und Vorgänge (Nachricht, →Klartext, →Chiffretext, →Chiffre, →Schlüssel, →chiffrieren/dechiffrieren, →brechen, →Angriff) an einem sehr einfachen Beispiel erläutert werden können. In der hier vorgeschlagenen Reihenfolge werden die Chiffren nacheinander gebrochen und die jeweils entscheidende Schwachstelle dann in der nächsten Chiffre geschlossen, was einen gut sichtbaren roten Faden durch die Einheit ergibt. Auch in der Geschichte der Kryptografie bewegt man sich damit allmählich voran. Dabei können aus Zeitgründen nicht alle Verfahren in Klasse 7 besprochen werden. Die Klasse 7 kann nur einen ersten Einblick in die Kryptologie gewähren.
Anfangs sind bei den Schülern insbesondere die Begriffe Chiffre, Schlüssel, ver-/entschlüsseln (de-/chiffrieren) und brechen noch sehr unscharf. Eine präzise Fachsprache erleichtert hier die Konzeptbildung (s. Glossar). Auch den Begriff →Codierung sollte man zunächst vermeiden, weil er sonst mit verschlüsseln verwechselt wird.
Es bietet sich an, die hier vorgestellten klassischen symmetrischen Chiffren alle nach dem gleichen Muster zu behandeln:
- Wie wird verschlüsselt?
- Wie wird entschlüsselt?
- Welche Schwachstelle hat die Chiffre? Wie nutzt man sie aus, um die Chiffre zu brechen?
Normalerweise behandelt der Schulunterricht (aller Fächer) nur die Frage, wie etwas funktioniert. Dabei ist das Versagen eines Systems doch viel interessanter! Kryptografie bietet die Gelegenheit für einen entsprechenden Perspektivenwechsel: Beim Angriff auf eine Chiffre kann man auch einmal Fehler, Schwächen und Scheitern zum Gegenstand des Unterrichts machen. Das ist nicht nur für zukünftige Kryptologen lohnend.
Caesarchiffre (ca. 55 vor Chr.)
Die Verwendung dieser Chiffre durch Julius Caesar ist historisch verbürgt.
Verschlüsseln: Jeden Buchstaben des Klartextes verschiebt man im Alphabet um einen bestimmten Abstand nach hinten; diesen Abstand haben Absender und Empfänger vorher vereinbart und halten ihn geheim. Ein solches Geheimnis heißt →Schlüssel. Den resultierenden Buchstaben schreibt man in den Chiffretext1:

Den Chiffriervorgang kann man z.B. so aufschreiben:

Entschlüsseln: Der legitime Empfänger kennt den Schlüssel, macht die Verschiebung buchstabenweise rückgängig und erhält wieder den Klartext.
Schwachstelle und Angriff: Es gibt überhaupt nur 26 Verschiebungen des Alphabets; wenn man das unverschobene Alphabet beiseite lässt, hat die Caesar-Chiffre nur 25 mögliche Schlüssel.1 Man kann schlicht und einfach alle Schlüssel durchprobieren (in einer Klasse reicht es, wenn jeder Schüler eine Verschiebung testet) und bekommt früher oder später sinnvollen Klartext heraus. Diese Art Angriff heißt wegen des vollständigen Fehlens jedweder Raffinesse auch →brute-force-Angriff.
Schüler argumentieren hier (oder bei der Substitutionschiffre) oft, der Gegner könne diesen Angriff aber nur durchführen, wenn er schon weiß, dass es sich um eine Caesarchiffre handelt; so lange das verwendete System geheim ist, sei alles in Ordnung. Die Lehrperson sollte diese Gelegenheit unbedingt nutzen, das Kerckhoff'sche Prinzip zu erläutern.
Kerckhoff'sches Prinzip
Im Jahr 1883 formulierte Auguste Kerckhoff ein Grundprinzip der Kryptologie:2
In einem guten Kryptosystem muss nur der Schlüssel geheim bleiben.
Wer eine Chiffre oder ein anderes Kryptosystem erfindet oder einsetzt, sollte sich also nie darauf verlassen, dass dessen zugrundeliegenden Ideen, Algorithmen und Implementierungen geheim bleiben. Diese Hoffnung ist meistens trügerisch. Im militärischen Bereich ist das zumindest für taktische Kommunikation auch offensichtlich, denn früher oder später wird der Gegner natürlich Chiffriergeräte erbeuten und einen dafür ausgebildeten Funker gefangen nehmen. Der Versuch, ein System durch das Verschleiern seiner Funktionsweise sicher zu machen, heißt „security by obscurity“ und gilt unter Kryptografen als unseriös.
Dass man sich für die Sicherheit eines Systems nicht auf Geheimhaltung stützen soll, heißt andererseits nicht, dass man es unbedingt publizieren muss. Diese Entscheidung hängt auch davon ab, ob man auf die sorgfältige Analyse durch ein aufmerksames Fachpublikum und eine entsprechende Rückmeldung hoffen kann. Auch sicherheitsrelevante Teile eines Betriebssystems stehen ja buchstäblich jedem Nutzer zur Verfügung, lassen sich also nicht wirklich geheim halten (auch wenn ohne Programmquelltext ihre Analyse äußerst mühsam ist). Das Kerckhoff'sche Prinzip wird daher als Argument zugunsten von Open-Source-Software (OSS) verwendet. Allerdings zeigt die 2014 als „Heartbleed“ bekannt gewordene Sicherheitslücke in OpenSSL genau wie andere spektakuläre Fehler in OSS, dass die Fachwelt die Chance für eine gründliche Prüfung nicht immer nutzt.
Unstrittig ist aber die folgende Auslegung des Kerckhoff'schen Prinzips:
Je weniger Geheimnisse ein Kryptosystem braucht, desto robuster ist es.
Substitutionschiffre (ca. 800 n. Chr.)
Es gilt nun, einen brute-force-Angriff wie auf die Caesar-Chiffre auszuschließen. Das gelingt mit der Substitutionschiffre. Die Verwendung dieser Chiffre wird Karl dem Großen und Hildegard von Bingen nachgesagt3. Verschlüsseln: Das Alphabet wird nicht mehr rotiert, sondern „verwürfelt“. Jedem Buchstaben des Alphabets wird ein anderer Buchstabe zugeordnet; diese Zuordnung haben Absender und Empfänger vorher vereinbart und halten sie geheim.
Die obere Zeile lautet natürlich immer gleich und ist damit nicht geheim. Der Schlüssel besteht also aus der zweiten Zeile dieser Tabelle4. Weil für den ganzen Klartext ein einziges Ersetzungsalphabet verwendet wird, heißt eine solche Chiffren auch →monoalphabetisch. Die Cäsar-Chiffre stellt einen Spezialfall der monoalphabetischen Substitution dar.
Den Chiffriervorgang kann man z.B. so aufschreiben:

Entschlüsseln: Der legitime Empfänger kennt den Schlüssel, macht die Zuordnung buchstabenweise rückgängig und erhält wieder den Klartext.
Schwachstelle und Angriff: Widersteht diese Chiffre jetzt einem brute-force-Angriff? Wie viele denkbare Schlüssel hat die Substitutionschiffre?
Der Schlüssel ist eine Permutation des Alphabets, es gibt also 26! ≈ 4∙1026 verschiedene Schlüssel. Ausführlicher: Für den Schlüsselbuchstaben unter A gibt es 26 Möglichkeiten, einen Schlüsselbuchstaben auszuwählen, für den unter B nur noch 25 usw. Insgesamt gibt es also 26∙25∙24∙...∙2∙1=26! verschiedene Schlüssel.
Ist 26! genug?
Für diese Abschätzung denken wir uns den Angriff auf einer extrem schnellen, aber frei erfundenen Maschine. Einen solchen Rechner kann auch die NSA nicht bauen. Wie lange kann der brute-force-Angriff damit höchstens brauchen, wenn diese Maschine...:
- mit Spezialprozessoren arbeitet, die in jedem Takt einen Schlüssel testen können (also in einem Takt feststellen, ob es der richtige Schlüssel ist oder nicht);
- mit 10 GHz Taktfrequenz läuft, also jeder Prozessor zehn Milliarden Takte pro Sekunde ausführt;
- 100 solcher Prozessoren in jedem Serverschrank stecken hat;
- aus 100 solcher Schränke im Rechenzentrum der NSA besteht?
Sekunden? Minuten? Jahrtausende?
Es dauert höchstens 26! ≈ 4∙1026 Prozessortakte, bis die Maschine alle Schlüssel ausprobiert hat. Dafür braucht sie 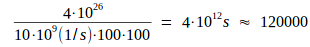 Jahre, im Mittel also 60000 Jahre.
Jahre, im Mittel also 60000 Jahre.
Dabei ist diese Maschine ja schon Utopie! Die Substitutionschiffre ist also immun gegen einen brute-force-Angriff. Lässt man die Schüler jetzt Schlussfolgerungen ziehen, bewerten viele sie als „unknackbar“. Das ist didaktisch gewollt, denn der gleiche Fehler ist auch in der Geschichte der Kryptografie immer wieder gemacht worden: „Mir fällt kein Angriff ein. Dann wird das System wohl sicher sein!“. Oder, wie es der Kryptologie-Experte Bruce Schneier ausdrückt: „Everybody can invent a cipher that he himself cannot break“.
Tatsächlich ist diese Chiffre sehr schwach.
Die Häufigkeiten der einzelnen Buchstaben bleiben auch nach der Substitutionschiffre erhalten. Abbildung 4 zeigt die Häufigkeitsverteilung der Buchstaben in deutschen Texten; das E als mit Abstand häufigster Buchstabe der deutschen Sprache sticht deutlich heraus. Im Beispiel von Seite 8 würde man es im Chiffretext als häufiges S wiederfinden.
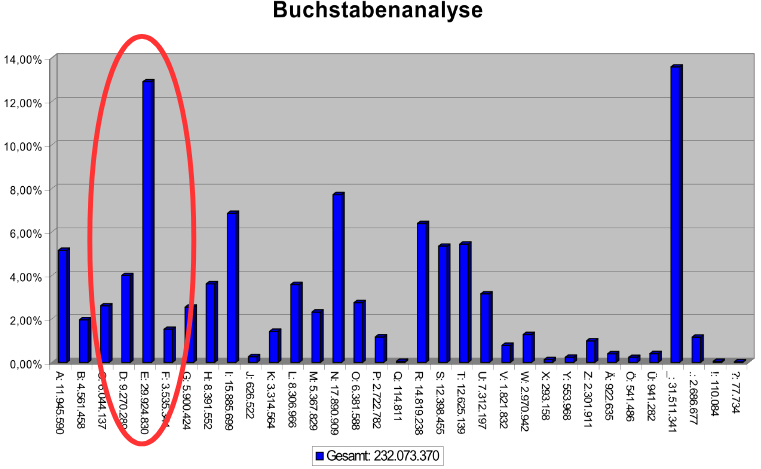
Abbildung 4: Buchstabenhäufigkeiten der deutschen Sprache, hier mit Umlauten, Leer- und Satzzeichen. Links sieht man deutlich das E, das im Deutschen stark heraussticht und sich bei einer monoalphabetischen Chiffre sofort verrät. Die nächsthäufigeren Buchstaben I, N, R, S, T unterscheiden sich aber kaum noch; man gewinnt sie stattdessen durch die Analyse von Buchstabenpaaren und -tripeln. Rechts sind Umlaute, Satz- und das auffällige Leerzeichen. Dieses lässt man bei der Verschlüsselung aber oft einfach weg.
Bild „Alphabet Häufigkeit“, Arbeitsgruppe EBUSS. URL: https://de.wikipedia.org/wiki/Datei:Alphabet_haufigkeit.svg (abgerufen: November 2016) [GNU-Lizenz für freie Dokumentation]
In Abbildung 4 fällt außerdem auch die Häufigkeit des Leerzeichens auf. Weil es nicht nur oft, sondern auch noch in charakteristischen Abständen auftritt, wäre es einfach zu identifizieren und würde dann sofort Rückschlüsse auf Wortlängen zulassen. Deswegen →normalisiert man bei allen klassischen Chiffren den Klartext vor dem Chiffrieren:
NAECHSTERANGRIFFZWEIUHRFUENFZEHN
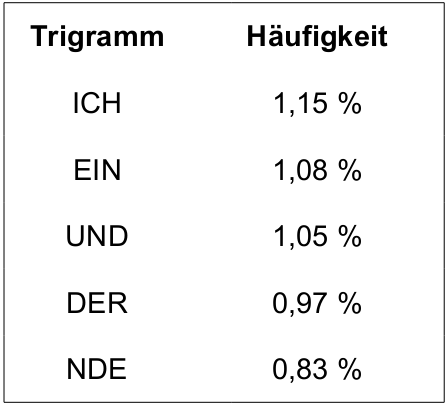
Abbildung 5: Die häufigsten Trigramme der deutschen Sprache
Siehe Seite „N-Gramm“. URL: https://de.wikipedia.org/wiki/N-Gramm (abgerufen: November 2016)
Außer dem E sind dann zwar keine weiteren Einzelbuchstaben sofort aus dem Histogramm ersichtlich; aber auch Buchstabenpaare und -tripel (→Digramme und →Trigramme) weisen in jeder Sprache charakteristische Häufigkeiten auf (Abb. 5). Falls der Chiffretext lang genug ist, erlaubt das einen einfachen und schnellen Angriff: Das schon bekannte E kommt in drei der häufigsten Trigramme vor und verrät damit auch die Chiffrebuchstaben zu N, I, D, U und R. Dazu kommen C und H. Wer etwas Übung mit Kreuzwort- und ähnlichen Rätseln hat, kann den Rest des Alphabets schnell erschließen.
Es gibt viele Spezialfälle der Substitutionschiffre. Man kann den Schlüssel etwa aus einem leicht zu merkenden Satz konstruieren, der den Anfang des Schlüssels bildet:
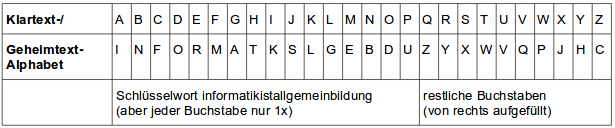
Solche Varianten sind natürlich nie schwieriger zu brechen als der allgemeine Fall der monoalphabetischen Substitution, meistens wird der Angriff sogar deutlich erleichtert: In diesem Fall konzentrieren sich etwa die selteneren Buchstaben im hinteren Teil des Schlüsselalphabets, und wer den Absender der Nachricht kennt, kann plausible Vermutungen darüber anstellen, welche Wörter im Schlüssel wohl auftauchen werden.
Homophone Chiffre
Die homophone Chiffre ist ebenfalls monoalphabetisch; sie verschleiert aber die charakteristischen Buchstabenhäufigkeiten, indem sie für häufigere Buchstaben mehrere Ersetzungszeichen vorsieht, aus denen beim Verschlüsseln gewählt werden kann.
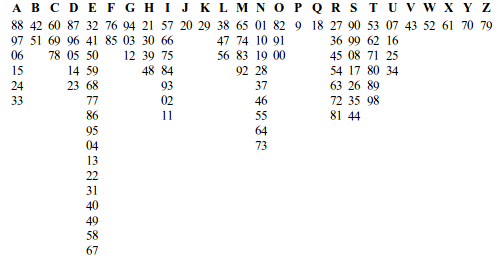
Abbildung 6: Ersetzung der Zeichen bei einer homophonen Chiffre. Ein Ziffernpaar steht jeweils für ein Symbol des Schlüsselalphabets. Für das im Deutschen mit 16% sehr häufige E gibt es 16 mögliche Ersetzungen, für Q nur eine.
Bild „Homophone Chiffren“, Marcel Brätz. URL: https://www.kryptographiespielplatz.de (abgerufen: November 2016)
Für den Angriff reichen Häufigkeiten allein dann nicht mehr aus. Er gelingt aber wieder über Buchstabengruppen: Die Tatsache beispielsweise, dass im Deutschen auf Q fast immer U folgt, zeigt sich auch im Kryptotext darin, dass nach der 18 fast immer 07, 16, 25 und 34 stehen, und zwar jeweils gleich häufig. Solche Muster erlauben das Brechen der Chiffre.
Vigenère-Chiffre (16.-19. Jahrhundert)
Um die einfache Häufigkeitsanalyse abzuwehren, entstanden polyalphabetische Systeme wie die Vigenère-Chiffre – sie galt sogar 300 Jahre lang als unangreifbar. Hier verwendet man für aufeinanderfolgende Buchstaben jeweils verschiedene Alphabete, so dass sich die Häufigkeiten der Buchstaben im Geheimtext weitgehend nivellieren.
Verschlüsseln: Alice und Bob haben ein Schlüsselwort k vereinbart, k=TOM. Alice schreibt es wiederholend unter ihren Klartext:

Nun wird das erste A mit dem Schlüsselalphabet T verschlüsselt (also wie mit einer Caesar-Scheibe in der Stellung „T unter A“5). Das U wird mit dem Alphabet O, das S mit M und das K wieder mit T verschlüsselt. Am einfachsten geht das mit dem Vigenère-Quadrat (vgl. Seite 23): Darin sucht man Schlüssel- bzw. Klartextbuchstabe an der linken bzw. oberen Achse und findet den zugehörigen Geheimtextbuchstaben im Inneren der Tabelle.

Die Häufigkeitsanalyse scheitert diesmal, weil jeder Klartextbuchstabe jetzt zu verschiedenen Geheimtextbuchstaben chiffriert wird (aus R beispielsweise wird K oder F oder D).
Entschlüsseln: Empfänger Bob schreibt den Schlüssel unter den Geheimtext und verfolgt die Buchstaben zurück: Er findet dabei (was vielen Schülern nicht gleich klar ist) den Geheimtextbuchstaben im Inneren der Tabelle, den Schlüssel auf der einen und den Klartext auf der anderen Achse.

Schwachstelle und Angriff: Die Chiffre hat zwar genügend mögliche Schlüssel, und sie ebnet die sprachtypische Häufigkeitsverteilung ein. Der Angriff gelingt stattdessen durch die Periodizität. Eve ermittelt zuerst die Schlüssellänge L und führt dann L-mal einen Caesar-Angriff durch, nämlich einen für jeden Buchstaben des Schlüsselwortes. Für den Unterricht kann man diese Reihenfolge aber umkehren. Oft finden Schüler die entscheidenden Ideen dann selber.
1. Man nimmt der Einfachheit halber an, die Schlüssellänge sei bekannt: L=3. Wie attackiert man dann den Geheimtext c= VRUJEGXEAVNGVBXEDXISILR?
Bei Schlüssellänge 3 ist jeder dritte Buchstabe mit demselben Schlüsselalphabet chiffriert worden: das V so wie das folgende J, das X usw. Allgemein wurden die Buchstaben an Position 1, 4, 7, 10 usw. auf die gleiche Weise chiffriert. Man könnte sie „Gruppe 1“ nennen. Das gleiche gilt natürlich auch für Position 2, 5, 8, 11 usw. („Gruppe 2“). Innerhalb jeder der drei Gruppen liegt ja lediglich eine Caesar-Chiffre vor. Man kann also gruppenweise Häufigkeiten zählen und auf diese Weise jede Gruppe einzeln angreifen. Zugunsten der Übersicht kann man die Gruppen getrennt aufschreiben:
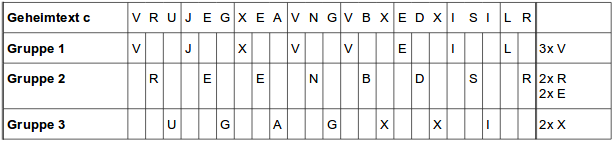
In Gruppe 1 ist das V sehr häufig, man vermutet dahinter ein E. Wenn das stimmt, müsste der erste Schlüsselbuchstabe R sein. Gruppe 3 führt analog auf T als Schlüssel. In Gruppe 2 sind E und R häufig, damit liegen A und N als Schlüsselbuchstabe am nächsten. Man kann einfach beide ausprobieren, oder man verwirft N, weil das auf den Wortanfang „EE“ führen würde, der im Deutschen normalerweise nicht vorkommt.
Der Schlüssel ist also RAT, der Klartext ERBSENGEHENNEBENDERSPUR.
2. Der nächste Schritt im Unterricht ist natürlich die Ermittlung der Schlüssellänge, die der Angreifer ja eigentlich noch nicht kennt. Für die Schule eignen sich Kasiski-Test, Autokorrelation und der partielle brute-force-Angriff.
Kasiski-Test zur Bestimmung der Schlüssellänge
Im folgenden Geheimtext fällt bei genauem Hinsehen die Folge HQQH auf:

Auch ohne Kenntnis des Klartextes liegt die Vermutung nahe, dass hier das gleiche Textfragment mehrfach verschlüsselt wurde, und zwar beide Male mit dem gleichen Teil des Schlüssels. HQQH tritt ab Position 8 und ein zweites Mal ab Position 23 auf. Wenn die Vermutung stimmt, muss der Abstand 23-8=15=3∙5 zwischen den Fragmenten also ein Vielfaches der Schlüssellänge sein, d.h. man vermutet L=3 oder L=5 oder L=15. Wenn andere Zeichenfolgen ebenfalls mehrfach auftreten, kann man auf diese Weise die Schlüssellänge schnell eingrenzen – und mit dem oben beschrieben Angriff weitermachen.
Das obige Beispiel wurde natürlich passend vorbereitet, aber in längeren Texten passiert das tatsächlich auch von selbst, vor allem mit häufigen →Di- und →Trigrammen.
Autokorrelation zur Bestimmung der Schlüssellänge
Die Autokorrelationsmethode lässt sich besonders gut automatisieren. „Von Hand“ ist sie zwar etwas mühsamer als der Kasiski-Test; dafür funktioniert sie aber auch bei Texten, die gar keine sich wiederholenden Buchstabenfolgen enthalten.
Die Vigenère-Chiffre ebnet zwar die Häufigkeitsunterschiede zwischen den Gruppen ein, aber innerhalb einer Gruppe sind immer die gleichen Buchstaben häufig (bzw. selten). Das nutzt man aus, indem man den Geheimtext buchstabenweise verschiebt und seine Übereinstimmungen mit sich selber zählt. Wenn nach der richtigen Verschiebung (nämlich um genau eine Schlüssellänge) alle Buchstaben wieder mit denen ihrer eigenen Gruppe zusammentreffen, fällt das bei der Zählung sofort auf:

Die sechs Treffer bei Verschiebung drei stechen hier deutlich heraus, die nächsten Maxima treten erwartungsgemäß bei Verschiebung 6 und 9 auf (mit nachlassender Tendenz wegen abnehmender Überlappung der beiden Texte): Die Schlüssellänge ist offensichtlich 3. Diese Zählung kann man Schüler sehr gut mit Papierstreifen machen lassen. Danach können viele auch mit eigenen Worten begründen, warum eine Autokorrelation die Schlüssellänge aufdeckt.
Partieller brute-force-Angriff zur Bestimmung der Schlüssellänge
Da Vigenère bei bekannter Schlüssellänge so einfach zu brechen ist, kann man den Angriff auch einfach mit allen möglichen Schlüssellängen durchführen. Sobald man die richtige Länge rät, fällt das anhand der statistischen Eigenschaften der Buchstabengruppen sofort auf. Es handelt sich also um einen brute-force-Angriff nur auf einen Teil des Schlüssels. Das Vorgehen ist deswegen interessant, weil ein vollständiger brute-force-Angriff auf den gesamten Schlüssel zu aufwändig wäre; der zweiteilige Angriff (nämlich die Länge des Schlüssels per brute-force, danach seinen Inhalt auf die oben besprochene Weise zu ermitteln) ist hingegen absolut realistisch.6 Auch dieser Angriff ist übrigens leicht zu automatisieren.
Die Vigenère-Chiffre ist damit vollständig gebrochen. Geschichtlich markieren die Angriffe auf Vigenère den Wandel der Kryptologie (vor allem der Kryptoanalyse) von einer linguistisch zu einer mathematisch geprägten Disziplin. Der amerikanische Kryptologe William Frederick Friedman entwarf um 1920 sogar einen Angriff auf die Schlüssellänge, in den (neben statistischen Eigenschaften der Klartextsprache) nur die Auszählung der Buchstabenhäufigkeiten im Chiffretext eingeht7.
Transpositionschiffre
Bei Transpositionschiffren bleiben die Zeichen einer Botschaft unverändert erhalten, werden stattdessen aber umsortiert. Diese Chiffren bilden damit eine zweite Klasse neben den Substitutionen, bei denen jedes Klartextzeichen am Platz bleibt und dort durch ein anderes ersetzt („substituiert“) wird.8
Ein einfaches Beispiel hierzu ist die „Gartenzauntransposition“:
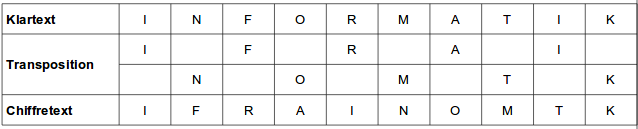
Beispiele für diese Verschlüsselungsklasse sind Skytale, Fleißnersche Schablone oder auch →ADFGX.
One-Time-Pad (OTP, ca. 1880)
Beim hier vorgeschlagenen Unterrichtsgang markiert das One-Time-Pad einen charmanten Wendepunkt in der Unterrichtseinheit: Nachdem die Schüler sich gerade daran gewöhnt haben, dass nun mal jede Chiffre früher oder später gebrochen wird, halten sie die „unknackbare“ für ein Hirngespinst. Unknackbare Chiffren gibt es aber.
Für die Begründung dieser bemerkenswerten Eigenschaft verwenden wir den Begriff „Information“ wie in der Informationstheorie, aber auf informelle Weise und qualitativ: Er bedeutet hier „Ausschluss von Möglichkeiten“. Eine Chiffre nennen wir dann „perfekt sicher“, wenn Eve durch das Abfangen der Nachricht keinerlei Information gewinnen kann.
Beispiel: Die Aussage „Jemand in Deutschland hat letzten Mittwoch im Lotto gewonnen.“ lässt etwa 80 Mio. Möglichkeiten, wer das sein könnte. Jede Einschränkung dieser Möglichkeiten betrachten wir als Informationszuwachs.
- Die Aussage „Rüdiger Obermüller aus Offenburg war's“ schränkt die Auswahl auf eine einzige Person ein – mehr Information kann man nicht bekommen.
- Die Aussage „Die Gewinnerin ist weiblich, über 80 Jahre alt und hat mindestens Schuhgröße 44“ schränkt die Anzahl der Kandidat(inn)en drastisch ein – der Informationsgewinn ist immer noch sehr groß.
- Die Aussage „Die Person ist älter als 9 Jahre“ verringert den Kreis der möglichen Gewinner um immerhin 8.000.000 Menschen und stellt damit einen geringen Informationsgewinn dar.
- Die Aussage „Ich war es leider nicht“ schließt nur eine Person aus, 79999999 bleiben übrig. Der Informationsgewinn ist winzig.
Betrachten wir die Substitutionschiffre noch einmal aus dieser Perspektive und beschränken uns auf Klartexte mit elf Buchstaben. Wenn wir wissen, dass es sich um eine Substitutionschiffre handelt (wir erinnern uns ans Kerckhoff'sche Prinzip: Über dieses Wissen verfügt der Angreifer immer) – hilft uns der Geheimtext dann, Möglichkeiten (also Klartexte) auszuschließen? Anders gefragt: Welcher elfbuchstabige Klartext ist hier nicht verschlüsselt worden?

Auch die Klartexte FRUEHSTUECK, KRYPTOGRAPH, CHIFFRIEREN oder INTELLIGENT kommen wegen ähnlicher Konflikte nicht in Frage. Der Angreifer kann viele Klartexte ausschließen, nachdem er den Geheimtext abgefangen hat. Vielleicht kann er sogar den echten Klartext ermitteln. Jedenfalls verschafft die Kenntnis des Geheimtextes ihm einen gewissen Informationsgewinn im oben beschriebenen Sinn. Entscheidend ist, dass dieser Zugewinn durch das Abfangen der Nachricht entsteht.
Auch für die Caesar-Chiffre konstruiert man leicht einen Geheimtext und sieht, dass man mit seiner Hilfe Klartexte ausschließen kann. Bei Caesar reicht dafür schon eine kurze Nachricht mit nur wenigen Buchstaben – deswegen ist Caesar ja so schwach.
Eine perfekt sichere Chiffre muss also folgende Eigenschaft haben: Auch nachdem Eve den Geheimtext abgefangen hat, kommt für sie immer noch jeder Klartext in Frage9 (der passende Länge hat).
Das One-Time-Pad hat tatsächlich diese Eigenschaft.
Schlüsselerzeugung: Der Schlüssel muss
- absolut zufällig gewählt werden,
- mindestens so lang sein wie die Nachricht
- und natürlich geheim bleiben.
Im Unterricht kann man OTP-Schlüssel z.B. mit einem Alphabet aus Scrabble-Steinen erzeugen, die man verdeckt aus einer Tasche zieht. Man zieht mindestens so viele Buchstaben, wie man später chiffrieren möchte.
Verschlüsseln: Genau wie bei Vigenère schreibt man Schlüssel und Klartext untereinander und benutzt das Vigenère-Verfahren. Namensgebend ist insbesondere die Tatsache, dass der so erzeugte Schlüssel auch...
- nur ein einziges Mal verwendet werden darf.
Den nicht benutzten Teil des Schlüssels kann man für die nächste Nachricht aufheben oder wegwerfen. Den benutzten Teil muss man wegwerfen.
Entschlüsseln: Genau wie bei Vigenère schreibt man Schlüssel und Geheimtext untereinander und benutzt die Vigenère-Tabelle.
Warum ist OTP nun perfekt sicher?
Auch mit dem Wissen c=GSSPZDF kann Eve keinen einzigen (siebenbuchstabigen) Klartext ausschließen. Anders gesagt: Sie kann zu jedem hypothetischen Klartext m' auch einen Schlüssel k' angeben, der aus diesem m' den Chiffretext c=GSSPZDF gemacht hätte, und dieses k' ist genauso wahrscheinlich wie alle anderen auch. Sie muss also alle m' nach wie vor in Betracht ziehen. Eve erfährt daher nichts Neues über m (was sie nicht auch schon vor dem Abfangen der Nachricht wusste).
Aber der Superrechner der NSA kann es doch bestimmt mit brute force?! Brute force liefert eine Liste aller Klartexte (mit passender Länge) – und kein einziger sticht irgendwie heraus. Man hat nichts gewonnen. Es gibt eben keine Angriffe auf OTP, nicht heute und nicht morgen. Sie können auch nicht erfunden werden. Weder schnellere Maschinen noch Quantencomputer können OTP angreifen. Wenn die Information im Chiffretext gar nicht drinsteckt – dann kann auch kein Verfahren sie herausholen.
OTP ist perfekt sicher. Prima! Dann waren ja alle kryptografischen Probleme schon 1880 gelöst. Aber woran arbeiten Kryptografen dann überhaupt? OTP ist zwar sehr einfach und sehr sicher, wirft aber in der praktischen Anwendung massive Probleme auf.
Problem des →Schlüsselaustauschs: Wenn man genau so viel Schlüsselmaterial braucht, wie auch die Nachricht lang ist, und der Schlüssel auf einem sicheren Weg übermittelt werden muss – dann könnte man darüber ja auch gleich die Nachricht selber verschicken.
Problem der Schlüsselverwaltung: Das komplette OTP-Schlüsselmaterial muss nicht nur erzeugt und übergeben, sondern anschließend bis zur Verwendung auch sicher aufbewahrt werden. Das ist in vielen Szenarien („Geheimagent in Feindesland“) gar nicht machbar.
Auch die mangelnde Robustheit von OTP ist problematisch: Es bietet perfekte Sicherheit – bei richtiger Durchführung. Aber schon bei kleinsten Fehlern in der Handhabung stürzt OTP wie ein Kartenhaus in sich zusammen. Das ist im Alltag gefährlich, und zwar nicht nur wenn Laien die Chiffre einsetzen.
Obwohl das One-Time-Pad für die meisten Anwendungen unpraktisch ist, wurde und wird es tatsächlich eingesetzt, wenn einerseits Geld keine Rolle spielt und andererseits Schlüsselverteilung und -verwaltung logistisch machbar sind. Das war beispielsweise beim „Heißen Draht“ zwischen Moskau und Washington der Fall: Diese Fernschreibverbindung sollte im Kalten Krieg verhindern, dass aufgrund von Missverständnissen Raketen starten. Auch im Zweiten Weltkrieg war die Weitergabe gebrochener Enigma-Funksprüche von Bletchley Park nach London zwar sehr eilig; noch wichtiger war den Briten aber die absolute Geheimhaltung ihres Einbruchs in Enigma. Ein OTP leistet beides.
Beide Szenarien (Kalter Krieg und Bletchley) erlauben den Einsatz von OTP, weil der vorherige Austausch ausreichender Mengen Schlüsselmaterial „auf Vorrat“ ohne weiteres durchführbar war. In beiden Fällen vereinfacht auch die Punkt-zu-Punkt-Verbindung die Schlüsselverteilung (im Vergleich zu einem Kommunikationsnetz).
Viele andere Kryptosysteme ahmen die Idee nach, indem sie aus einem kurzen Schlüssel einen langen, unregelmäßigen, aber eben nur pseudozufälligen „Schlüsselstrom“ erzeugen, mit dem dann der Klartext chiffriert wird; auch Enigma ist dafür ein Beispiel. Die Sicherheit eines One-Time-Pad erreicht man damit aber nicht.
Enigma
Die Chiffriermaschine Enigma10 wurde von den Zwanzigerjahren bis 1945 vom deutschen Militär verwendet. Trotz regelmäßiger Verbesserungen vor allem während des Krieges gelangen den Alliierten immer wieder Einbrüche in die Chiffre; letztlich konnten deutsche Enigma-Funksprüche nahezu kontinuierlich entziffert werden, was den Krieg vermutlich um Jahre verkürzt hat.
Obwohl das Thema sehr spannend ist und im Unterricht auch gut ankommt, wird hier auf Details verzichtet. Eine ausgezeichnete Darstellung findet sich bei swisseduc.ch11, auch sehr gute Simulatoren sind leicht verfügbar12.
Moderne symmetrische Chiffren: DES, AES und ihre Anwendung
Nach der Einführung asymmetrischer Verfahren (siehe unten) entsteht oft die Fehlvorstellung, symmetrische Verfahren seien nun überflüssig oder zu schwach, asymmetrische hingegen neu und sicher. Ganz im Gegenteil sind starke symmetrische Verfahren auch bei sehr modernen Anwendungen wie etwa SSL/TLS prinzipiell unverzichtbar.
Symmetrische Chiffren sind auch in aktuellen Anwendungen weit verbreitet. Für Clouds oder verschlüsselte Container auf eigenen Speichermedien ist beispielsweise kein aufwändiger Schlüsselaustausch nötig, wenn nur eine Person oder eine kleine Gruppe darauf zugreift.
Symmetrische Chiffren wie DES und AES werden für viele moderne Anwendungen eingesetzt. Das Portal inf-schule.de bietet hierzu (wie für viele weitere Themen) Material und Aufgaben.
Inf-schule.de: AES – Ein moderndes symmetrisches Chiffrierverfahren.
Didaktischer Hinweis: Es bietet sich an, eine praktische Einheit etwa mit VeraCrypt anzuschließen. Derzeit (Frühjahr 2016) ist VeraCrypt das einzige Kryptocontainer-Werkzeug, das Open Source ist, als hinreichend sicher gilt und unter Linux, MacOS und Windows gleichermaßen komfortabel funktioniert. Daran können Schüler ganz konkret erleben, wie Kryptografie mit wenig Aufwand und geringer Einarbeitung ihren Alltag erleichtert. Da sich die Tools und ihre Handhabung immer wieder ändern, wird hier auf fertige Arbeitsblätter und Ablaufbeschreibungen verzichtet. Unter http://lehrerfortbildung-bw.de/werkstatt/sicherheit/stickcrypt/vc/ können Sie derzeit Unterlagen zu VeraCrypt abrufen.
Aus demselben Grund sollte auch bei einer praktischen Einheit Wert darauf gelegt werden, die kryptografischen Fachkonzepte wiederzuerkennen und zu benennen: Warum ist für diese Anwendung eine symmetrische Chiffre sinnvoll? Warum ein starkes Passwort? Warum muss man beim Schlüsselerzeugen in VeraCrypt „so komisch an der Maus wackeln“? Die Erzeugung der Zufallszahlen aus der Mausbewegung ist eine gute Gelegenheit, über vom Rechner erzeugte Pseudozufallszahlen und ihren Einfluss auf die Sicherheit eines Kryptosystems zu sprechen.
1 Caesar soll zusätzlich die Buchstaben ins griechische Alphabet übertragen haben. Weil dabei kein Geheimnis (kein Schlüssel) benötigt wird, handelt es sich aber im kryptografischen Sinn nicht um eine Chiffre, sondern eine Codierung (hier im Sinne einer Geheimschrift).
2 Den Schlüssel 0 wollen Schüler intuitiv ausschließen, obwohl er zumindest für sehr kurze Klartexte (mit einem oder zwei Buchstaben) nicht unsicherer ist als andere. Dieser Überlegung gehen wir auf Seite 15 nach.
3 Siehe Seite „Geschichte der Kryptographie“. URL:https://de.wikipedia.org/wiki/Geschichte_der_Kryptographie (abgerufen: November 2016) – verweist auf Friedrich L. Bauer: Entzifferte Geheimnisse. 3., überarbeitete und erweiterte Auflage. Springer, 2000, ISBN 3-540-67931-6
4 Der Schlüssel im Beispiel wurde durch verdecktes Ziehen (ohne Zurücklegen) von Scrabble-Steinen erzeugt. Dabei wurde zuvor von jedem Buchstaben genau ein Stein in den Sack gelegt. Nun wird hier ein Buchstabe (das T) auf sich selbst abgebildet. Ist das schlimm? Sollte man es korrigieren? Den ganzen Schlüssel verwerfen? Oder wenigstens das T neu ziehen? Schüler plädieren oft für eine Korrektur, „weil der Schlüssel sonst nicht zufällig genug“ sei. Tatsächlich würde das Verwerfen vermeintlich „unzufälliger“ Schlüssel das System aber sogar schwächen, weil dann weniger Möglichkeiten bleiben. Und (Kerckhoff'sches Prinzip!) der Gegner weiß ja, ob wir Schlüssel verwerfen, die uns nicht gefallen, und wenn ja, welche. Der gleiche Fehler unterlief im zweiten Weltkrieg auch den Deutschen bei der Erzeugung von Enigma-Schlüsseln: Keine Walze durfte am nächsten Tag wieder an der gleichen Stelle stecken, weil das als „unzufällig“ angesehen wurde. Dieser Handhabungsfehler erleichterte (wie viele andere) den Briten auch tatsächlich den Angriff auf Enigma.
5 Methodischer Hinweis: Die Lehrperson muss nicht unbedingt formulieren, dass hier „wie mit Caesar“ gearbeitet wird. Manche Schüler bemerken das auch selbst, insbesondere wenn sie die Chiffre dann brechen sollen. Spätestens für den Angriff sollte diese Einsicht aber bei allen vorhanden sein.
6 Durch ein vergleichbares Vorgehen gelang dem polnischen Team um Marian Rejewski schon Mitte der 30er Jahre ein Einbruch in die deutsche Chiffre Enigma: Auch Enigma hatte einen zweiteiligen Schlüssel, und es gelang Rejewski, die beiden Teile getrennt anzugreifen. Für den ersten Teil ließ Rejewski bestimmte Eigenschaften von ca. 100000 Einstellungen vorausberechnen (das dauerte etwa ein Jahr), der zweite war ein Spezialfall einer Substitutionschiffre. Rejewski legte damit den Grundstein für die späteren britischen Erfolge gegen Enigma.
7 Siehe Seite „Friedman-Test“. URL: https://de.wikipedia.org/wiki/Friedman-Test (abgerufen: November 2016)
8 Siehe Seite „Transposition (Kryptographie)“. URL: https://de.wikipedia.org/wiki/Transposition_(Kryptographie) (abgerufen: November 2016)
9 Dabei darf Eve durchaus wissen, dass bestimmte Nachrichten vorkommen können und andere nicht, oder dass ANGRIFFIMMORGENGRAUEN im Moment plausibler ist als HABLUSTAUFPIZZAFUNGHI – aber das wusste sie ja auch schon vor dem Abfangen der Nachricht. Entscheidend ist, dass sie danach keine zusätzliche Information hat.
10 Siehe Seite „Enigma_(Maschine)“. URL: https://de.wikipedia.org/wiki/Enigma_(Maschine) (abgerufen: November 2016)
11 Siehe Seite „Einigma Dokumentation“. URL: http://www.swisseduc.ch/informatik/daten/kryptologie_geschichte /docs/enigma_dokumentation.pdf (abgerufen: November 2016)
12 Siehe Seite „Universal Enigma“. URL: https://people.physik.hu-berlin.de/~palloks/js/enigma/enigma-u_v20.html Siehe Seite „Enigmasimulator 7.0“. URL: http://users.telenet.be/d.rijmenants/en/enigmasim.htm (abgerufen: November 2016)
Hintergrund: Kryptographie: Herunterladen [odt][408 KB]
Hintergrund: Kryptographie: Herunterladen [pdf][379 KB]
Weiter zu Asymmetrische Chiffren
