Eine Muster-Rechenaufgabe
Infobox
Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Bitte beachten Sie, dass der Bildungsplan fortgeschrieben wurde.
Aufgabe:
Ein PKW fährt mit 90 km/h. Plötzlich erblickt die Fahrerin ein Hindernis. Nach einer Schrecksekunde macht sie eine Vollbremsung und kommt nach 100 m zum Stehen. Diese 100 m Anhalteweg beinhalten die Strecke, die in der Schrecksekunde zurückgelegt wird, und den eigentlichen Bremsweg.
- Wie groß ist die Verzögerung (also die negative Beschleunigung) bei der Vollbremsung?
- Wie lange dauert der gesamte, oben beschriebene Vorgang?
- Angenommen, der Abstand zwischen PKW und Hindernis hätte zum Zeitpunkt des Erblickens nur 80 m betragen. Mit welcher Geschwindigkeit wäre der PKW auf das Hindernis geprallt?
- Wie groß hätte die Verzögerung des PKW mindestens sein müssen, um den Zusammenprall zu vermeiden?
-
Wie schnell hätte Fahrerin maximal fahren dürfen, um den Zusammenprall zu vermeiden?
(Rechnen Sie mit der Verzögerung aus Teil a!)
Lösung a:
Während der Schrecksekunde (Index s) zurückgelegter Weg:
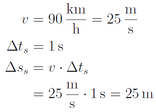
Der Anhalteweg beträgt 100 m. Da 25 m in der Schrecksekunde zurückgelegt wurden, bleiben noch 75 m für den Bremsweg (Index b) übrig. Die Fahrerin muss also in 75 m von 25 m/s auf 0 m/s herunterbremsen. Gesucht ist dafür die Verzögerung a .
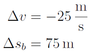
Die Formel Δ s b = ½· a ·(Δ t b ) 2 nützt zunächst nichts, da Δ t b unbekannt ist. Also muss man zunächst die Bremszeit Δ t b bestimmen. Die beiden Formeln Δ s b = ½· a ·(Δ t b ) 2 und Δ v = a ·Δ t b zusammen helfen aber weiter: Löst man die zweite Formel nach a auf und setzt sie in die erste Formel ein, so erhält man
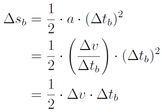
Dies kann man nach Δ t b auflösen:
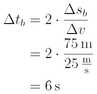
Die Bremszeit beträgt also 6 s. Nun lässt sich die Verzögerung berechnen:
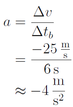
Die Verzögerung des PKW beträgt also ca. -4 m/s 2 .
Lösung b:
Die Gesamtzeit ist die Summe aus Schrecksekunde und Bremszeit:
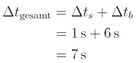
Der gesamte Vorgang dauert 7 s.
Lösung c:
Eigentlich braucht die Fahrerin 100 m, um zum Stillstand zu kommen. Sie hat jetzt aber nur 80 m Platz. Gesucht ist also die Geschwindigkeit, die sie 20 m vor dem Stillstand noch hat. Man kann sich die Arbeit erleichtern, indem man umgekehrt denkt: Welche Geschwindigkeit hat ein PKW nach 20 m, der aus der Ruhe heraus mit +4 m/s 2 beschleunigt. Dazu braucht man erst wieder die Zeit:
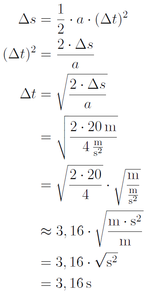
Nun muss die Geschwindigkeit nach 3,16 s berechnet werden:
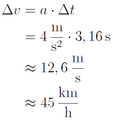
Der PKW fährt mit einer Geschwindigkeit von 45 km/h auf das Hindernis auf!
Lösung d:
Man verwendet dieselbe Vorgehensweise wie in Aufgabenteil a - allerdings mit einem kürzeren Bremsweg: 80 m (Abstand zum Hindernis) minus 25 m (Weg in der Schrecksekunde). Die Fahrerin muss also in 55 m von 25 m/s auf 0 m/s herunterbremsen. Gesucht ist dafür die Verzögerung a .
Berechnung der Bremszeit Δ t (Herleitung der Formel wie in Aufgabenteil a):
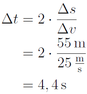
Nun lässt sich die Verzögerung berechnen:
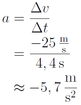
Die Verzögerung des PKW hätte also -5,7 m/s 2 betragen müssen, um den Zusammenprall zu verhindern.
Lösung e:
Der Anhalteweg setzt sich aus Weg Δ s s in der Schrecksekunde und Bremsweg Δ s b zusammen:
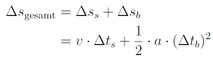
Die Bremszeit Δ t b ergibt sich wieder aus der Gleichung v = a ·Δ t b , die man nach Δ t b auflöst. Setzt man dies ein, so erhält man:
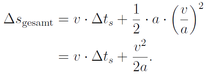
Dies ist eine quadratische Gleichung für v, was man leicht erkennen kann, wenn man die Summanden umsortiert:
Die Gleichung kann man mit der Mitternachtsformel lösen:
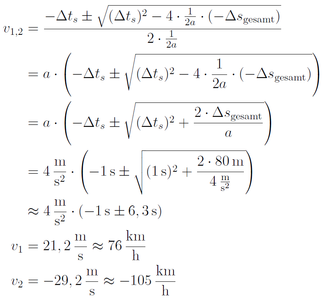
Nur die Lösung v1 ist physikalisch sinnvoll.
Die Fahrerin hätte also maximal mit einer Geschwindigkeit von 76 km/h fahren dürfen.
Aufgabe 9:Versuchen Sie, die Musteraufgabe selbst zu rechnen! |
