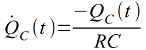Entladevorgang Kondensator — mit Modellbildung

Bezug zum Bildungsplan

2. Physik als theoriegeleitete Erfahrungswissenschaft

1. Die SuS können die naturwissenschaftliche Arbeitsweise Hypothese, Vorhersage, Überprüfung im Experiment, Bewertung, ... anwenden und reflektieren.
2. Die SuS können ein Modell erstellen, mit einer geeigneten Software bearbeiten und die berechneten Ergebnisse reflektieren.

4. Spezifisches Methodenrepertoire der Physik

1. Die SuS können Zusammenhänge zwischen physikalischen Größen untersuchen.
2. Die SuS können Experimente unter Anleitung planen, durchführen, auswerten, grafisch veranschaulichen und einfache Fehlerbetrachtungen vornehmen.
3. Die SuS können computerunterstützte Messwerterfassungs- und Auswertungssysteme im Praktikum selbstständig einsetzen.

8. Grundlegende physikalische Größen

Die SuS können mit weiteren grundlegenden physikalischen Größen umgehen: elektrische Stromstärke, elektrische Spannung, elektrische Ladung, Kapazität.

Unterrichtlicher Zusammenhang

Nachdem die grundlegenden Kenngrößen des Kondensators im Unterricht behandelt wurden, soll zunächst der Entladevorgang eines Kondensators untersucht, interpretiert und anschließend mit einem Modell nachgebildet werden. Die Theorie dazu wird im Unterricht besprochen oder durch angemessene Lektüre erarbeitet.

Problemstellung

In Blitzlichtgeräten werden Kondensatoren aufgeladen und dann beim Auslösen entladen. Dabei stellen sie Energie zur Verfügung, die eine Lampe in Licht umsetzt.

Ziel

Durch eigenes Experimentieren lernen Sie die Besonderheiten beim Entladen eines Kondensators kennen. Sie gewinnen dabei mehr Sicherheit im Experimentieren mit CASSY und lernen außerdem CASSY Lab als Modellbildungssystem zu nutzen.

Aufgabenstellung

Untersuchen Sie den Entladevorgang eines Kondensators und bilden Sie ihn in einem geeigneten Modell nach.

Geräte

1	Kondensator 47 µF (578 38)
1	Widerstand 10 kΩ (577 07)
1	Umschalter
1	Schüler-Experimentiernetzgerät
1	Stecksystem
1	Pocket-CASSY (524 006) mit USB-Kabel mit 1 UIP-Sensor S (524 0621)
1	PC oder Laptop

Durchführung

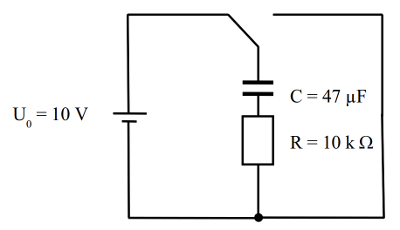
1. Zeit-Spannungs-Kennlinie eines Kondensators
   1. Bauen Sie eine Schaltung zum Auf- und Entladen eines Kondensators mit einem Umschalter auf.

      

      Achten Sie bei Verwendung eines Elektrolytkondensators auf die richtige Polung!
   2. Schließen Sie das Messwerterfassungssystem so an, dass Sie die Spannung am Kondensator messen können.
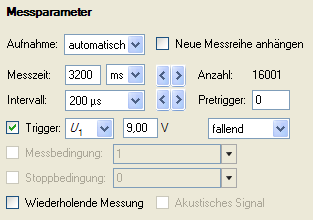
   3. Nehmen Sie in CASSY Lab die notwendigen Einstellungen vor, um die t-U-Kennlinie messen zu können. Die Messung soll automatisch starten, wenn die Spannung am Kondensator beim Entladen 9,0 V erreicht hat. (Tipp: Trigger einstellen!)
2. Modellbildung
   1. Vorbereitung der Modellbildung
      1. Unter Einstellungen den Zweig Rechner wählen und dort Parameter bzw. Formel auswählen.
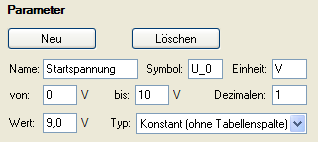
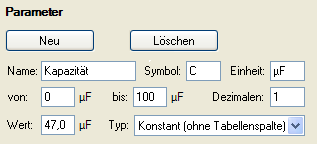
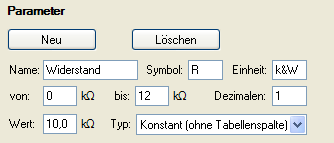
      2. Folgende Parameter Neu eingeben bzw. Größen mit Formel n definieren:
         

         Kapazität und Widerstand sind Konstanten, die von den verwendeten Geräten abhängen. Sie können während des Versuchsablaufs verändert werden.

         

         

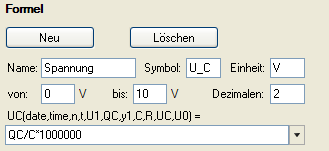
         Die Spannung U _C (t) = Q⋅C(t)/C ist die momentan am Kondensator anliegende Spannung.

         

         Die Startspannung U ₀ sei die Spannung bei Beginn der Messung des Entladevorganges und kann individuell festgelegt werden.

         

   2. Modellbildung

      Die Modellbildung erfolgt durch Eingabe der Differenzialgleichung für die Ladung beim Entladevorgang:

      

      

      Vorgehen:

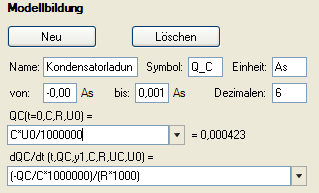
      1. Neues Modell wählen.
      2. Ladung Q_C definieren, Wertebereich festlegen.
      3. Anfangswert für Q _C (t = 0 s) eingeben: C*U0/1000000
      4. Differenzialgleichung eingeben: (-QC/C*1000000)/(R*1000)
         Hinweis: Die Faktoren kommen zustande, da die Kapazität C in μF und der Widerstand in kΩ eingegeben wurden.
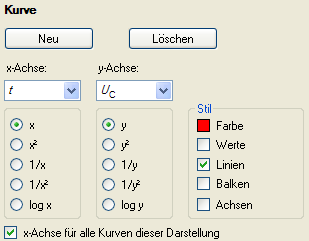
   3. Darstellung für Diagramm auswählen

      

   4. Messparameter anzeigen und eingeben

      

Erneute Durchführung des Versuches:

Mit oder F9. Die Kurve aus der Modellbildung wird automatisch mitgezeichnet.

Zusatzaufgaben:

Führen Sie den Versuch mit anderen Widerständen oder mit Kondensatoren anderer Kapazität durch. Machen Sie Vorhersagen über den Verlauf der Kennlinien.

Auswertung

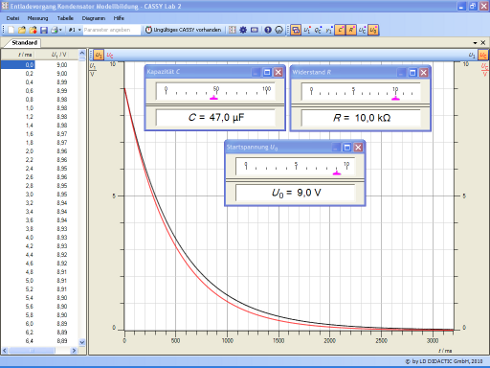
1. Zeit-Spannungs-Kennlinie des Kondensators und Modellkurve
   1. Interpretieren Sie den Verlauf der entstandenen Kennlinien. Finden Sie Gemeinsamkeiten und Unterschiede zwischen Modell und Realexperiment.
   2. Durch Verschieben der jeweiligen Schieberegler für Kapazität, Widerstand und Startspannung kann die Modellbildungskurve der Messkurve angenähert werden. Welche Einflüsse haben Kapazität, Widerstand und Startspannung auf den Entladevorgang?
   3. Regeln Sie so, dass Modell und Experiment gut übereinstimmen. Begründen Sie die Abweichungen zwischen Modell und Experiment!
2. Halbwertszeit des Kondensators
   1. Was versteht man unter der Halbwertszeit des Entladevorgangs?
   2. Bestimmen Sie die Halbwertszeit für den von Ihnen verwendeten Kondensator aus dem Experiment!
   3. In der Literatur findet man für die Halbwertszeit eines Kondensators folgende Gleichung: T _H  = R⋅C⋅ln2 ≈ 0,69⋅R⋅C. Vergleichen Sie mit dem experimentellen Ergebnis.
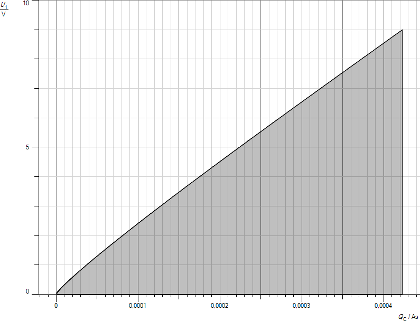
3. Energie des elektrischen Feldes
   1. Der Kondensator ist Speicher von Energie. Wie lässt sich die Energie eines Kondensators berechnen?
   2. Ermitteln Sie die im elektrischen Feld des von Ihnen verwendeten Kondensators gespeicherte Energie durch Rechnung!
   3. Überprüfen Sie das Ergebnis mit den experimentellen Werten! (Hinweis: Die Software CASSY-Lab ermittelt einen negativen Wert für die Fläche unter der Ursprungsgeraden. Das liegt in der Art der internen Integration und kommt zustande, da die Werte für U und Q beim Entladen abnehmen.)

      

Versuchsbeispiel:

Aufbau:

Download

Entladevorgang Kondensator Modellbildung: Herunterladen [doc] [2,9 MB]

 

Weiter mit Cassy 2: Induktion bei rotierendem Magneten