Dialog Fahrrad am Hang

Dialog von Lisa und Tom Fahrrad am Hang

(Die Schaubilder wurden mit dem CAS-Rechner Voyage 200 von Texas Instruments erstellt.)

Vormittag

Tom: Schau mal, ich habe Eric gefilmt, wie er mit dem Fahrrad den Hang herunterrollt.
Lisa: Und was willst du damit?
Tom: Ich will das Gesetz herausfinden, das für diese Bewegung gilt!
Lisa: Ah ja …
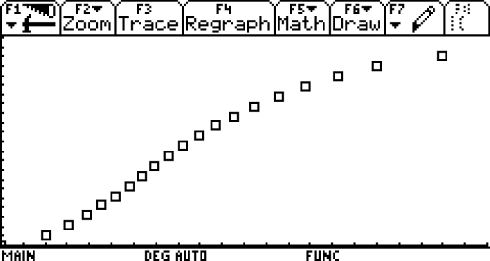
Tom: An Hand der Aufnahme kann ich sehr genau feststellen, zu welchen Zeitpunkten Eric die Wegmarken passierte. Hier siehst du das Zeit-Weg Diagramm. Ein Teilstrich auf der Rechtsachse bedeutet 3 s, ein Teilstrich auf der Hochachse 10 m.

Jetzt bin ich dabei die Funktion zu suchen, die am besten zu den Messwerten passt. Mir scheint, dass ich dafür mindestens eine Funktion dritten Grades brauche.
Lisa: Weil das Schaubild einen Wendepunkt hat?
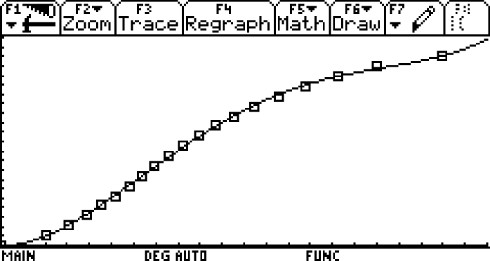
Tom: Ja genau, … Warte mal, … die Übereinstimmung der Daten mit den Werten der Regressionskurve dritten Grades ist mir nicht gut genug. Ich probiere noch eine Kurve vierten Grades aus. Ah, das sieht doch prima aus!

Hier sind Gleichung und zugehörige Kurve:
s(t) = 5,12⋅10 ^-5 x ⁴ - 7,42⋅10 ^-3 x ³ + 3,15⋅10 ^-1 x ² - 7,54⋅10 ^-2 x - 2,41⋅10 ^-1
Jetzt kann ich zu jedem Zeitpunkt die entsprechende Wegmarke angeben. Ich weiß, wann Eric bei einer gegebenen Stelle war, ich kann mit der Ableitung die Geschwindigkeitsfunktion bestimmen, ebenso die Beschleunigungen, … ich weiß alles über die Bewegung!
Genau so macht man das in der Forschung auch. Das ist wissenschaftliche Arbeitsweise! Galilei hat diese Methode als Erster verwendet. Aus seinen Messungen hat er die Fallgesetze abgeleitet!
Lisa: Ehrlich?
Tom: Ja klar, das habe ich in der Schule gelernt.
Lisa: Sag mal, was nutzt dir das eigentlich?
Tom: Hey, das habe ich doch schon gesagt!
Lisa: Ich will ja nicht bezweifeln, dass deine Formel die Bewegung ziemlich gut wiedergibt. Dennoch kannst du nicht abstreiten, dass deine Zahlen mit Messfehlern behaftet sind. Wie willst du dann sicher sein, dass deine Formel das korrekte Gesetz für die Bewegung ist?
Tom: Meine Formel ist doch genau so ermittelt, dass die Abweichungen zu den Messpunkten minimal sind!
Lisa: Aber Potenzfunktionen höherer Ordnung könnten noch besser sein. Die hast du gar nicht ausprobiert!
Tom: Warum sollen wir die Sache unnötig kompliziert machen? Unter konkurrierenden Lösungen ist die Einfachste die Beste! Das hat - glaube ich - Einstein gesagt. Na also.
Lisa: Hmmm, … Eric kommt mit seinem Fahrrad zum Schluss doch zum Stehen?
Tom: Ja sicher, irgendwann ist er so langsam, dass das Fahrrad kippt.
Lisa: Dann ist die Kurve im Diagramm zum Schluss waagrecht?
Tom: Worauf willst du hinaus?
Lisa: Deine Kurve steigt zum Schluss wieder an und zudem hat eine Potenzfunktion höheren Grades niemals ein Schaubild, das zum Schluss waagrecht ist. Das schaffst du vielleicht mit einer Exponentialfunktion, so ähnlich wie beim beschränkten Wachstum. Dein Gesetz kann deshalb nicht korrekt sein!
Tom: Uff, wo hast du denn das gelernt?
Lisa: Auch in der Schule, wo denn sonst?
Tom: Na ja, ich dachte vielleicht hat dein Physikerpapa …
Okay, dann ändere ich die Formel eben um … oder ich lasse diesen Teil des Vorgangs weg. Es ist schließlich völlig unerheblich, wie lang Eric zum Schluss dasteht.
Lisa: Langsam, langsam. Selbst wenn du eine Exponentialfunktion gefunden hast, die eine perfekte Ausgleichskurve durch deine Messpunkte liefert, so gilt sie doch nur für diesen speziellen Vorgang. Rollt ein anderer Fahrradfahrer oder ein Leiterwagen oder ein Ball den Hang hinunter, dann nützt sie dir gar nichts. Jeder Vorgang hat seine eigene mathematische Modellierung, d.h. bei jedem Beispiel kannst du wieder von vorn anfangen mit der Aufnahme von Messwerten und der Erstellung von Formeln. Dein Gesetz ist nicht verallgemeinerbar und deshalb ist es auch kein Gesetz.
Tom: Du bist ja nicht gerade sehr schmeichelhaft zu mir. Welches Gesetz beschreibt denn deiner Meinung nach diese Radfahrt?
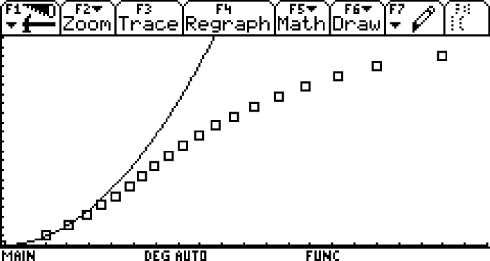
Lisa: Fürs Erste würde ich annehmen, dass es sich um eine Bewegung mit konstanter Beschleunigung handelt. Wenn g die Erdbeschleunigung und α der Neigungswinkel des Hangs ist, gilt: a = g⋅sinα und s=½⋅a⋅t ² . Die Steigung der Strecke schätze ich auf 5 %, damit erhalte ich s(t) = 0,245 m/s ²  ⋅ t ² . Das Schaubild sieht so aus:

Tom: Bist du mit der Übereinstimmung deiner Theorie mit meiner Messung zufrieden?
Lisa: Na ja, meine Beschreibung trifft nur für den ersten Abschnitt der Bewegung zu und da liegt die Kurve doch ganz gut! Die Abweichungen sind unvermeidlich, schließlich habe ich den Vorgang nur idealisiert betrachtet. Den zweiten Abschnitt muss man separat behandeln.
Tom: Ha! Du kannst den Vorgang auch nicht einheitlich beschreiben und musst Abweichungen in Kauf nehmen. Das ist interessant! Die Situation ist also die:
Ich habe eine Spezialformel, die die Messdaten perfekt wiedergibt, leider aber nicht auf andere Vorgänge anwendbar ist. Du hast ein einfaches Modell, das vielen Vorgängen zu Grunde liegt, leider aber in seiner Reinform kaum jemals in der wirklichen Erfahrung vorkommt. Das ist wohl die Kluft zwischen Theorie und Praxis!
Lisa: Um eine bessere Beschreibung zu bekommen müssen wir die Reibung berücksichtigen. Die Masse des Gefährts spielt meiner Meinung nach keine Rolle.
Tom: Das sind vor allem Luft- und Rollreibung. Die sind dafür verantwortlich, dass verschiedene Fahrradfahrer unterschiedlich rollen. Jetzt wird es aber kompliziert.
Lisa: Ich kann ja zwischendurch meinen Vater fragen.

Nachmittag

Lisa: Für die Luftreibung spielt natürlich die Form des Gefährts und die Geschwindigkeit eine Rolle. Bei kleinen Geschwindigkeiten ist der Luftwiderstand eher proportional zur Geschwindigkeit v, bei höheren Geschwindigkeiten kann er aber auch proportional zu v ² werden.
Tom: Wie sollen wir denn bei solchen Komplikationen noch eine Zeit-Weg Prognose fabrizieren?
Lisa: Erst mal kommt noch die Rollreibung ins Spiel. Die wird eventuell sogar von der Masse beeinflusst …
Mein Vater meint aber, wir sollen uns deshalb keine zu großen Sorgen machen. Mit Hilfe von Differenzialgleichungen könne man noch einiges zu Stande bringen und wenn das Netz von Beziehungen sehr kompliziert wird, gäbe es nummerische Verfahren.
Tom: Und dann hat man die exakte Lösung? Eine Zeit-Weg Funktion, die den speziellen Vorgang beschreibt und aus allgemeinen Prinzipien abgeleitet ist?
Lisa: Er sagt, wenn man die Beschreibung noch weiter verbessern möchte, müsste man auch den Drehimpuls der Räder berücksichtigen.
Tom: Langsam glaube ich, dass es immer noch weitere Komplikationen gibt und dass das Verfeinern unserer Beschreibung überhaupt kein Ende nimmt. Was meinst du?
Lisa: … Tja … Bestimmt gibt es jemand, der zu diesem Thema auch einmal etwas Sinniges gesagt hat.

Download

Dialog Fahrrad am Hang: Herunterladen [doc] [92 KB]

 

Weiter mit Hinweise und Lösungen