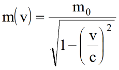Beispiele

Schaltung von Kondensatoren
Selbstständige Erarbeitung

Ziel: Sie sollen dem Schulbuch möglichst effizient einen Sachverhalt entnehmen, ihn verstehen und anwenden.

Frage:

Welche Kapazität erhält man, wenn man mehrere Kondensatoren zusammenschaltet?

Aufgabe:

1. Suchen Sie im Schulbuch das entsprechende Kapitel.
2. Entnehmen Sie dem Kapitel die zugehörigen Gleichungen. Überlesen Sie zunächst die Herleitungen und versuchen Sie so schnell wie möglich eine Antwort auf die gestellte Frage zu finden.
3. Machen Sie sich klar, was die Gleichungen aussagen.
4. Erstellen Sie einen möglichst kurzen und prägnanten Heftaufschrieb. Beschränken Sie sich wie bei einem Spicker auf das Allerwichtigste.

Kontrolle: Überprüfen Sie, ob Sie alles richtig verstanden haben.

5. Welcher Satz ist richtig:
   1. Bei der Parallelschaltung von Kondensatoren ist die Ersatzkapazität
      1. größer als die größte Einzelkapazität
      2. größer als die kleinste Einzelkapazität
      3. kleiner als die kleinste Einzelkapazität
   2. Bei der Reihenschaltung von Kondensatoren ist die Ersatzkapazität
      1. kleiner als die größte Einzelkapazität
      2. kleiner als die kleinste Einzelkapazität
      3. größer als die kleinste Einzelkapazität
6. Schalten Sie drei Kondensatoren mit einer Kapazität von je 1 μF auf möglichst viele verschiedene Arten zusammen und berechnen Sie jeweils die Ersatzkapazität

Ergänzung: Wenn Sie neugierig geworden sind, können Sie sich nun auch die Herleitungen der Gleichungen anschauen.

Geschwindigkeitsabhängigkeit der Masse
Planarbeit

Problemstellung:

Eine Konsequenz der speziellen Relativitätstheorie ist, dass die Masse eines jeden Körpers von seiner Geschwindigkeit abhängt.

Ist m ₀ die Ruhemasse eines Körpers (v = 0) und bewegt sich der Körper mit der Geschwindigkeit v an uns vorbei, so messen wir eine Masse von

c = 3⋅10 ⁸  m/s = 300000 km/s ist die Lichtgeschwindigkeit.

Fragen:

• Was bedeutet diese Formel anschaulich?
• Wie sieht das Schaubild dieser Funktion aus?
• Wieso ist uns dieser Effekt noch nie aufgefallen? Ab welcher Geschwindigkeit spielt die relativistische Massenzunahme etwa eine Rolle?
• Welche Konsequenzen kann man daraus ziehen?

Aufgaben:

Klären Sie diese Fragen mit IhremTaschenrechner TI 83 mit möglichst wenig Hilfestellung.

Tipp: Setzen Sie m ₀  = 1 Masseneinheit. Ersetzen Sie in der Gleichung den Quotienten v/c durch eine Variable. Sie gibt den Anteil der Geschwindigkeit von der Lichtgeschwindigkeit an.

Hilfestellung:

1. Führen Sie einen System - RESET durch:
   • 2nd MEM 5 1 2
2. Definieren Sie die Funktion:
   • Y= Y 1 =1/(1-X 2 ) ½ ENTER 2nd QUIT
3. Betrachten Sie das Schaubild:
   • Schaubild definieren
     • WINDOW X min  = 0 X max  = 1 X scl  = 0,1 Y min  = 0 Y max  = 10
   • Schaubilder betrachten
4. Betrachten Sie die Funktionswerte in der Tabelle:
   • Tabelle definieren
     • 2nd TBLSET TblStart = 0 ENTER ΔTbl = 0.01 ENTER 2nd QUIT
   • Tabellenwerte betrachten
     • 2nd TABLE
     • GRAPH

Energie und Energiedichte des magnetischen Feldes
Planarbeit

Problemstellung:

Aus dem Ausschaltvorgang bei einer Spule konnte geschlossen werden, dass in ihrem magnetischen Feld Energie gespeichert ist. Wie lässt sich diese Energie berechnen?

Ziele:

• Für alle:
  • Eine Gleichung zur Berechnung der Energie im Feld einer stromdurchflossenen Spule kennen, verstehen und anwenden können.
  • Die Gleichung für die Energiedichte kennen, verstehen und anwenden können.
• Für Schüler, sie sich mehr zutrauen:
  • Die Gleichung für die Energiedichte einer schlanken Spule herleiten können.
• Für Schüler, die sich viel mehr zutrauen:
  • Die Gleichung für die Energie des magnetischen Feldes einer stromdurchflossenen Spule herleiten können.

Hilfsmittel:

Buch Dorn-Bader S. 70, 71

Zeit:

1 Schulstunde plus häusliche Arbeitszeit

Zur Vorbereitung:

Noch ohne Buch , auf dem Schmierblatt!

• Von welchen Größen wird die Energie des magnetischen Feldes einer stromdurchflossenen Spule abhängen?
• Von welchen Größen wird die Energiedichte des magnetischen Feldes abhängen?
• Betrachten Sie die entsprechenden Gleichungen für das elektrische Feld und versuchen Sie, Gleichungen für den magnetischen Fall zu erraten. Einheitenkontrolle!

Aufgaben

Entscheiden Sie, welche der genannten Ziele Sie erreichen möchten. Entnehmen Sie die entsprechenden Informationen dem Lehrtext im Buch und erstellen Sie damit IHREN Heftaufschrieb.

Kontrollfragen

Überprüfen Sie Ihre Lernziele. Wie viele Aufgaben Sie bearbeiten, hängt davon ab, was Sie sich vorgenommen haben. (Buch Dorn-Bader)

Aufgabe 1

Buch S. 71: A1 {18 J; 15,3 J; 36,7 m; 233}

Aufgabe 2

Buch S. 71: A2 {6,3 mH; 0,31 J}

Aufgabe 3

Schreiben Sie die gelernten Gleichungen auswendig auf. Was bedeuten die einzelnen Größen in der Gleichung?

Aufgabe 4

Beschreiben und erklären Sie die Bilder auf S. 71 in B2 mit eigenen Worten.

Aufgabe 5

Erklären Sie eine der Herleitungen, die Sie sich vorgenommen haben, Ihrem Partner auf einem zunächst leeren Blatt Papier.

Download

Unbekannte Formeln im Unterricht: Herunterladen [doc] [64 KB]