Hinweise und Lösungen

Hinweise und Lösungen zum Arbeitsblatt Modelle und ihre Eigenschaften

1. Schauen Sie sich die beiden Videos Fahrradfahrt am Hang - Beobachterperspektive und Fahrradfahrt am Hang - Blick auf den Tacho an.

   Schauen Sie sich die beiden Videos Fahrradfahrt am Hang - Beobachterperspektive und Fahrradfahrt am Hang - Blick auf den Tacho an.

   Quelle: DVD in den Handreichungen zum Lehrbuch Cornelsen, Physik Oberstufe Bestellnummer: 013007; die Clips sind nicht auf der DVD im Schülerbuch enthalten!

2. In dieser Aufgabe sollen sich die Schüler mit dem im Videoclip gezeigten Sachverhalt vertraut machen und die Gedanken von Lisa und Tom nachvollziehen. Bei Zeitknappheit kann man diesen Vorspann auch überspringen und sofort die Aufgaben 3 und 4 bearbeiten.

   Lesen Sie den Dialog von Lisa und Tom und bearbeiten Sie folgende Aufträge:

   1. Einen Vorgang zu beschreiben und ihn zu erklären sind zwei verschiedene Dinge.
      Beschreiben Sie die Bewegung des Fahrrads.

      Das Fahrrad beschleunigt bis zu einer gewissen Höchstgeschwindigkeit. Diese ist bei 70 m erreicht, dort geht das Gefälle in eine horizontale Strecke über. Ab hier wird das Fahrrad verzögert, bis es jenseits von 190 m zum Stillstand kommt.

      Erklären Sie den Bewegungsablauf.

      Beschleunigende Kräfte sind die Komponente der Gewichtskraft, die längs der geneigten Strecke zeigt sowie die Kräfte, die durch Luft- und Rollwiderstand entstehen. Die Resultierende führt zu einer Beschleunigung, die nicht unbedingt konstant ist, da der Luftwiderstand von der Geschwindigkeit abhängt. Ab der Wegmarke 70 m wirken nur noch die bremsenden Kräfte, deshalb verlangsamt sich die Bewegung bis zum Stillstand.

   2. Lisa teilt den Vorgang in Abschnitte ein. Erläutern Sie, was damit gemeint ist.

      Im ersten Abschnitt wird das Fahrrad schneller, im zweiten Abschnitt wird es langsamer und kommt zum Stillstand. Im dritten Abschnitt ruht es.

   3. Erklären Sie, wie Lisa auf die Formel s(t) = 0,245 m/s ²  ⋅ t ² kommt.

      Mit tan α = 0,05 folgt α = 2,86°. Aus a = g⋅sin α ergibt sich a = 0,49 m/s ² . Damit ist s = 1/2⋅a⋅t ²  = 0,245 m/s ² ⋅t ² .

   4. Die Tabelle zeigt die aus dem Video ermittelten Messdaten.
      

      Zeit in s	0	6,08	9,2	11,7	13,8	15,8	17,6	19,3	21,1	23,0	...
      Weg in m	0	10	20	30	40	50	60	70	80	90	...

      ...	25,0	27,2	29,5	32,0	34,9	38,2	41,8	46,2	51,8	60,8
      ...	100	110	120	130	140	150	160	170	180	190

      Ermitteln Sie mit Ihrem GTR eine Regressionskurve dritter Ordnung für die Messdaten.

      s(t) = - 1,28⋅10 ^-3 x ³ + 8,32 x ² - 2,83 x - 7,28

      Warum ist Tom mit dieser Kurve noch nicht zufrieden?

      Bei t = 0 sind Wegmarke s und Geschwindigkeit v deutlich von Null verschieden. Die Kurve liegt zunächst über den Messpunkten und anschließend umgekehrt.

3. In dieser Aufgabe setzen sich die Schüler mit Eigenschaften naturwissenschaftlicher Modelle auseinander.

   Bei ihrer Untersuchung modellieren Tom und Lisa die Fahrradfahrt am Hang.

   In der Tabelle sind Eigenschaften naturwissenschaftlicher Modelle aufgelistet.

   (Die Tabelle findet man in ähnlicher Form in: Cornelsen, Physik Kursstufe Bad.-Württ., Best. Nr.: 130375, Seite 402 bzw. in Cornelsen; Physik Oberstufe, Gesamtband; Nr.: 130061; S. 528)

   Nennen Sie - mit Bezug auf den Dialog - für jede Eigenschaft ein Beispiel.

   Eigenschaft	Beispiel im Dialog
   Ein Modell vereinfacht oder idealisiert das Phänomen. Das Phänomen wird auf Aspekte reduziert, die für den Verwendungszweck relevant sind.	Lisa reduziert die Betrachtung zunächst auf den ersten Teil der Bewegung. Sie vereinfacht und idealisiert, indem sie eine Bewegung mit konstanter Beschleunigung unterstellt. Tom reduziert den Vorgang zunächst auf eine reine Weg-Zeit Analyse.
   Ein Modell beruht auf Vorstellungen und Gesetzen mit deren Hilfe das Phänomen erklärbar und verstehbar wird.	Bei ihrem ersten Modell nimmt Lisa an, die Bewegung erfolge mit konstanter Beschleunigung, wobei diese aus g und α berechnet wird. Damit kann sie den Verlauf der Kurve ein Stück weit erklären.
   Ein Modell ermöglicht Prognosen. Es kann den Ablauf eines realen Vorgangs voraussagen.	Sowohl Toms Regressionsformel als auch Lisas Vorschläge ermöglichen Prognosen z.B. für den Verlauf der Bewegung zwischen den Messpunkten, aber auch für die Geschwindigkeit und Beschleunigung.
   Ein Modell hat seine Grenzen. Diese zeigen sich z.B. im Vergleich der Prognosen mit den experimentellen Befunden.	Lisa und Tom können mit ihren Modellen nicht alle Aspekte der Fahrradbewegung berücksichtigen. Ihre prognostizierten Zeit-Weg Kurven weichen deshalb mehr oder weniger von den Messdaten ab. Es gibt viele Aspekte, die nicht erfasst werden: wie tief der Boden von den Reifen eingedrückt wird, die Größe der Räder, Windböen, …
   Das Erkennen der Grenzen eines Modells regt zur Suche nach verbesserten Modellen an. So wird Erkenntnisfortschritt möglich.	Lisa und Tom verbessern ihre Modelle immer mehr, indem sie weitere Aspekte wie Luftreibung, Rollreibung, Drehimpuls der Räder, … hinzunehmen. Hierzu sind weitere Informationen und ggf. Experimente nötig.
   Ein Modell ist umso bedeutungsvoller, auf je mehr Phänomene es anwendbar und je einfacher es ist.	Toms mathematisches Modell ist physikalisch praktisch bedeutungslos. Je mehr Aspekte die Modelle berücksichtigen, desto komplizierter werden sie.

Nachdem der Modellbegriff durch seine Eigenschaften charakterisiert ist, sollen die Schüler sich mit der Rolle von Modellen im Erkenntnisgewinnungsprozess auseinandersetzen.

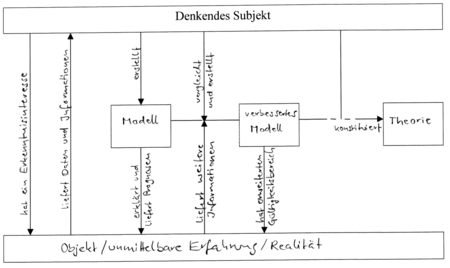
Das Begriffsnetz soll die Vermittlerrolle physikalischer Modelle im Erkenntnisgewinnungsprozess darstellen.

Zur Auswahl stehen zwölf Satzteile. Beschriften Sie damit sowohl die Rechtecke als auch die Pfeile sinnvoll:

liefert Daten und Informationen	Objekt/unmittelbare Erfahrung/Realität
Theorie	liefert weitere Informationen
hat erweiterten Gültigkeitsbereich	vergleicht und erstellt
erklärt und liefert Prognosen	Modell
verbessertes Modell	konstituiert
hat ein Erkenntnisinteresse	erstellt

Download

Hinweise und Lösungen: Herunterladen [doc] [182 KB]

Weiter mit Weitere Aufgaben