Freie Enthalpie bei Redoxreaktionen
Infobox
Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Bitte beachten Sie, dass der Bildungsplan fortgeschrieben wurde.
Die Energieumsätze verschieden kombinierter Redoxpaare erklären, weshalb immer die unedleren Metalle in Lösung gehen. Gleichzeitig scheidet sich das jeweils edlere Metall aus der Metallsalzlösung auf dem unedleren Metall ab.
Beispiel: 2 Ag
+
(aq) + Zn(s) → 2 Ag + Zn
2+
(aq) | Δ G = ?
Das folgende Schema zeigt, dass sowohl das Auflösen eines festen Metalls als auch das Abscheiden eines Metalls aus der Lösung über drei Teilschritte erfolgt:
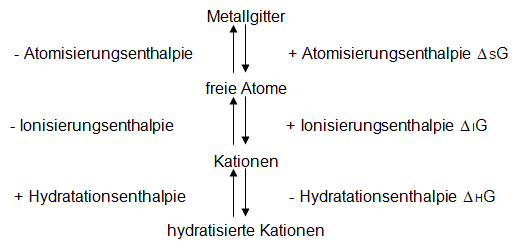
Mit Hilfe der molaren freien Standardenthalpien der drei Teilschritte der Redoxpaare lassen sich die Energieumsätze einzelner Redoxreaktionen näherungsweise berechnen, siehe Tabelle.
|
Redoxpaar |
Δ A G 0 m [kJ·mol -1 ] |
Δ I G 0 m [kJ·mol -1 ] |
Δ H G 0 m [kJ·mol -1 ] |
| Ag/Ag + |
247
|
738
|
- 478
|
| Al/Al 3 + |
284
|
5146
|
- 4615
|
| Au/Au + |
305
|
893
|
606
|
| 2 Br - /Br 2 |
82
|
- 337
|
- 337
|
| Ca/Ca 2+ |
143
|
1740
|
- 1592
|
| 2 Cl - /Cl 2 |
106
|
- 359
|
- 313
|
| Cu/Cu 2+ |
300
|
2708
|
- 2080
|
| Fe/Fe 2+ |
358
|
2326
|
- 1910
|
| H 2 /2 H + |
203
|
1314
|
- 1089
|
| Hg/Hg 2+ |
32
|
2821
|
- 1824
|
| 2 I - /I2 |
70
|
- 307
|
- 247
|
| K/K + |
61
|
421
|
- 336
|
| Li/Li + |
128
|
522
|
- 510
|
| Mg/Mg 2+ |
114
|
2193
|
- 1905
|
| Na/Na + |
78
|
498
|
- 410
|
| Pb/Pb 2+ |
101
|
2170
|
- 1496
|
| Sn/Sn 2+ |
268
|
2125
|
- 1556
|
| Zn/Zn 2+ |
95
|
2643
|
- 2025
|
Molare freie Standardenthalpien für Atomisierung Δ A G 0 m , Ionisierung Δ I G 0 m und Hydratation Δ H G 0 m .
Freie Enthalpie bei Redoxreaktionen: Herunterladen [doc] [43 KB]
Freie Enthalpie bei Redoxreaktionen: Herunterladen [pdf] [123 KB]
