Zur Hauptnavigation springen [Alt]+[0] Zum Seiteninhalt springen [Alt]+[1]

Kegelschnitte / Schülermaterialien

Arbeitsaufträge und Fragestellungen ...

Untersuchung einer Konstruktion auf ihre Eigenschaften


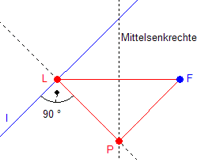
Station Parabel
Gegeben ist eine Gerade l und ein Punkt F, der nicht auf der Geraden l liegt.

  1. Gegeben ist zusätzlich ein Punkt L, der auf der Geraden l liegt. Welche Eigenschaften hat das Dreieck LQF? Versuche deine Vermutungen zu begründen.
  2. Was kannst du über den Abstand von P zu der Geraden l und dem Punkt F sagen?
  3. Konstruiere einen Punkt P der von der Geraden l und dem Punkt F den gleichen Abstand hat.
Parabel Eigenschaften einer Konstruktion
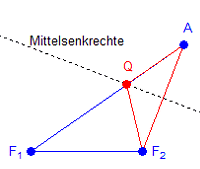
Station Ellipse
Gegeben sind die Punkte F 1 und F 2 , deren Abstand 3 cm beträgt. Die Strecke F 1 A ist 5 cm lang.
  1. Welche Eigenschaften hat das Dreieck F 2 QA? Versuche deine Vermutungen zu begründen.

  2. Welche Eigenschaft hat die Summe der Abstände des Punktes Q zu den beiden Punkten F 1 und F 2 ? Begründe deine Aussage
  3. Konstruiere einen Punkt P, dessen Summe der Abstände zu F 1 und zu F 2 5 cm ist.
Ellipse Eigenschaften einer Konstruktion
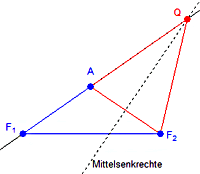
Station Hyperbel
Gegeben sind die Punkte F 1 und F 2 , deren Abstand 5 cm beträgt. Die Strecke F 1 A ist 3 cm lang.
  1. Welche Eigenschaften hat das Dreieck F 2 AQ? Versuche deine Vermutungen zu begründen.

  2. Wie erhältst du die Streckenlänge der Strecke F 1 A aus den beiden Abständen des Punktes Q zu den Punkten F 1 und F 2
  3. Konstruiere einen Punkt P, so dass die Differenz der Abstände des Punktes P zu den Punkten F 1 und F 2 3 cm beträgt.

Hyperbel Eigenschaften einer Konstruktion
Download der Arbeitsaufträge mit Konstruktionsvorlagen [zip/html/doc/Dynageo][36 KB]

Konstruktion der Ortslinie und ihre Eigenschaften

Die Arbeitsaufträge für die Expertengruppen Parabel, Ellipse und Hyperbel sind als Worddateien abgelegt. Die Lösungen der Konstruktion finden Sie als html-Dateien abgespeichert. Überlegen Sie, welche Hilfen sie Ihren Schülerinnen und Schülern geben möchten und ob Sie Programmteile vorgeben möchten.

Download der Materialien für die Expertengruppen und Lösungen [zip/word/html/Dynageo][82 KB]

Bemerkungen zu dem Programm Euklid-DynaGeo

Informationen zu dem Programm Euklid-DynaGeo finden Sie auf der Seite von Roland Mechlin:
EuklidDynaGeo von Roland Mechling  

Sollten Sie das Programm nicht haben, können Sie die html-Dateien anschauen, müssen aber zulassen, dass eine ActivX-Komponente geladen wird, damit der DynaGeoX-Viewer geladen wird. Informationen zum DynaGeoX-Viewer finden Sie unter der Seite EuklidDynaGeo von Roland Mechling   , dann weiter zu Galerie. Unter "Technische Voraussetzungen" finden Sie Hinweise und Hilfen zur Installation und Update des DynaGeoX-Viewers.
Sollten Sie ActiveX-Komponenten nicht zulassen wollen oder sollte DynaGeo auf Ihrem Rechner nicht laufen, können Sie hier die wichtigsten Screenshots finden.