Kegelschnitte
Kurzinformation
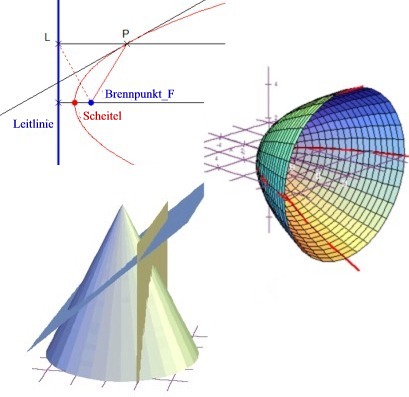
Kegelschnitte werden heute im Mathematikunterricht selten behandelt. Die dynamischen Geometrieprogramme erlauben eine Behandlung der Kegelschnitte als Ortslinien in der Sekundarstufe I. Für die Konstruktion und Eigenschaften der Kegelschnittskurven wird nur Wissen über Mittelsenkrechte, Winkelsumme in Dreiecken und Winkel an Parallelen gebraucht. So lernen die Schülerinnen und Schüler komplexere Ortslinien zu den bekannten wie z.B- Kreis oder Mittelsenkrechte. Durch den Praxisbezug können Schülerinnen und Schüler die Bedeutung der Mathematik an einem Beispiel erfahren.
Die Lösung der Aufgabe erfordert vernetztes mathematisches Denken. Da die mathematische Aufgabenstellung und ihre Lösung für die einzelnen Kegelschnitte sehr ähnlich sind, eignet sich dieses Thema für einen Lernzirkel und ein Gruppenpuzzle.
| Fach: | Mathematik |
| Thema der Einheit: | Kegelschnitte als Ortslinie |
| Zielgruppe: | Sekundarstufe I |
| Zeitrahmen: | ca. 7 Stunden |
| Grundfragen: | Welche Ortslinien erhält man bei speziellen Abstandsfragen? Welche Eigenschaften haben diese Ortslinien? |
| Aufwand: | mittel |
| Digitale Medien: |
Hardware:
Software:
|
| Schlagworte: | Kegelschnitte, Ortslinie, Abstand, Mittelsenkrechte, Winkelsumme in Dreiecken, Winkel an Parallelen |
| Autor: |
Ingeborg Tuffner-Denker:
|
| Unterrichtspraxis: | Unterrichtsdokumentation |
| Vorbereitungsraum: | Lernpfad |
